位相シフトフルブリッジコンバータ(Phase Shift Full Bridge略してPSFB)を勉強しよう!という記事の1回目です。

1回目:【電源回路】位相シフトフルブリッジコンバータ(PSFB)の動作原理(本記事)
2回目:【電源回路】位相シフトフルブリッジコンバータ(PSFB)はなぜソフトスイッチングするのか?
3回目:【電源回路】位相シフトフルブリッジコンバータ(PSFB)のデューティーサイクルロスについて
本日は位相シフトフルブリッジコンバータの動作原理を解説してみようと思います。
・位相シフトって何?PWM制御とどう違うの?
・出力電圧はどう決まるの?
ということをお悩みの方の参考になれば幸いです。どういう動作をしてどういう理屈で出力電圧が決まるのか?を考えてきます。
ちなみにPWM制御フルブリッジコンバータの動作原理をこちらで書いておりますので、良かったら読んでみて下さい。
位相シフトフルブリッジコンバータの出力電圧計算式
最初に結論です。出力電圧は以下の式で計算できます。
$$\small{
V_{out}=\frac{n_2}{n_1}V_{in}α\\
α=\frac{T_1}{T_1-T_2}
}$$
Vout:出力電圧[V]
Vin:入力電圧[V]
n1:変圧器の1次側巻き線数
n2:変圧器の2次側巻き線数
α:位相シフトの割合
T1:モード1(Q1,Q4=ONの時間)[sec]
T2:モード2(Q1,Q3=ONの時間)[sec]
α?T1,2?モード1?モード2?って何?について説明していきます。
そもそも位相シフトとは?
PWM制御はスイッチのON幅を制御して出力電圧を決めます。
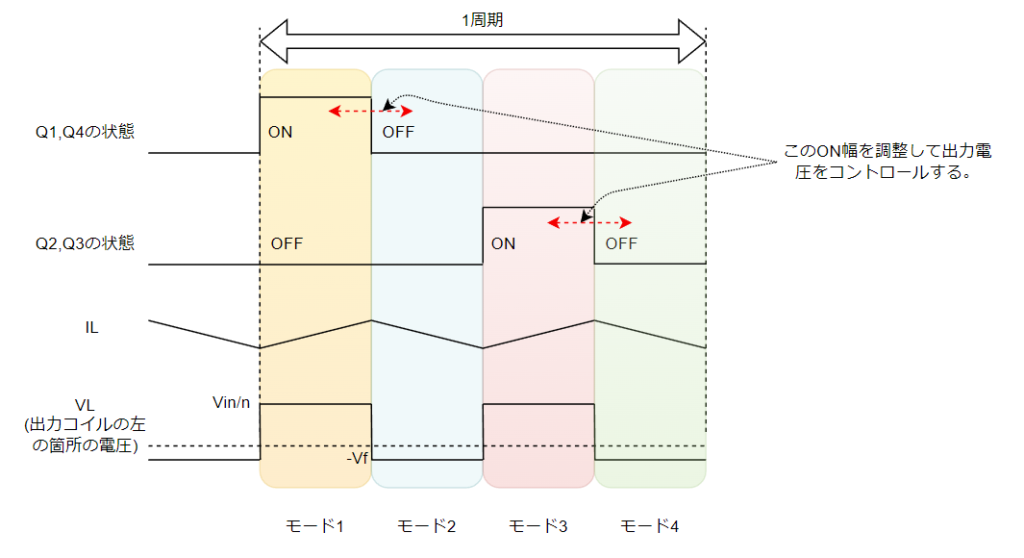
位相シフト制御では全てのスイッチのON幅は固定の50%となります。Q1&Q2を1セット、Q3&Q4を1セットとして、Q3&Q4の位相を遅らせて(シフトさせて)動かします。

(Q1&Q2を進みレグ、Q3&Q4を遅れレグと言います。)
Q1とQ2は絶対に同時にONしません。貫通して大電流が流れてしまうからです。
同様にQ3とQ4は絶対に同時にONしません。
1周期の動作解説
位相シフトフルブリッジコンバータではスイッチのON/OFFの組み合わせで以下の4つのモードに分けることが出来ます。
- モード1:Q1&Q4がON
- モード2:Q2&Q4がON
- モード3:Q2&Q3がON
- モード4:Q1&Q3がON
モード1:Q1&Q4がON

変圧器にはVin電圧がかかり、2次側には変圧比に応じた電圧がコイルにかかります。
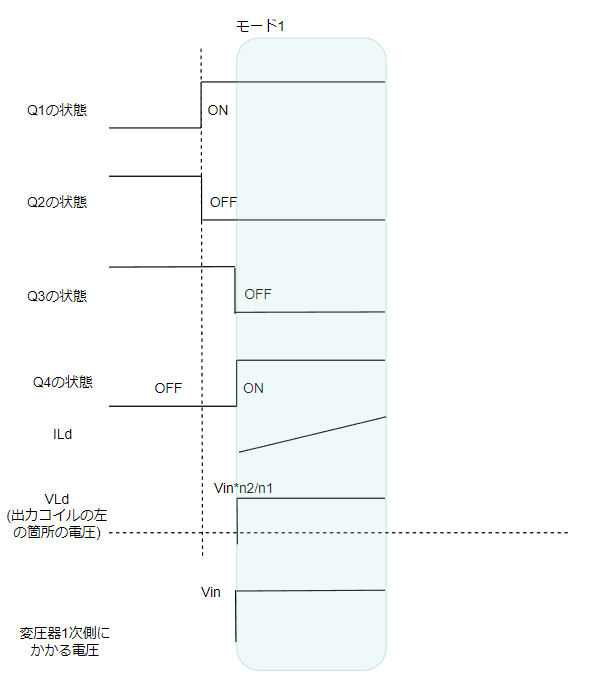
Ldにn2/n1*Vin-Voutがかかりますので、ILdは一定の傾きで増加していきます。
モード2:Q2&Q4がON
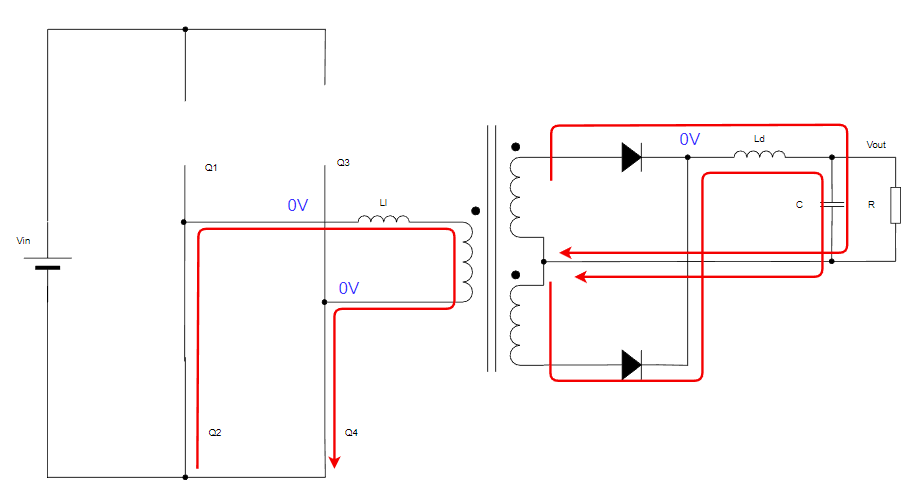
トランスにかかる電圧は0Vとなります。従って2次側の電圧も0Vとなります。
インダクタは電流を流し続けようとするので、環流電流が流れ続けます。
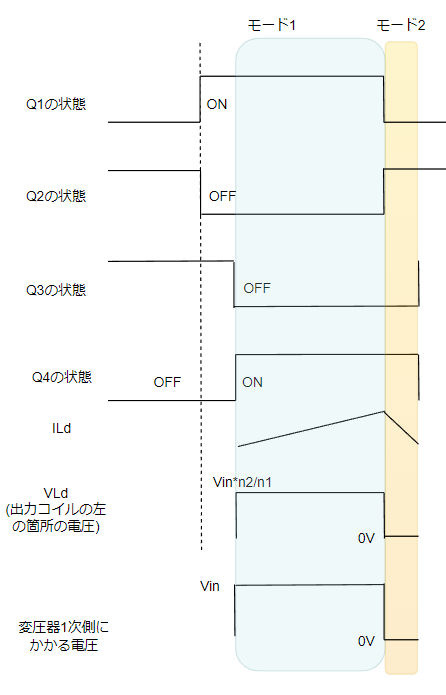
出力コイルには-Voutの電圧がかかり、一定のスピードで電流が落ちていきます。
モード3:Q2&Q3がON
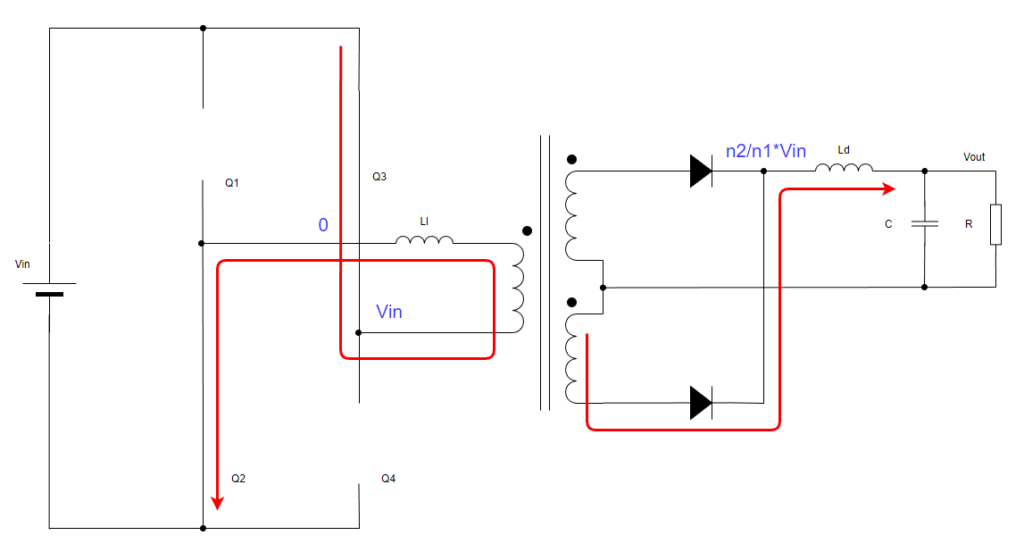
変圧器には-Vin電圧がかかり、2次側には変圧比に応じて±反転した電圧がコイルにかかります。結局モード1と同じ電圧がかかります。
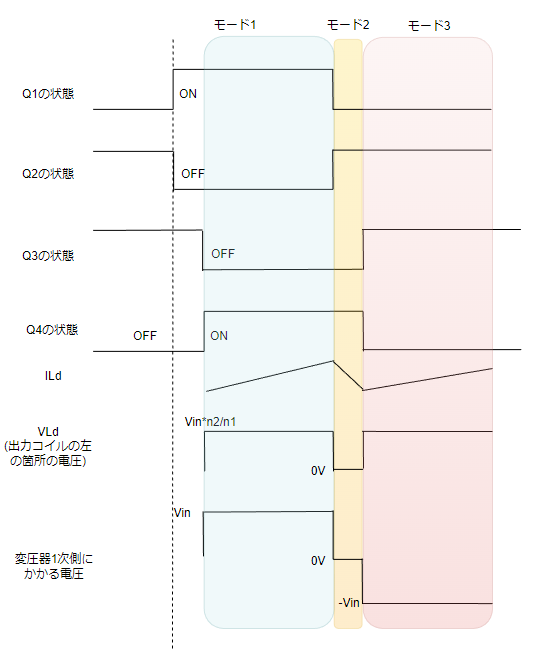
出力コイルにはn2/n1*Vin-Voutの電圧がかかり、一定のスピードで電流が上昇します。
モード4:Q2&Q4がON
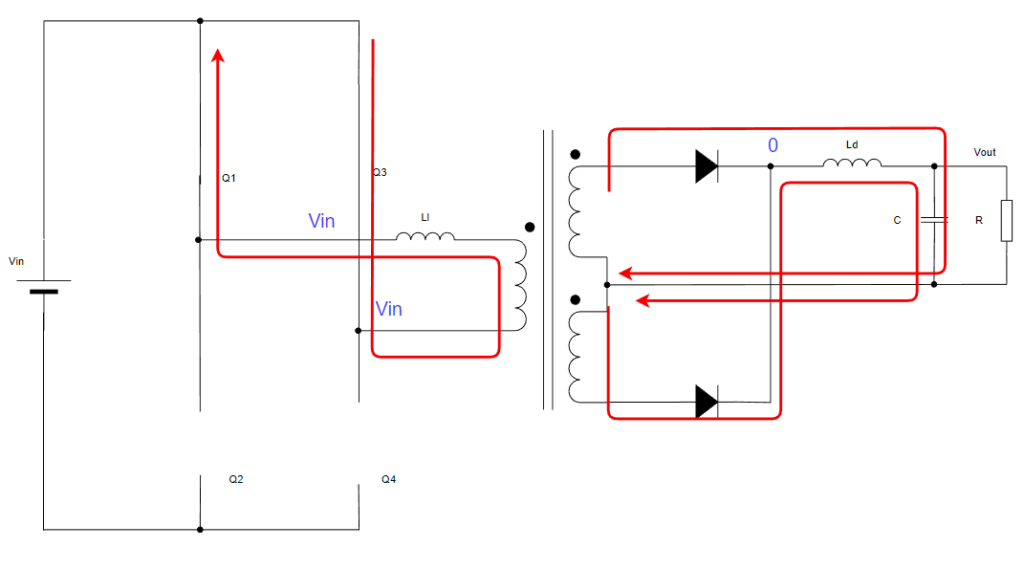
トランスにかかる電圧はVinとVinなので0Vとなります。従って2次側の電圧も0Vとなります。
インダクタは電流を流し続けようとするので、環流電流が流れ続けます。モード2と同様ですね。

出力コイルには-Voutの電圧がかかり、一定のスピードで電流が落ちていきます。
あとは同じことの繰り返しです。
トランス1次側にかかる電圧はVin->0->-Vinと階段状に変化しますが、2次側の出力コイルにはn2/n1*Vinか0Vのどっちかになっており、普通の降圧スイッチングレギュレータのような動きをしています。
2次側のDuty幅を位相シフト量に変換してやって、スイッチをON/OFFさせてやったら、欲しい出力電圧が得られます。
以下では出力電圧の式を導出してみます。
出力電圧の計算式の導出方法
最初に書いた出力電圧の計算式はどうやって導出されるのかを説明します。導出にあたって大事な考え方があります。
それは
一周期のスイッチON/OFF時のコイル電流の増減は足し合わせると0になる。
です。
位相シフトフルブリッジコンバータではT1=T3,T2=T4なのでモード1と2を考えれば3,4も同じことが言えます。なのでモード1,2の組み合わせだけを考えれば大丈夫です。
モード1のコイル電流
コイルには(n2/n1*Vin-Vout)の電圧がかかっています。高校物理で学んだコイルの式を思い出して立式します。
$$\small{V_L=L\frac{Δi_L}{Δt}}$$
$$\small{Δi_L=\frac{V_L}{L}Δt}$$
そのまま値を代入します。
$$\small{
ΔiL_{mode1}=\frac{\frac{n_2}{n_1}V_{in}-V_{out}}{L_d}T_1
}$$
これがモード1のコイル電流の増加分です。
モード2のコイル電流
コイルには-Voutの電圧がかかっています。同じようにコイルの式に値を代入します。
$$\small{
ΔiL_{mode2}=\frac{-V_{out}}{L_d}T_2
}$$
モード1と2のコイル電流の増分を足すと0になる
$$\small{
ΔiL_{mode1}+ΔiL_{mode2}=0\\
\frac{\frac{n_2}{n_1}V_{in}-V_{out}}{L_d}T_1+\frac{-V_{out}}{L_d}T_2=0
}$$
Ldを消します。
$$\small{
\frac{n_2}{n_1}V_{in}-V_{out}T_1-V_{out}T_2=0
}$$
Vout項を移項します。
$$\small{
V_{out}T_1+V_{out}T_2=\frac{n_2}{n_1}V_{in}T_1
}$$
Vout=の形にします。
$$\small{
V_{out}=\frac{n_2}{n_1}V_{in}\frac{T_1}{T_1+T_2}
}$$
T1/(T1+T2)=αとすると
$$\small{
V_{out}=\frac{n_2}{n_1}V_{in}α
}$$
はい。これで終わりですね。PWM制御をやってた人からしたら「なんだ結局、Dutyを位相シフト量に変換しているだけじゃん。」ってなると思います。
はい、本記事はこれで以上です。
誰かの参考になれば幸いです。最後までお読みいただきありがとうございました!