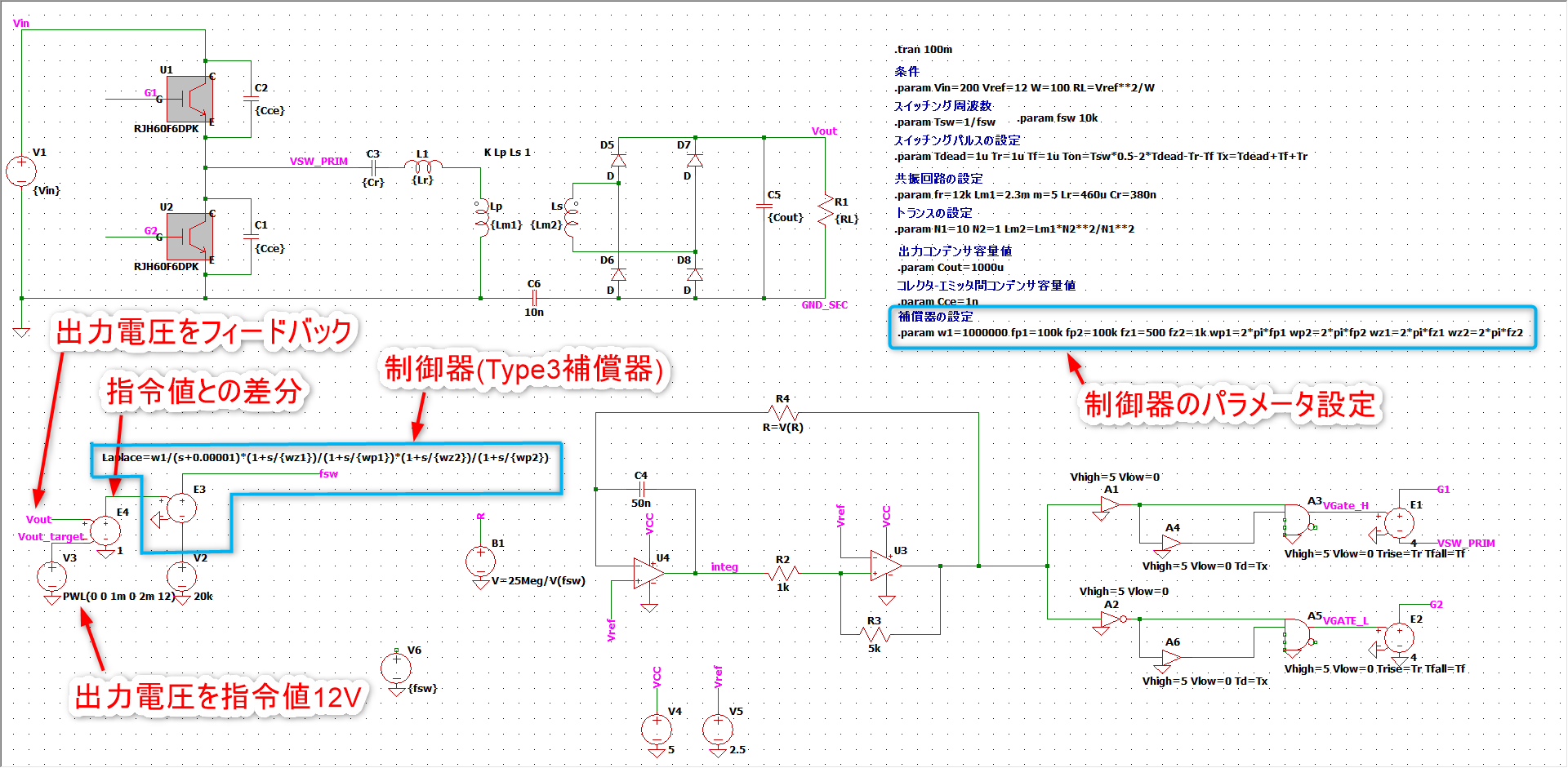
皆様、お疲れ様です。LLCコンバータを勉強する記事の7回目です。今回はLLCコンバータの制御系を設計してみようと思います。
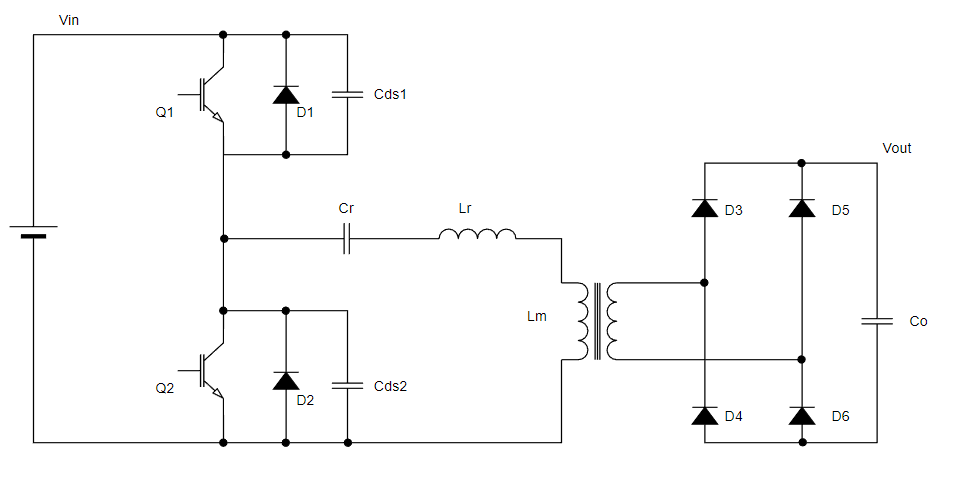
とりあえずLLCコンバータにゲート信号を入れて動かしてみるのはまぁ誰でもできます。でも実際にやりたいのはLLCを動したいってことですよね。
じゃあ、フィードバック制御しないと。でもどうすりゃいいの?という記事です。
1回目:【電源回路】LLCコンバータの動作原理
2回目:【電源回路】LLCコンバータはなぜソフトスイッチングするのか?
3回目:【電源回路】LLCコンバータの出力電圧を計算するpythonスクリプト
4回目:【電源回路】LLCコンバータの設計手順①(パワーラインの設計編)
5回目:【電源回路】LLCコンバータを周波数可変に修正する
6回目:【電源回路】LLCコンバータの周波数特性を調べる
7回目:【電源回路】LLCコンバータの設計手順②(制御設計編)(本記事)
8回目:【LLCコンバータ】インターリーブ運転のリップル低減効果を確認する
9回目:【LLCコンバータ】出力電圧Gvf(s)の周波数特性の負荷依存性を調べる
10回目:【LLCコンバータ】マルチレベル方式LLCコンバータの動作原理
11回目:【LLCコンバータ】LLCコンバータの双方向動作について
12回目:【双方向LLCコンバータ】双方向で電圧調整可能なCLLCコンバータについて解説
13回目:【CLLCコンバータ】LLCとCLLCでは、なぜ出力電圧VSスイッチング周波数の特性が違うのか?
4回目でこの要件を満たすようにパワーラインを設計しました。
| パラメータ | 値 |
|---|---|
| 入力電圧 | 200V |
| 出力電圧 | 12V |
| 共振周波数 | 12kHz |
| 最大負荷電力 | 100W |
パワーラインの定数は以下の通りに設定しました。
| パラメータ | 値 |
|---|---|
| 共振コンデンサ容量値Cr | 380[nF] |
| 漏れインダクタンスLr | 460[uH] |
| 励磁インダクタンスLm | 2.3[mH] |
| 巻き線比(N1/N2) | 10 |
そしてLTspiceで回路を作りました。
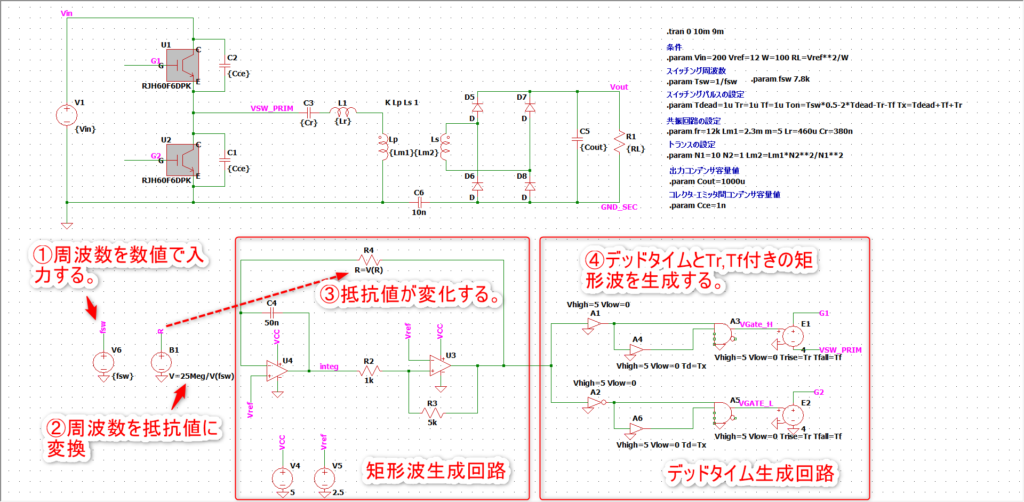
これをフィードバック制御を加えて自動で動作周波数を調整してくれるようにします。
では、始めます。
制御対象の周波数特性を計算する
シミュレーターを使ってLLCコンバータの周波数特性を計算します。今回はPSIMの無料版を使いました。
インストール手順はこちらの記事を参照ください。
こんな感じでLLCコンバータの回路図を用意して↓。
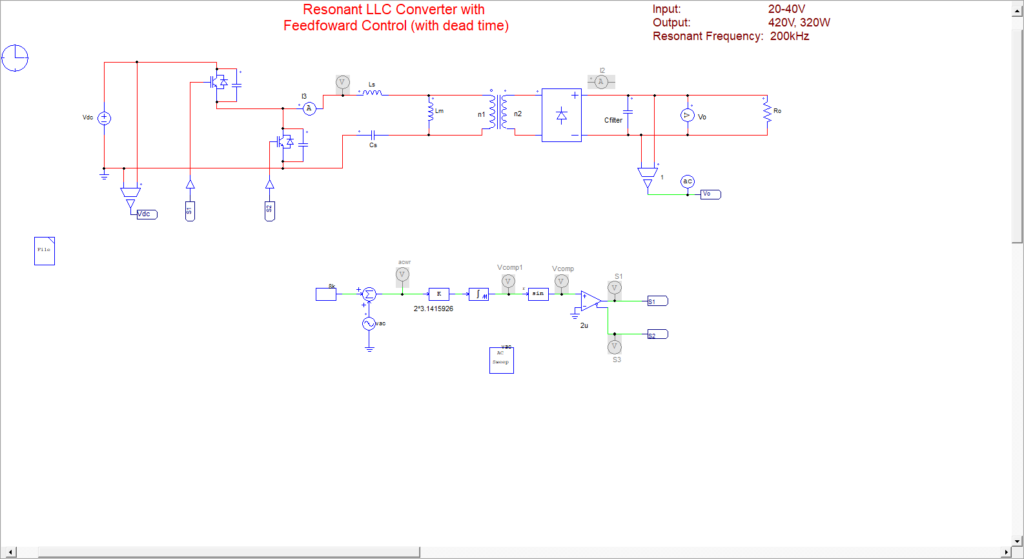
入力周波数値を周波数sweepして出力電圧をモニターすると以下の周波数特性が得られます↓。
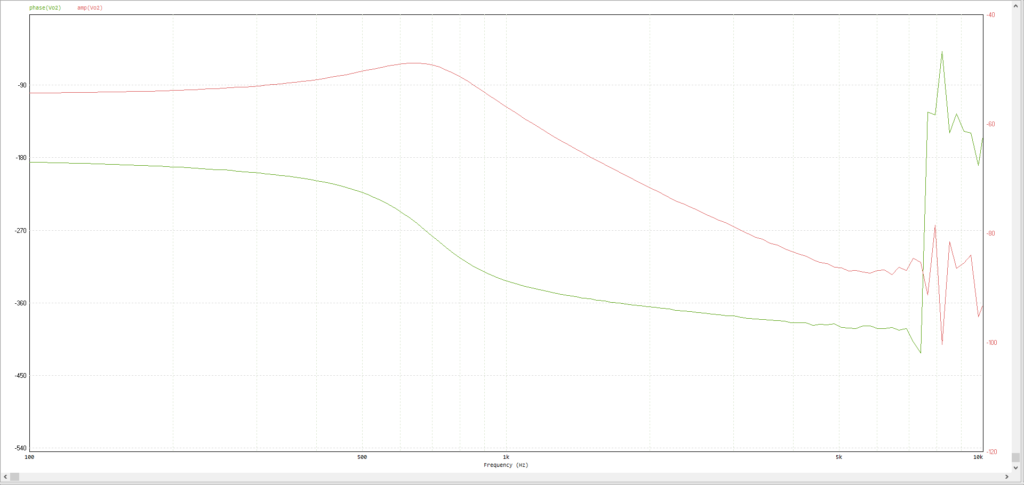
詳細の手順は前回記事で解説しましたので、そちらを参照してください。
これで制御対象の特性がわかりました。
次にコントローラーを設計する前の準備です。
周波数特性を数式にする
先ほどのボード線図を数式にしたいと思います。
ボード線図を良く見るとDCゲイン-55dBくらいで700Hzに折れ点周波数がある2次極だと分かります。
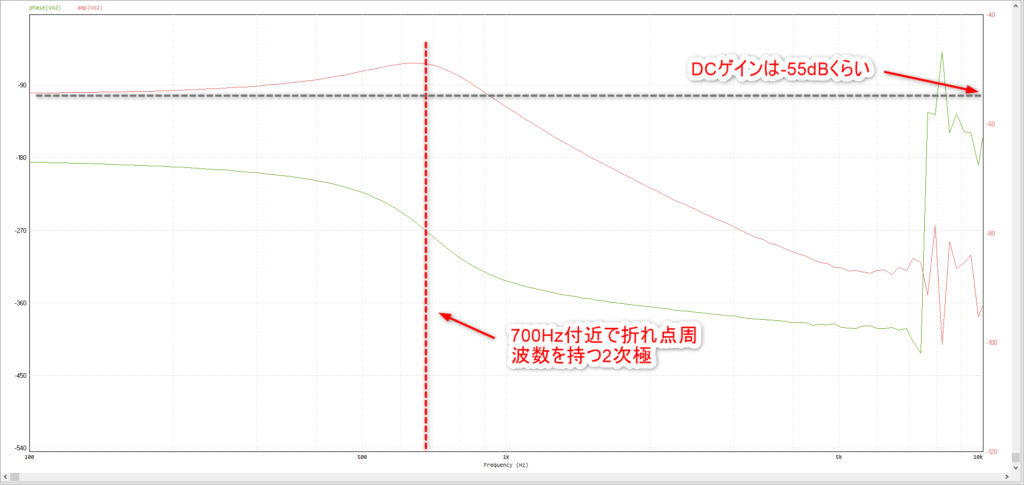
2次極の伝達関数の基本式は以下の通りです。
$$\small{
G(s)=\frac{ω_n^2}{s^2+2ζω_ns+ω_n^2}\\
G(s)=\frac{1}{\frac{s^2}{ω_n^2}+2\frac{ζ}{ω_n}s+1}
}$$
折れ点周波数が700Hzなので
$$\small{
ω_n=2\pi700≒4400
}$$
あとはDCゲインが-55dBなので、
$$\small{
20log(DC_{gain})=-55dB\\
log(DC_{gain})=\frac{-55}{20}\\
DC_{gain}=10^{\frac{-55}{20}}=1.778*10^{-3}
}$$
つまりプラント(制御対象)の伝達関数は
$$\small{
G_{plant}(s)=1.778*10^{-3}\frac{1}{\frac{s^2}{4400^2}+2\frac{ζ}{4400}s+1}
}$$
あとはζを適当に決めればいいです。とりあえずζ=0.5でボード線図を計算してみます。
pythonで以下のようにスクリプトを書いて実行したら、、、
import math
import numpy as np
from matplotlib import pyplot as plt
import sympy as sym
import control as ctl
w_n = 4400
DC_gain = 1.778 * 10**(-3)
z = 0.5
G_plant = ctl.tf([DC_gain],[1/(w_n**2), z/w_n, 1])
gain_plant, phase_plant, w = ctl.bode(G_plant, Plot=False)
f = w/2/np.pi
gain_plant_dB = 20*np.log10(gain_plant)
phase_plant_deg = phase_plant * 180/np.pi
fig, ax = plt.subplots(2,1)
ax[0].semilogx(f, gain_plant_dB)
ax[0].set_yticks([-80,-70,-60,-50,-40])
ax[0].grid(which = "both", axis = "x")
ax[0].grid(which = "both", axis = "y")
ax[0].set_ylabel("gain[dB]")
ax[1].semilogx(f, phase_plant_deg)
ax[1].set_yticks([-180,-135,-90,-45,0])
ax[1].grid(which = "both", axis = "x")
ax[1].grid(which = "both", axis = "y")
ax[1].set_ylabel("phase[deg]")
ax[1].set_xlabel("f[Hz]")以下のボード線図が得られました。
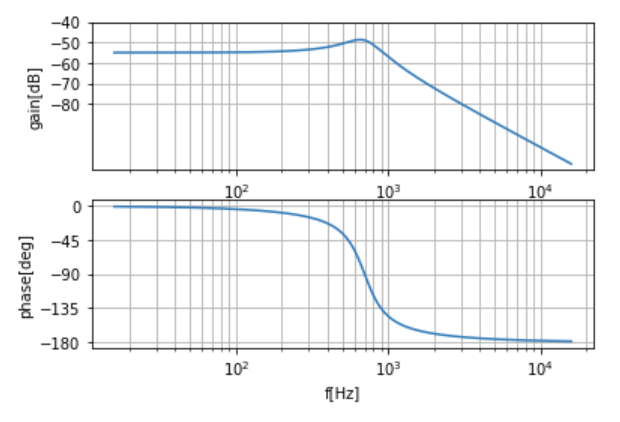
まぁいい感じですかね。本物は高周波領域はガチャガチャっとなります。スイッチングの無駄時間の影響です。
まぁ低域で安定性を確保するって前提で、まぁこれで良いかなと。
とりあえず、これでプラント伝達関数を数式化できました。
コントローラーを加えて安定性を確保する
あとはコントローラーを加えて安定性を確保します。コントローラーはオーソドックスにType3補償器を入れます。
Type3補償器の伝達関数は以下の通りです。
$$\small{
G_c(s)=\frac{ω_1}{s}\frac{\frac{s}{ω_{z1}}+1}{\frac{s}{ω_{p1}}+1}\frac{\frac{s}{ω_{z2}}+1}{\frac{s}{ω_{p2}}+1}
}$$
ω1:DCゲイン
ωz1:ゼロ点その①
ωz2:ゼロ点その②
ωp1:極その①
ωp2:極その②
制御のイメージはプラントの2次極700Hzにゼロ点2つをドンドンっとぶち当てて、キャンセルします。
あとはDCゲインを上げ下げしてだいたい1kHzくらいのゼロクロス周波数を目指すって感じです。
pythonでスクリプトを作って、トライ&エラーを繰り返して以下の設定にしました。
| パラメータ | 値 |
|---|---|
| DCゲイン | 1000000 |
| ポール周波数① | 100[kHz] |
| ポール周波数② | 100[kHz] |
| ゼロ点周波数① | 500[Hz] |
| ゼロ点周波数② | 1[kHz] |
pythonスクリプトは以下の通りです。Gcがコントローラーの伝達関数でGplantと掛け算することで系全体の伝達関数Gtotalを計算しています。
fp1 = 100000
fp2 = 100000
fz1 = 500
fz2 = 1000
w = ctl.tf([1000000],[1,0])
Gc1 = ctl.tf([1/(2*np.pi*fz1), 1],[1/(2*np.pi*fp1), 1])
Gc2 = ctl.tf([1/(2*np.pi*fz2), 1],[1/(2*np.pi*fp2), 1])
Gc = w * Gc1 * Gc2
Gtotal = Gc * G_plant
gain, phase, w = ctl.bode(Gtotal, Plot=False)
f = w/2/np.pi
gain_dB = 20*np.log10(gain)
phase_deg = phase * 180/np.pi
fig, ax = plt.subplots(2,1)
ax[0].semilogx(f, gain_dB)
ax[0].set_yticks([-60,-40,-20,0,20,40,60])
ax[0].grid(which = "both", axis = "x")
ax[0].grid(which = "both", axis = "y")
ax[0].set_ylabel("gain[dB]")
ax[1].semilogx(f, phase_deg)
ax[1].set_yticks([-180,-135,-90,-45,0])
ax[1].grid(which = "both", axis = "x")
ax[1].grid(which = "both", axis = "y")
ax[1].set_ylabel("phase[deg]")
ax[1].set_xlabel("f[Hz]")これで計算したボード線図が以下の通り。
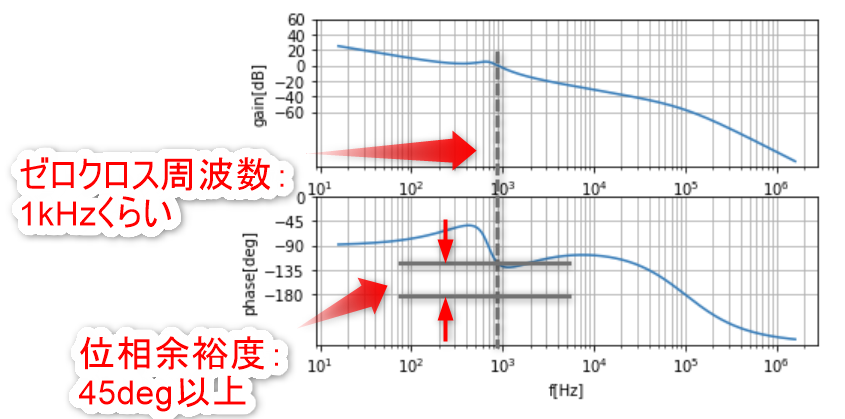
位相余裕度が45deg以上確保できているので、安定です。
安定性って何?という方はこちらの記事で解説しておりますので、良かったら読んでみて下さい。
これで回路動作を見てみます。
回路に反映して動作確認
LTspiceにフィードバックの経路を追加しました。
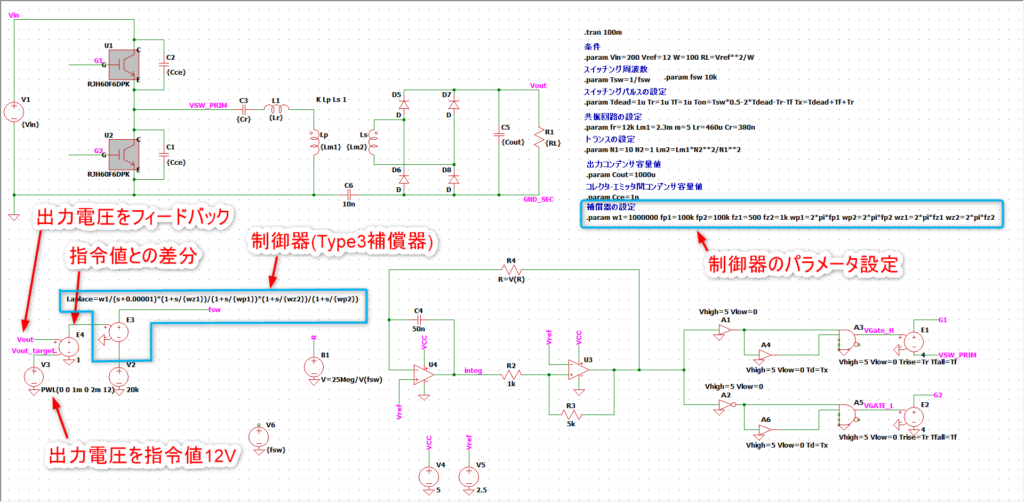
ポイントとしてはV2で初期の動作周波数を設定したことです。
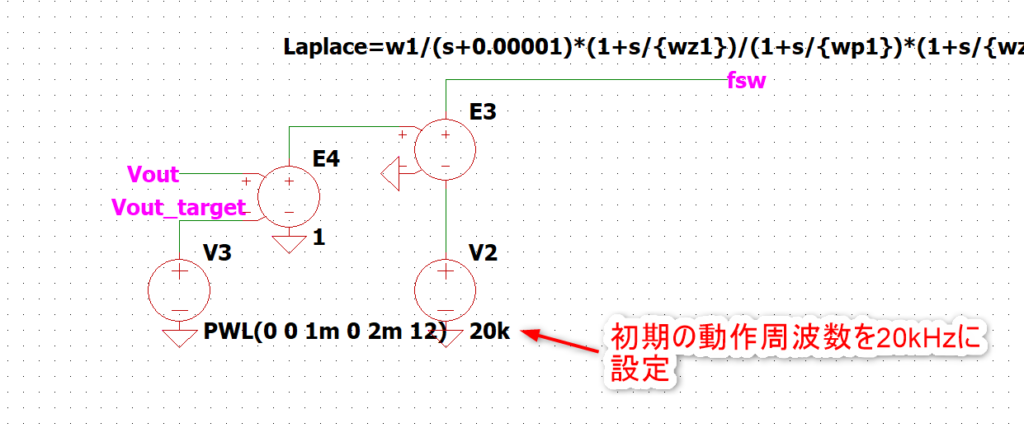
これがないと動作周波数が0HzからスタートしてしまうとLLCが動かなくなります。Vout VS fswを見るとわかりやすいかと思います。
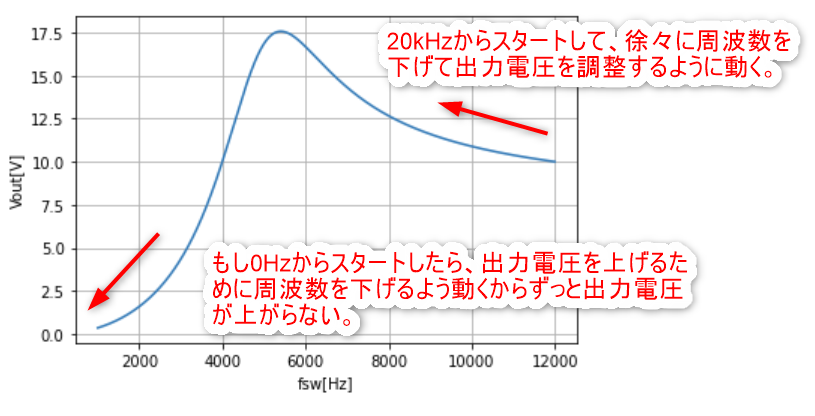
シミュレーション結果は以下の通りです。
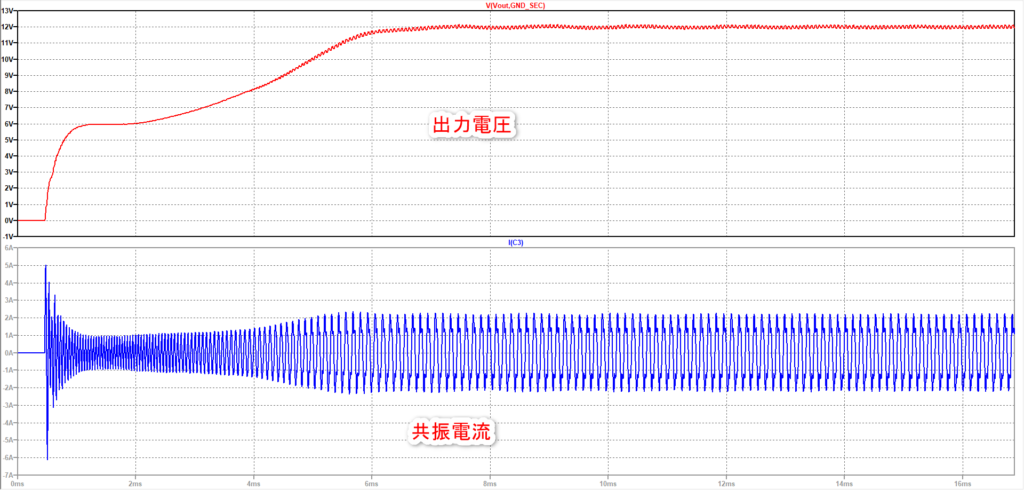
出力電圧がちゃんと狙いの12Vに収束していますね。
ちょっとリップル電圧がデカいかな?そのせいで周波数がちょっと揺れて感じがしますね。
でも、まぁ一旦動いているからいいんじゃないかなと。
はい、本記事は以上で終わります。
誰かの参考になれば幸いです。最後までお読みいただきありがとうございました!!