皆様、お疲れ様です。LLCコンバータを勉強する記事の4回目です。
そろそろ回路を作ってみよう。ということで私のLLCコンバータの回路設計手順を記事にします。
1回目:【電源回路】LLCコンバータの動作原理
2回目:【電源回路】LLCコンバータはなぜソフトスイッチングするのか?
3回目:【電源回路】LLCコンバータの出力電圧を計算するpythonスクリプト
4回目:【電源回路】LLCコンバータの設計手順①(パワーラインの設計編)(本記事)
5回目:【電源回路】LLCコンバータを周波数可変に修正する
6回目:【電源回路】LLCコンバータの周波数特性を調べる
7回目:【電源回路】LLCコンバータの設計手順②(制御設計編)
8回目:【LLCコンバータ】インターリーブ運転のリップル低減効果を確認する
9回目:【LLCコンバータ】出力電圧Gvf(s)の周波数特性の負荷依存性を調べる
10回目:【LLCコンバータ】マルチレベル方式LLCコンバータの動作原理
11回目:【LLCコンバータ】LLCコンバータの双方向動作について
12回目:【双方向LLCコンバータ】双方向で電圧調整可能なCLLCコンバータについて解説
13回目:【CLLCコンバータ】LLCとCLLCでは、なぜ出力電圧VSスイッチング周波数の特性が違うのか?
参考資料はここです。天下のTI様の資料です。
まず設計手順を一通り説明した後、実践してみようと思います。
LLCコンバータの設計方法がよくわからない。とお悩みの方の参考になれば幸いです。
では始めます。
巻き線比をざっくり設定する
まず巻き線比です。入力電圧と狙いの出力電圧から以下の式を使ってざっくり決めます。
$$\small{
V_{out}=\frac{1}{2}V_{in}×\frac{N_2}{N_1}
}$$
Vout:出力電圧[V]
Vin:入力電圧[V]
N1:1次側巻き線数
N2:2次側巻き線数
この式はLLCコンバータの共振周波数frでスイッチング動作させたときに成立する式です。
巻き線比を設定するときのポイントは
- Voutが所望の出力電圧値より少し低い電圧で計算する。
例えば、Vout=12Vが欲しいとかなら、10Vがfrで出るように設定するって感じです。
なぜそうするかというとスイッチング周波数はfm~frの間で動かしたいので、出力電圧狙い値はfm~frの間になる様にしよう。って考えです。
S=5,Q=0.5として出力電圧の特性カーブを描く
非対称ハーフブリッジ型LLCコンバータの出力電圧は以下の式で決まります。
$$\small{
V_{out}=\frac{1}{2}V_{in}\frac{1}{\sqrt{\left(1+\frac{1}{S}-\frac{1}{SF^2}\right)^2+Q^2\left(F-\frac{1}{F}\right)^2}}
\\
S=\frac{L_m}{L_r},F=\frac{f}{f_r},f_r=\frac{1}{2\pi\sqrt{L_rC_r}},Q=\frac{\sqrt{\frac{L_r}{C_r}}}{R_L’},R_L’=\frac{8}{\pi^2}\left(\frac{N_1}{N_2}\right)^2R_L
}$$
Vout:出力電圧[V], Vin:入力電圧[V], Lm:励磁インダクタンス[H], Lr:漏れインダクタンス[H],Cr:共振コンデンサ[F], f:スイッチング周波数[Hz], fr:Lr&Cr共振周波数[Hz], N1:1次巻き線, N2:2次巻き線, RL:負荷抵抗[Ω]
最初はまずS=5、Q=0.5に固定して計算します。(大体この辺りが相場値のようです。)
S=5,Q=0.5に固定することでCr,Lr,Lmが以下の式で計算できます。
$$\small{
C_r=\frac{1}{2\pi f_rR_L’Q}
}$$
$$\small{
L_r=\frac{1}{(2\pi f_r)^2C_r}
}$$
$$\small{
L_m=L_r*S
}$$
これで計算したCr,Lr,Lmと前項で決めたN1,N2とS,Qを先ほどの出力電圧の計算式に代入してfを振って出力電圧の曲線を描きます。
これで所望の出力電圧が得られるかを確認します。
要件を満たせなかったからQを下げる
もし出力電圧の狙い値が得られなかったら、Q値を下げて再度出力電圧曲線を描きます。
これは励磁インダクタンスを下げて、出力電圧カーブのピーク値を尖らせているイメージです。
なぜSをいじらないのか?
もしSを大きくすると励磁インダクタンスは大きくなる方向なので、より出力電圧の狙い値が得られない方向になります。
もしSを小さくするとfrの共振周波数とfmの共振周波数(=出力電圧のピーク周波数)の間が狭くなります。
これも以下の理由から具合があんまりよくないです。
- 操作する周波数範囲が狭くなる。->発振しやすくなる。
- fmに近づくと上記の出力電圧の式が適用できなくなってくる。->出力電圧狙い値が計算できない。
なので、ちょっとずつQを下げて出力電圧が満たすようなQ値を選択して、共振回路の定数を決定します。
デッドタイムの目安を確認しておく
上下のスイッチの切り替え時の待ち時間(=デッドタイム)の最小値を以下の式で計算して、大体デッドタイムの目安を確認しておきます。
$$\small{
T_{dead}≧16C_{eq}f_{sw}L_m
}$$
Ceq:スイッチの寄生容量
ざっくりで良いです。ここの値を絶対に割らないようにデッドタイムを設定します。
回路で動きを確認する
ここまで来たら回路シミュレータで回路を作成してシミュレーションで以下の動きを見ます。
- 出力電圧波形
- 出力電流波形
- 共振電流波形
- スイッチ電流
- スイッチ両端電圧
これらを見ておかしい動きがないかを確認します。
おかしかったらちょっとずつ修正します。
はい、以上です。では実践でLLCコンバータを設計してみます。
実践編:LLCコンバータを設計してみる
上記を書いただけでは「は?ほんとに出来るの?」って話なので試しに以下の要件で作ってみます。
| パラメータ | 値 |
|---|---|
| 入力電圧 | 200V |
| 出力電圧 | 12V |
| 共振周波数 | 12kHz |
| 最大負荷電力 | 100W |
巻き線比をキリの良い値に設定する
200V->12VなのでざっくりN1:N2=10:1にしておけば12Vは得られそうです。
共振点12kHzでの出力電圧は
$$\small{
V_{out}(fsw=12kHz)=\frac{1}{2}V_{in}\frac{N_2}{N_1}\\
V_{out}(fsw=12kHz)=\frac{1}{2}200\frac{1}{10}=10V
}$$
10Vです。スイッチング周波数を共振周波数の少し前の10kHz付近で動かして12Vを得たいなぁというイメージです。
というわけで巻き線比は10:1とします。
| パラメータ | 値 |
|---|---|
| 巻き線比(N1/N2) | 10 |
m=5,Q=0.5として出力電圧の特性カーブを描く
先にRL’を計算しておきます。
$$\small{
R_L’=\frac{8N^2}{\pi^2}R_L=\frac{8N^2}{\pi^2}\frac{V_{out}^2}{P_{out}}\\
R_L’=\frac{8*10^2}{\pi^2}\frac{12^2}{100}=116.7[Ω]
}$$
以下の式を使ってCr->Lr->Lmの順番に計算します。
$$\small{
C_r=\frac{1}{2\pi f_rR_L’Q}=\frac{1}{2\pi 12*10^3*116.7*0.5}≒220[nF]
}$$
$$\small{
L_r=\frac{1}{(2\pi f_r)^2C_r}=\frac{1}{(2\pi 12*10^3)^2 220n}≒800[uH]
}$$
$$\small{
L_m=L_r*m=800*5=4[mH]
}$$
ひとまず共振回路の定数は以下です。
| パラメータ | 値 |
|---|---|
| 共振コンデンサ容量値Cr | 220[nF] |
| 漏れインダクタンスLr | 800[uH] |
| 励磁インダクタンスLm | 4[mH] |
この条件での出力電圧特性は以下のようになります。

出力電圧12Vを出力できていないのでダメですね。
要件を満たせなかったからQを下げる
Qを0.1下げてみます。
さきほどと同じ計算をして、Cr,Lr,Lmは以下のようになりました。
| パラメータ | 値 |
|---|---|
| 共振コンデンサ容量値Cr | 280[nF] |
| 漏れインダクタンスLr | 600[uH] |
| 励磁インダクタンスLm | 3[mH] |
この条件での出力電圧特性は以下のようになります。
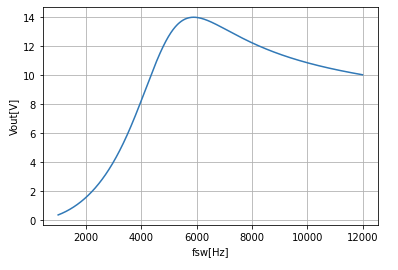
良い感じです。
ただ12Vがだいぶ低域の共振周波数に近いです。実際は回路内の電圧降下の影響を受けると考えると12Vを得られる周波数はもう少し低域になることが予想されます。
また、正弦波近似の波形は低域になる程ずれてくるので、もう少し狙い値を高域に持っていきたいです。
なのでさらにQを0.1下げて、Q=0.3で再計算します。
また同じ計算をして、Cr,Lr,Lmは以下のようになりました。
| パラメータ | 値 |
|---|---|
| 共振コンデンサ容量値Cr | 380[nF] |
| 漏れインダクタンスLr | 460[uH] |
| 励磁インダクタンスLm | 2.3[mH] |
この条件での出力電圧特性は以下のようになります。
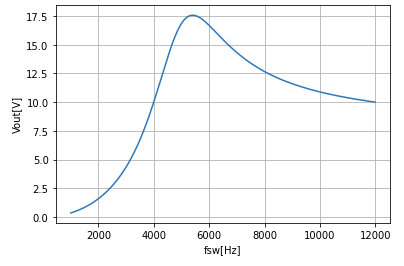
いい感じですね。定数設定はこれにします。
デッドタイムの目安を確認しとく
デッドタイムの下限値は以下の式で計算できます。
$$\small{
T_{dead}≧16C_{eq}f_{sw}L_m
}$$
Ceqはスイッチの寄生容量
使用する素子によると思いますが、今回はIGBT(RJH60F6DPK)を想定します。データシートを見ると

Coesが150pF、Cresが65pFです。
こちらの資料によるとコレクタ-エミッタ間容量はCoes-Cresで求められます。まぁざっくり100pFとします。
$$\small{
T_{dead}≧16*100p*10k*2.3m=36.8[nsec]
}$$
だいたい40nsec以上にしておけば良さそうですね。10kHzだと1周期が100usecなので1%以下ですね。適当に設定しておけば余裕です。
回路で動きを確認する
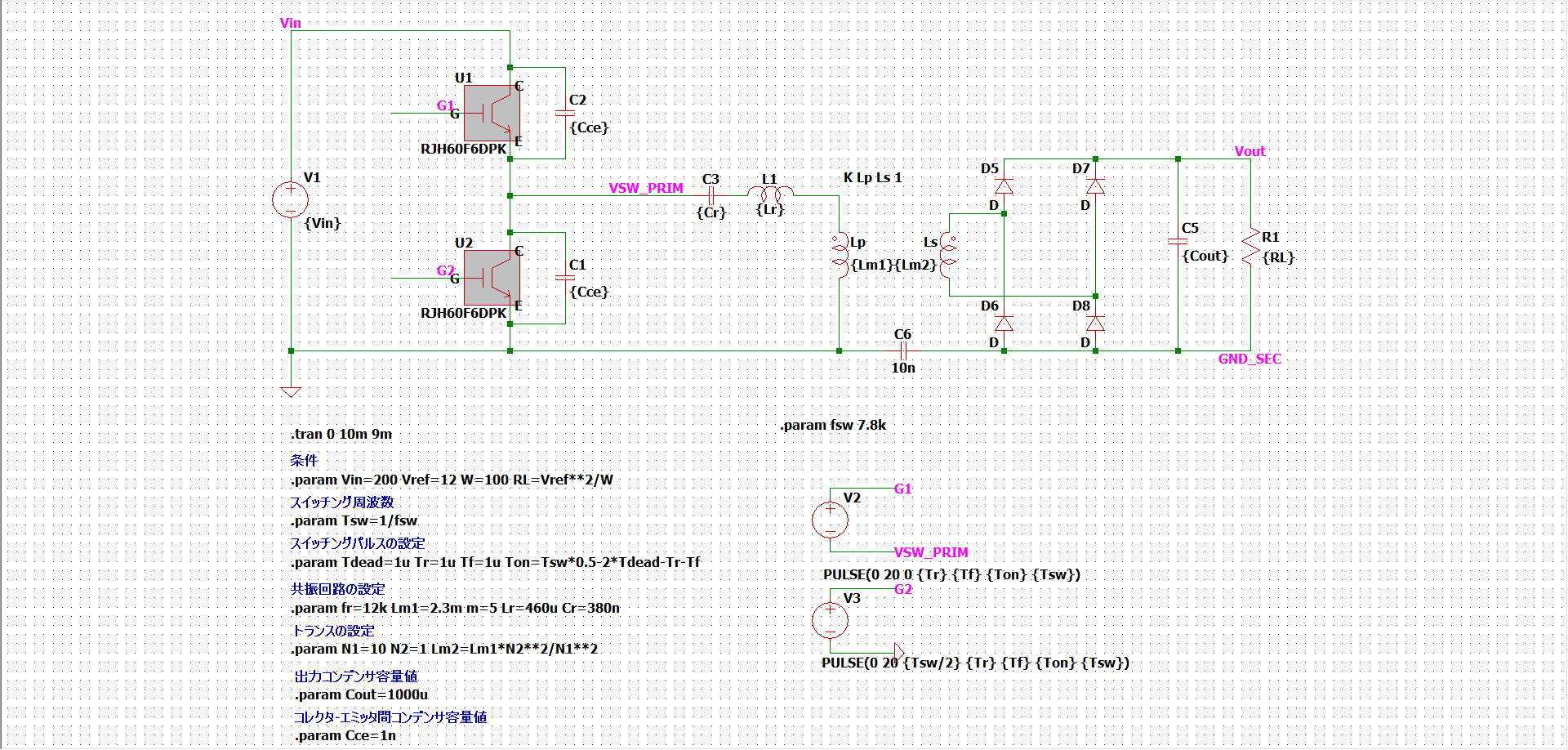
とりあえず回路を作ってみました。
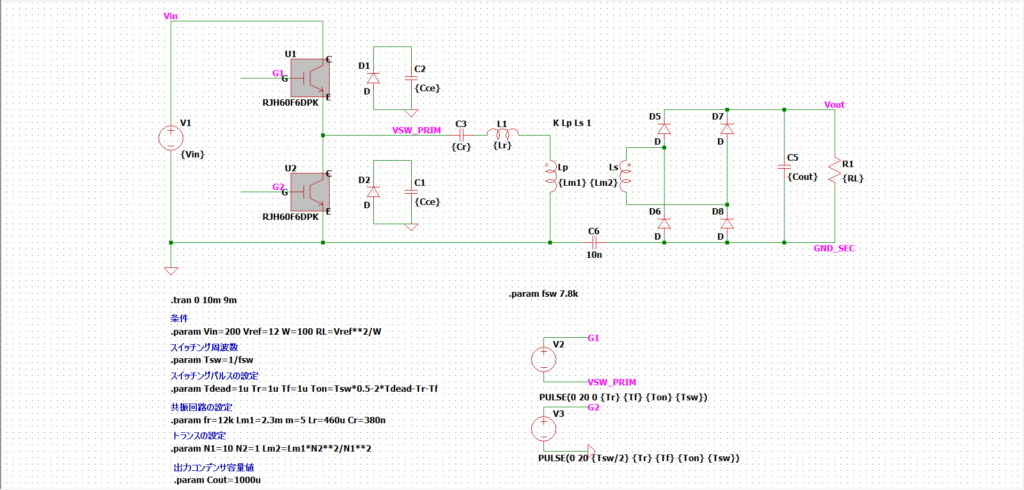
ちなみにRJH60F6DPKのspice modelはこちらです。
波形は以下です。
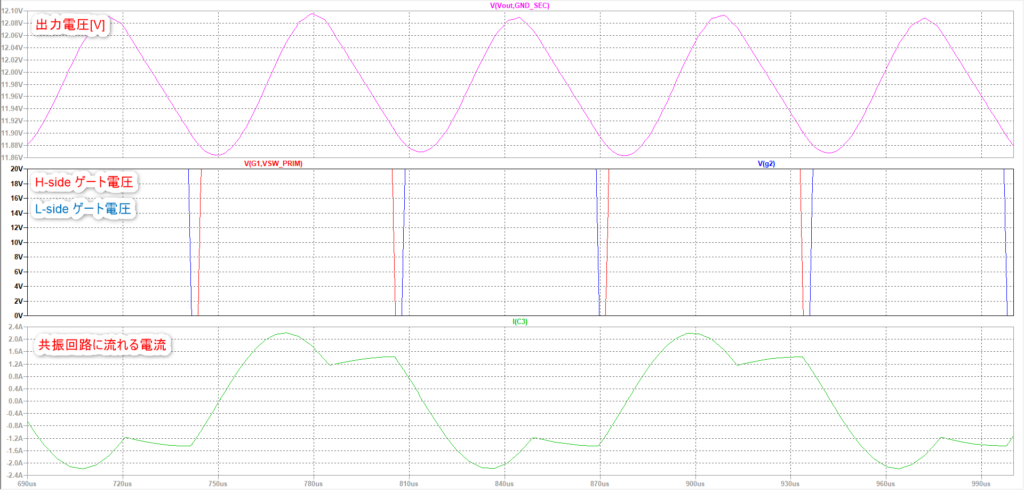
ちゃんと動いてそうですね。
想定では10kHz付近で12V出力でしたが、7.8kHz付近で12Vが出力しています。ダイオードのドロップなどの影響と考えられます。
ZVSしているのか?
詳細はこちらの記事で解説していますが、LLCコンバータはターンオフ時に励磁電流が寄生コンデンサに転流することで実現します。
ためしにH-sideターンオフ時のコレクタ-エミッタ間電圧とコレクタ電流をモニターしてみます。
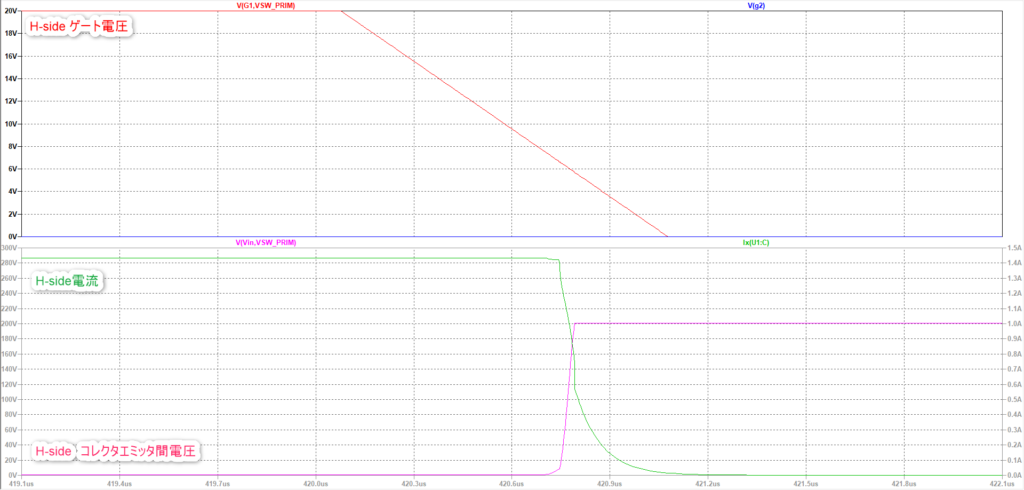
ってか転流しているかどうかは見れませんね。なぜならIGBTのサブサーキット内に寄生コンデンサが含まれているから。
どうやってZVSしているかを判断したら良いんでしょうかね。。。?
L-sideの電流をモニターして電流が流れていたら、L-sideの寄生コンデンサに転流していると判断できるよね。という発想でL-sideの電流をモニターしてました↓。
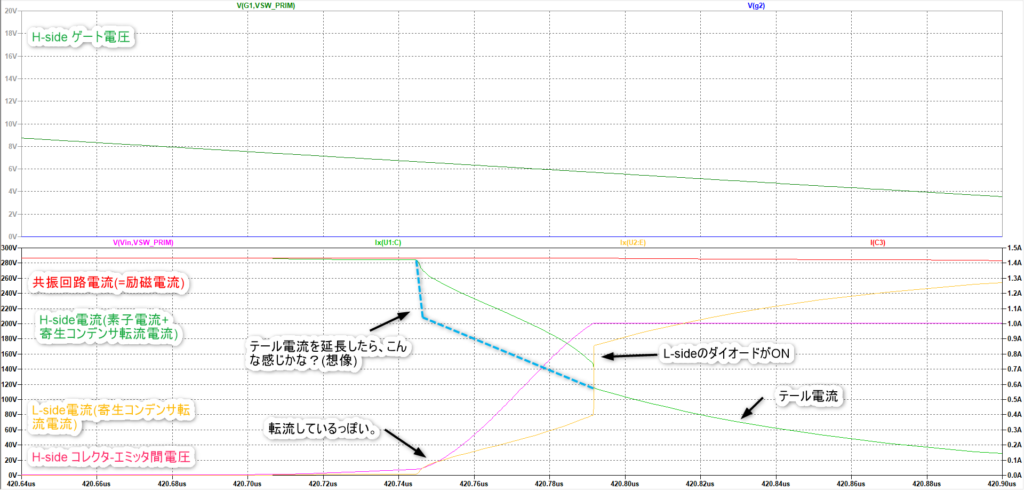
ゲート電圧が8Vを切ったくらいから徐々にL-side電流が増加しています。H-sideがOFFして電流が転流していると考えられます。
しかしテール電流が長くてその間に電圧が上昇してしまっていますね。
これだと損失がデカそうです。
ソフトスイッチングするためにテール電流が減少するまでH-sideコレクタ-エミッタ間電圧が上昇しづらいようにしてやります。
具体的には各スイッチのコレクタ-エミッタ間電圧にコンデンサを追加してやりました。
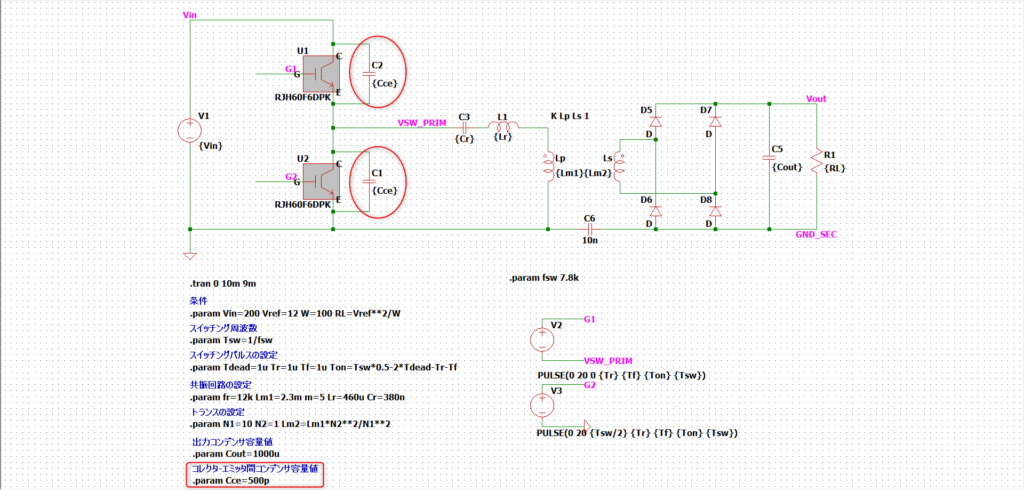
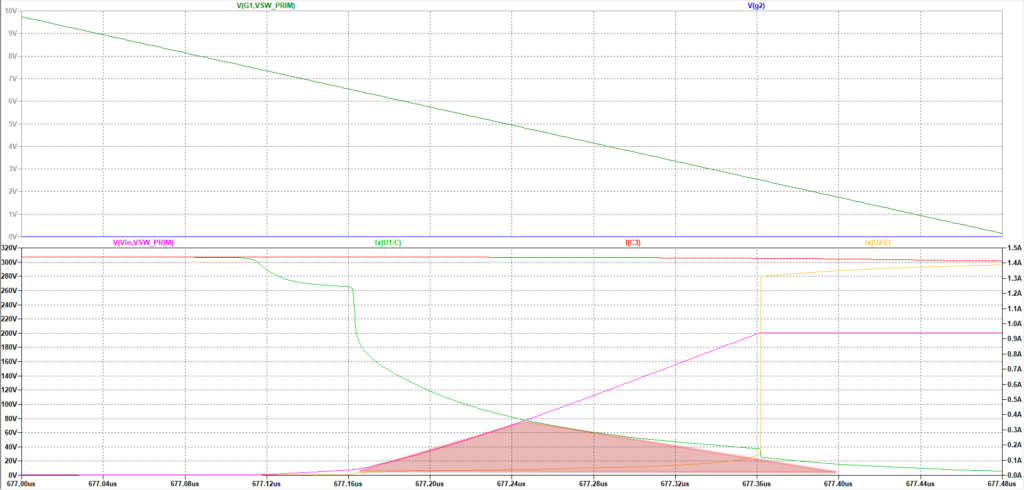
損失領域を赤で色付け
いい感じですね。さらにコンデンサを大きくしてみます。
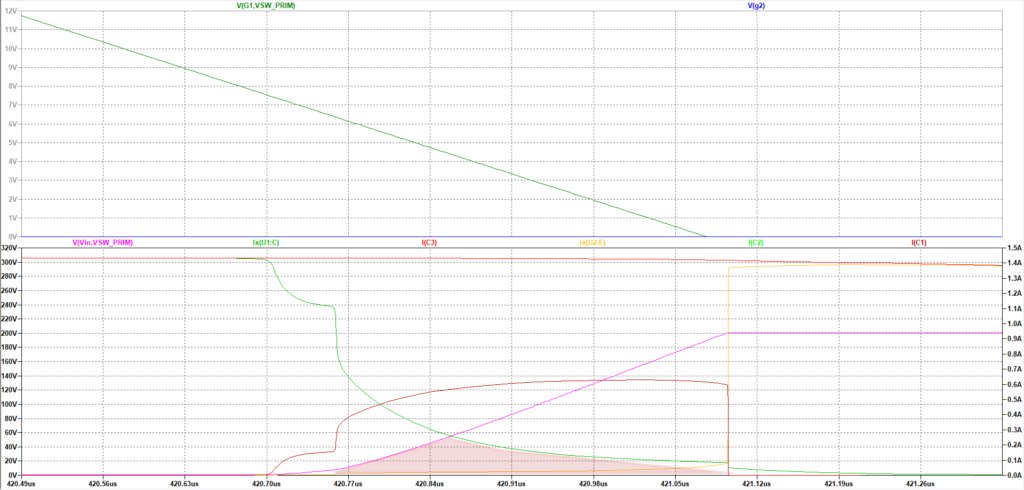
損失領域を赤で色付け
コレクタ-エミッタ間電圧の遷移を遅らせるようにしたらZVSしやすくなるって感じですね。
まぁこんなもんかな?って感じで本記事は終わります。
次回は電圧を一定制御するようにフィードバック制御を設計してみようと思います。
誰かの参考になれば幸いです。最後までお読みいただきありがとうございました!!