皆様、お疲れ様です。本日はRC回路の伝達関数の求め方を記事にまとめてみようと思います。
こんなのですね↓。
・RC回路の伝達関数の求め方がわからない!
・そもそも何で伝達関数を求めないといけないのか?
・伝達関数を求めてどうなる?
とお悩みの方の参考になれば幸いです。ではやってみましょう。
結論:RC回路の伝達関数はこれ。
$$G(s)=\frac{VOUT(s)}{VIN(s)}=\frac{1}{sRC+1}$$
求め方の手順は以下の通りです。
①時間領域tでのvout(t)=~の式を立てる。
②その式を周波数領域に持っていく(ラプラス変換)
③その式をVOUT(s)/VIN(s)の形にする。
初めてだとわからないもんです。実際にやってみましょう。
何で我々は伝達関数を求めるのか?
まずモチベーションの確認です。求め方を知るより重要です。たぶん。
なぜ伝達関数を求めたいんでしょうか?皆さん、一度考えてみて下さい。

大学の課題

勉強会で宿題
というような、まぁわかりますが、、、求めてないです。まぁもったいぶることでもないので、答えを言うと、
・時間tのときの出力値を知りたい!
・時間領域tで計算するとややこしいけど、周波数領域sで計算するとめちゃ簡単に求められる!
未来がどうなるかを予測したい!!!が大きなモチベーションでもっと楽に計算したい!!!と編み出されたのが「時間領域tを周波数領域sに持って行って計算する。」という手法です。
その周波数領域sで計算された入出力関係式を伝達関数と呼んでいるということですね。
RC回路伝達関数の求め方
時間領域で出力=の式を立てる
最初に時間tにおけるvoutはどうなるのかを計算式で表してみましょう。これがね。まぁむずい。最大の関門です。
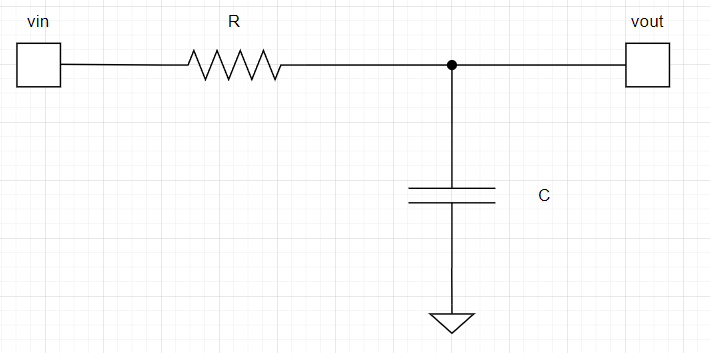
まず、vout(t)というのはコンデンサ電圧vc(t)と同じ電圧になりますね。
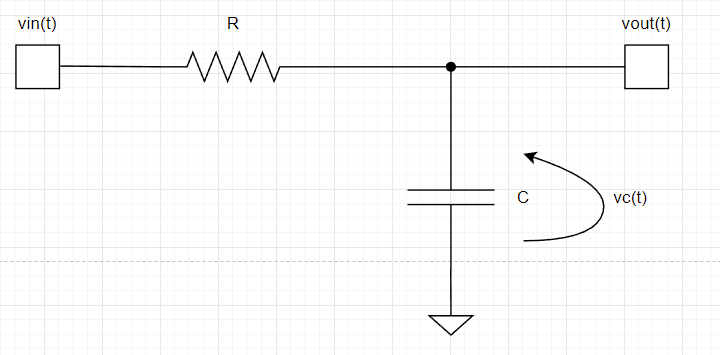
$$v_{out}(t)=v_c(t)$$
ここで高校物理を思い出しましょう。コンデンサの式です。そうQ=CVですね。
$$q(t)=C*v_c(t)$$
$$v_c(t)=\frac{q(t)}{C}$$
q(t)というのは電荷のことでコンデンサに流れる電流ic(t)の積分です。
$$q(t)=\int_0^{t}i_c(t)dt$$
この式をvcの式に入れます。
$$v_c(t)=\frac{1}{C} \int_0^{t}i_c(t)dt$$
vout(t)=vc(t)なので、
$$v_{out}(t)=\frac{1}{C} \int_0^{t}i_c(t)dt$$
これでOKです。
じゃあ次は電流ic(t)はどうなるか?を考えます。下図の通り、コンデンサに流れる電流は抵抗に流れる電流と同じです。
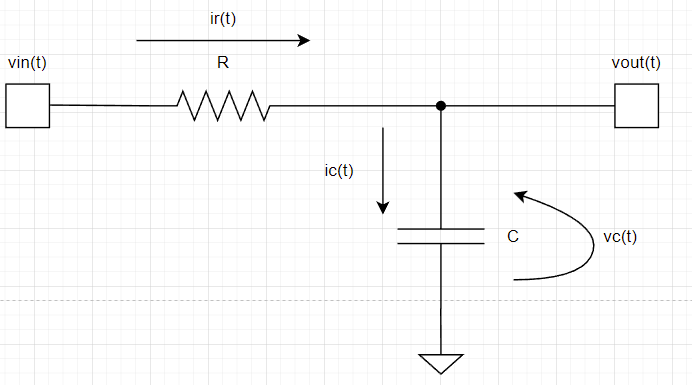
$$i_c(t)=i_r(t)$$
じゃあ、抵抗に流れる電流はなんぼ?と考えると単純にオームの法則です。
$$i_c(t)=i_r(t)=\frac{v_{in}(t)-v_{out}(t)}{R}$$
はい。これを先ほどの青枠で囲んだ式に追加しておきましょう。
$$v_{out}(t)=\frac{1}{C} \int_0^{t}i_c(t)dt$$
$$i_c(t)=\frac{v_{in}(t)-v_{out}(t)}{R}$$
これで今日の計算の8割は終わりです。
時間領域から周波数領域に持っていく(ラプラス変換)
時間領域から周波数領域に持っていく行為をラプラス変換と言います。ラプラス変換表を見ながら、先ほどの式を変換しましょう。
$$\begin{cases}
V_{OUT}(s)=\frac{1}{sC}I_C(s) \\
I_C(s)=\frac{V_{IN}(s)-V_{OUT}(s)}{R} \\
\end{cases}$$
ICを消してVOUT(s)/VIN(s)=~の形に持っていく
あとは単純計算あるのみです。上の式にICを代入します。
$$ V_{OUT}(s)=\frac{1}{sC}* \frac{V_{IN}(s)-V_{OUT}(s)}{R} $$
$$ V_{OUT}(s)=\frac{1}{sRC}VIN(s)- \frac{1}{sRC}VOUT(s)$$
$$(1+\frac{1}{sRC})V_{OUT}(s)=\frac{1}{sRC}VIN(s)$$
$$\frac{V_{OUT}(s)}{VIN(s)}=\frac{\frac{1}{sRC}}{1+\frac{1}{sRC}}$$
$$G(s)=\frac{1}{sRC+1}$$
はい。終わりです。これがRC回路の伝達関数です。
ちなみにこの伝達関数をpspice for tiでシミュレーションしました。良かったらこちらの記事を読んでみて下さい。
この式どうやって使うの?
RC回路の伝達関数はわかったけどさ、これどうやって使うんよ?って話ですよね。それは最初のモチベーションのところに戻ります。
「時間tにおける出力vout(t)を求めるのに使う!!」
え?でも周波数領域だから時間領域のことわからんじゃん。って思うかもですが、逆変換が出来ます。
$$G(s)=\frac{1}{sRC+1}$$
これをラプラス変換表を見ながら逆変換すると、、、すぐには出来ないので、ちょっと式変形します。
分子分母をRCで割って
$$G(s)=\frac{\frac{1}{RC}}{s+\frac{1}{RC}}$$
分母のところをちょっと弄る。
$$G(s)=\frac{1}{RC}\frac{1}{s-(-\frac{1}{RC})}$$
これで変換表のNo4が適用できますね。逆変換します。
$$\frac{v_{out}(t)}{v_{in}(t)}=\frac{1}{RC}e^(-\frac{t}{RC})$$
つまり時間tにおける出力vout(t)は以下の式で計算できるということになります。
$$v_{out}(t)=\frac{1}{RC}e^{(-\frac{t}{RC})}v_{in}(t)$$
かんたんに解く方法
さいごにより簡単に解く方法を紹介しておきます。Cを1/sCのインピーダンスと見なして回路を書き直してVOUTを求めると伝達関数が一撃で求まります。
先ほどの回路をC->1/sCに書きなおしてみます↓。

RはそのままでCは1/sCというインピーダンス成分と見なします。あとは超簡単です。
VOUT(S)=の式を作ります。VOUT(s)はVIN(s)をRと1/sCの分圧で出来ています。なので
$$VOUT(s)=\frac{\frac{1}{sC}}{R+\frac{1}{sC}}*VIN(s)$$
分子分母にsCを掛けて綺麗にします。
$$VOUT(s)=\frac{1}{sRC+1}*VIN(s)$$
伝達関数=出力(s)/入力(s)なので両辺をVIN(s)で割ります。
$$G(s)=\frac{VOUT(s)}{VIN(s)}=\frac{1}{sRC+1}$$
はい。これで終わりです。
本日は以上になります。
誰かの参考になれば幸いです。最後までお読みいただきありがとうございました!!!