みなさん、エクセルでボード線図描いていますか?
あなたの近くに周波数特性をエクセルで書いてる人っていませんか?
一番左列に周波数をわーって書いて、Gain(利得)を求めるために伝達関数をゴリンゴリンに解いて実部と虚部に分けて~みたいに。
私も古典制御を学びたてのころはやってましたよ。伝達関数解いて、エクセルでボード線図描いてみて、「ふぅ~~ん。想定したボード線図と同じだぁ。」って。
でもね、1回やったらいいんすよ。そういうのは。いや計算を解けるのはすごいよ。。。すごいんだけど、、、ねえ。。でも、パソコンにやらせたらすぐですやん。って思います。
「そうは言ってもパソコンにやらすのにも勉強がいるじゃんか。制御の勉強をするのにプログラミングも勉強せないかんのか!!」という方もおられるかと思います。
今日はですね。そういった方がPI制御の周波数特性をエクセルで書きたい!という、とてもニッチな欲望を解決しようと思います。
具体的にはPI制御の伝達関数を実部と虚部に分ける計算をしてみようと思います。しんどいんだこれが。
私の本音としては
1回はやってみてもいいけど何回もやるのは時間の無駄!!!MatlabとかPythonとかで解け!!!!これ読みんさい!!!!
本で買うなら2860円。これで勉強するだけで一生、伝達関数を実部と虚部に分けなくて済みますよ。
と本記事を否定しましたが、まぁやってみようと思います。
結論
先に結論です。離散時間系のPI制御器の伝達関数はゲインと実部と虚部は以下の式で表されます。
$$20log(|G(s)|)= 10log(Re^2+Im^2)$$
$$Re=Kp + \frac{Ki}{2}$$
$$Im=-\frac{1}{2}*Ki*\frac{1}{tan(\frac{2\pi{}f}{f}\frac{1}{2})}$$
こうなります。と言っても「ほんとに~?」と納得できないですよね。
まぁとりあえずボード線図みたい人はこれをエクセルに打ち込んでボード線図描いてみて下さい。
PI制御とは?
まずはPI制御って何?を考えてみましょう。比例制御+積分制御ですね。まぁこういうブロック線図です。まずは連続時間で考えます↓。∫部分が連続時間だよですね。
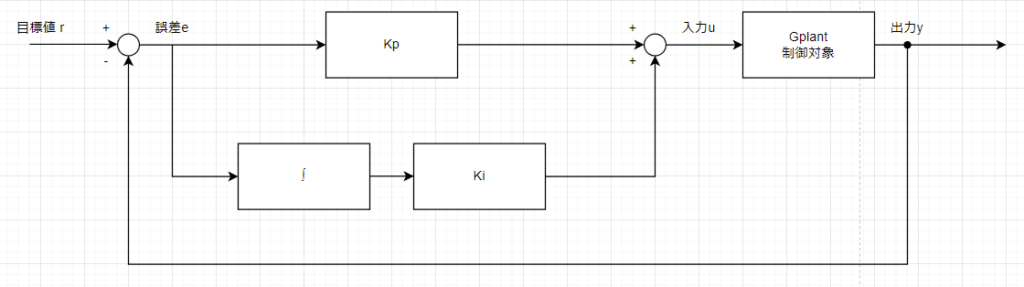
ラプラス変換表を見ながら、ラプラス変換するとまぁこうですね↓。

そのときの伝達関数はまぁ単純にこうです↓。単純な話ですね。
$$G_{pi}(s)=K_p+\frac{1}{s}*K_i$$
PI制御の周波数特性をざっくり考える
さてここでPI制御器の周波数特性を考えましょう。ちょっと式を変形します。まずK_pで括ります。
$$G_{pi}(s)=K_p(1+\frac{\frac{K_i}{K_p}}{s})$$
$$\frac{K_i}{K_p}=T_i$$
とします。
$$G_{pi}(s)=K_p(1+\frac{T_i}{s})$$
つぎに()内を分数だけにします。
$$G_{pi}(s)=K_p(\frac{s+T_i}{s})$$
さて、この伝達関数を見て000ボード線図を想像しましょう。どうなるでしょうか?
分母=0となる周波数がポール周波数です。分母はsなので、0Hz時点にポールがいることになります。
また分子=0となる周波数がゼロ周波数です。
$$s+T_i=0$$
$$s=-T_i$$
$$jω=-T_i$$
$$j2\pi f=-T_i$$
$$f=-\frac{T_i}{j2\pi}$$
どういう理屈か忘れましたが、周波数が負っつーことはないので、正の値にします(おいおい)。まぁちゃんと理屈を追っかけたら正の値になるはずです。
$$f=\frac{T_i}{2\pi}$$
つまり0Hzからポールがあって、Ti/2πHz時点でゼロ点がいるって感じですね。絵にするとこんな感じです↓。
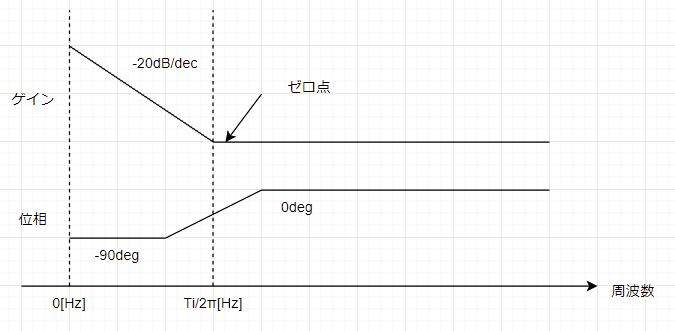
これは連続時間系の話ですが、この特性は離散時間系でも変わりません。ゼロ点周波数が変わりますが、0Hzで-20dB/decで落ちて行って、ゼロ点でバキッと真っ直ぐになるのは変わりません。
ADコンバータで値を取ってぇ、デジタル回路でごちゃごちゃ計算してぇってやってるタイプは離散時間系です。
離散時間系PI制御を考える
さきほどまでは連続時間系の話です。離散時間系だと∫がΣになります↓。
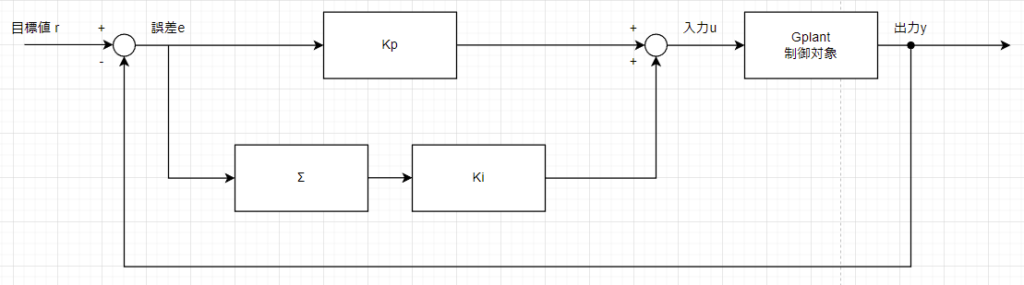
↑においてT周期ごとに加算していく加算器がΣです。N回目のPI制御器出力u[n]はどうなるかをブロック線図を見ながら式にしてみましょう。
$$u[n]={K_p*e[n]+K_i*T\sum_{0}^{n}e[n]}$$
離散時間系はZ変換します↓。ラプラス変換の離散時間版がZ変換です。Z変換はz=e^stとすると変換できます。(理屈は知らん。)
Z変換表を見ながらZ変換します。ΣのZ変換ってどうやるの?はここ見ながらやりました。
$$U[z]=K_p*E(z)+\frac{K_i}{1-z^{-1}}*E(z)$$
伝達関数の形にします。つまり出力/入力の形にします↓。まぁE(z)で割ります。
$$G(z)=K_p+ \frac{K_i}{1-z^{-1}}$$
これを周波数領域に持っていきます。z^-1=e^(-sT)とすることで置き換えれます。
$$G(s)=K_p+\frac{K_i}{1-e^{-sT}}$$
これが離散時間系PI制御器の伝達関数です。
さて、先ほどと同様に伝達関数を弄って、ボード線図がどうなるかを考えましょう。
まずはKpで括ります。
$$G(s)=K_p(1+\frac{\frac{K_i}{K_p}}{1-e^{-sT}})$$
Ki/Kp=Tiとします。
$$G(s)=K_p(1+\frac{T_i}{1-e^{-sT}})$$
つぎに()内を分数だけにします。
$$G(s)=K_p(\frac{1-e^{-sT}+T_i}{1-e^{-sT}})$$
さて伝達関数が分数の形になったので、ポールとゼロ周波数を求めましょう。
まずは、ポール。分母=0で求められます。
$$1-e^{sT}=0$$
$$e^{sT}=1$$
両辺を自然対数logeを付けます。
$$log_e(e^{sT})=log_e(1)$$
$$sT=0$$
つまりポールは0Hzですね。次にゼロ点です。
$$1-e^{-sT}+T_i=0$$
$$e^{-sT}=1+T_i$$
両辺を自然対数logeを付けます。
$$log_e(e^{-sT})=log_e(1+T_i)$$
$$-sT=log_e(1+T_i)$$
$$s=-\frac{log_e(1+T_i)}{T}$$
s=jωなので
$$jω=-\frac{log_e(1+T_i)}{T}$$
ω=2πfなので
$$j2πf=-\frac{log_e(1+T_i)}{T}$$
$$f=-\frac{log_e(1+T_i)}{j2πT}$$
ん~これたしか-が消えるはず。どういう理屈で-が消えるんだっけな。。。まぁとにかく負が消えます。(おいおい)
$$f=\frac{log_e(1+T_i)}{2πT}$$
ですね。これをボード線図にするとこうです↓。
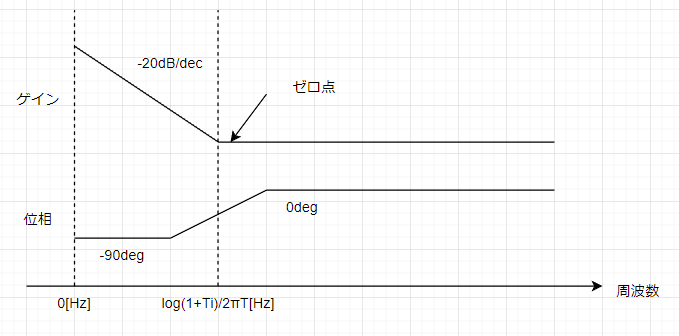
エクセルでやる必要がない人はここで終了です。matlabやらpythonやらでbode(G)とコマンド打ったら一撃でボード線図が出てきますので、確かめてみて下さい。
しかしながら以下はエクセルでやりたい!!という変態向けです。やってみましょう。
離散時間系PI制御伝達関数を実部と虚部に分ける計算をする
まずs=jωなので代入します。
$$G(s)= K_p+\frac{K_i}{1-e^{-jωT}} $$
ここでオイラーの公式↓を使ってe^jωTを変換します。
$$e^{iθ}=cosθ+isinθ$$
$$ G(s)= K_p+\frac{K_i}{1-(cos(-ωT)+jsin(-ωT))}$$
次に負角の公式を使います↓。
$$sin(-θ)=-sinθ$$
$$cos(-θ)=cosθ$$
$$G(s)=K_p+\frac{K_i}{1-(cos(ωT)-jsin(ωT))}$$
分母の()を展開します。
$$G(s)=K_p+\frac{K_i}{1-cos(ωT)+jsin(ωT)}$$
では分母の虚数を消しに行きましょう。分子分母に1-cos(ωT)-jsin(ωT)を掛けます。
$$G(s)=K_p+\frac{K_i*(1-cos(ωT)-jsin(ωT))}{(1-cos(ωT)+jsin(ωT))*(1-cos(ωT)-jsin(ωT) )}$$
地道に展開します。
$$G(s)=K_p+\frac{K_i*(1-cos(ωT)-jsin(ωT))}{1-2cos(ωT)+cos^2(ωT)-j^2sin^2(ωT)}$$
$$G(s)=K_p+\frac{K_i*(1-cos(ωT)-jsin(ωT))}{1-2cos(ωT)+cos^2(ωT)+sin^2(ωT)}$$
ややこしくなってきたので、分母だけ見ます。
$$分母= 1-2cos(ωT)+cos^2(ωT)+sin^2(ωT) $$
三角関数の公式からsin^2+cos^2=1なので、
$$分母= 2-2cos(ωT)$$
すっきりしたので戻します。
$$G(s)= K_p+\frac{K_i*(1-cos(ωT)-jsin(ωT))}{ 2-2cos(ωT) }$$
さぁあとちょっとです。実部と虚部に分けましょう。
$$G(s)=K_p+\frac{K_i}{2}-j\frac{K_i*sin(ωT}{2(1-cos(ωT))}$$
実部が出ましたね↓。
$$Re=Kp + \frac{Ki}{2}$$
もう一工夫で虚部だけ見ましょう。
$$Im=-\frac{K_i*sin(ωT}{2(1-cos(ωT))}$$
倍角の公式を使う準備をします。
$$Im=-\frac{K_i*sin(2*\frac{ωT}{2}}{2(1-cos(2*\frac{ωT}{2}))}$$
とりあえず、ややこしいのでωTpwm/2=θとします。
$$Im=-\frac{K_i*sin2θ}{2(1-cos2θ)}$$
$$Im=-\frac{K_i}{2}\frac{sin2θ}{1-cos2θ}$$
さぁ倍角の公式を使いましょう。
$$sin2x=2sinxcosx$$
$$cos2x=2cos^2x-1=1-2sin^2x$$
$$Im=-\frac{K_i}{2}\frac{2sinθcosθ}{1-(1-2sin^2θ)}$$
$$Im=-\frac{K_i}{2}\frac{2cosθ}{2sinθ}$$
$$Im=-\frac{K_i}{2}\frac{cosθ}{sinθ}$$
ありゃーシンプルになりましたね。さらにシンプルにできます。
$$tanθ=\frac{sinθ}{cosθ}$$
$$Im=-\frac{K_i}{2}\frac{1}{tanθ}$$
θ=wTpwm/2なので元に戻します。
$$Im=-\frac{K_i}{2}\frac{1}{tan(\frac{ωT}{2})}$$
はい。伝達関数に戻しましょう。
$$G(s)=K_p+\frac{K_i}{2}-j\frac{K_i}{2}\frac{1}{tan(\frac{ωT}{2})}$$
G(s)の絶対値は実部と虚部の二乗を足した√です。
$$|G(s)|=\sqrt{Re^2+Im^2}$$
んで、ゲインをdB表記にするには20log|G(s)|です。
$$20log|G(s)|=20log(\sqrt{Re^2+Im^2})$$
√は^(1/2)のことでlogの前に出せます。だから
$$20log|G(s)|=10log(Re^2+Im^2)$$
はい。これで最初の結論に出てきた式が全て出てきました。以上で終わりです。
どうでした?しんどくなかったですか?私はとてもしんどかったです。
最後に
皆様、こんなことせずにパソコンに計算させる方法を学びましょう。終わりです。
誰かの参考になれば幸いです。最後までお読みいただきありがとうございました!!!!