【電子回路】絶縁DCDCでよく見る負帰還回路の補償器について

みなさま、お疲れ様です。

本日は絶縁DCDCでよく見る負帰還回路の位相補償設計方法について解説してみようと思います。

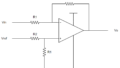
絶縁DCDCの回路でよく見ますよね。こんな感じ↓。シャントレギュレータとフォトカプラで構成されているような感じの。

この赤枠の位相補償R、Cってどう設定したらいいの？

とお悩みの方の参考になれば幸いです。

結論を言ってしまえば、「このRC回路でPI制御のゼロ点周波数fzを決めてる。fz=1/2πRCで狙いのfzに決めればよい。」です。

では始めます。

まず動きのイメージを掴む

そもそもこれってどう動くの？という方に向けてイメージを解説してみます。

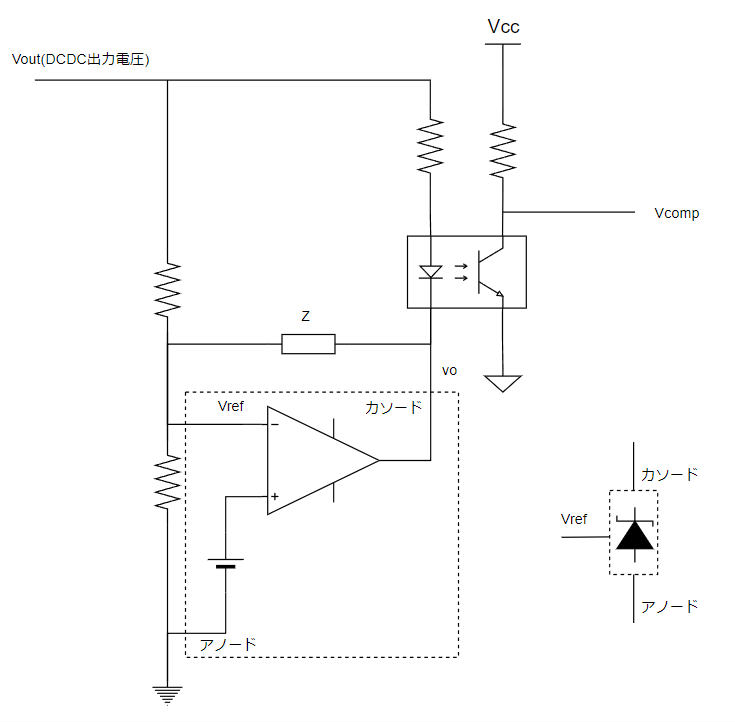
シャントレギュレータの中身をもうちょい詳しく描くと以下の通りです。

これでDCDCの出力電圧が大きくなったとき、小さくなったときにVcompがどう動くのか？を考えてみます。

順番に考えると以下のようになります。

つまり「DCDC出力電圧が大きくなるとVcompが小さくなる。」です。

PWM制御コントローラーはだいたいVcompが小さくなるとスイッチングDutyを下がるので、結果的にDCDC出力電圧が下げる方向に制御していることになります。

「DCDC出力電圧が大きくなると、DCDC出力電圧が小さくなるようにしようとしている。」ということです。

まぁ先ほどの逆なのですが、順番に考えると以下のようになります。

つまり「DCDC出力電圧が小さくなるとVcompが大きくなる。」です。

なので、「DCDC出力電圧が小さくなると、DCDC出力電圧が大きくなるようにしようとしている。」ということです。

これで出力電圧を安定させることが出来ます。

位相補償RCは結局PI制御のゼロ点です。では、なぜそうなのか？を考えてみます。

詳しい導出方法は過去にTyp3補償器で導出しているのと同じです。こちらも良かったら読んでみて下さい。

シャントレギュレータの入出力電圧に注目すると、入力電圧を大きくすると出力電圧は小さくなります。

ということは、シャントレギュレータは等価的にオペアンプで以下のように置き換えれます。

RCのインピーダンスZで負帰還返されているオペアンプとなります。インピーダンスZは

$$\small{
Z=R+\frac{1}{sC}\\
Z=\frac{1+sRC}{sC}
}$$

です。

これをvoに注目して、小信号解析します。小信号解析解析は要するにほんの少し振動したら出力電圧どうなるの？って解析です。

小信号解析するときはDC成分を無視します。つまり、もう電源もGNDも一定電圧は0Vと見なします。

思い切って出力電圧とGNDを繋げて、VrefもDC電圧だからGNDに繋げます。

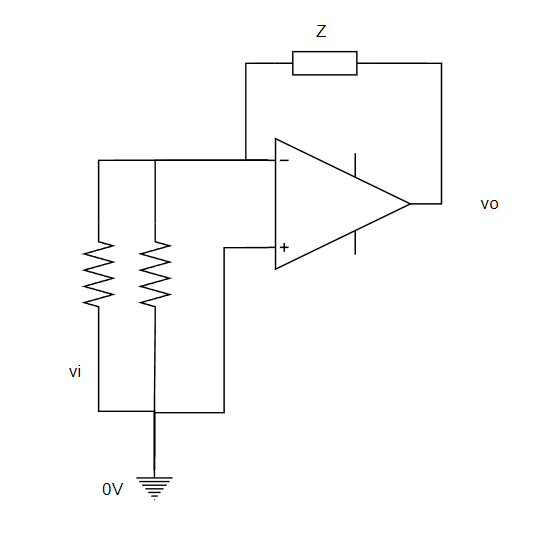
Rをまとめて、Z1とします。そして入力電圧が揺れたときを考えます。

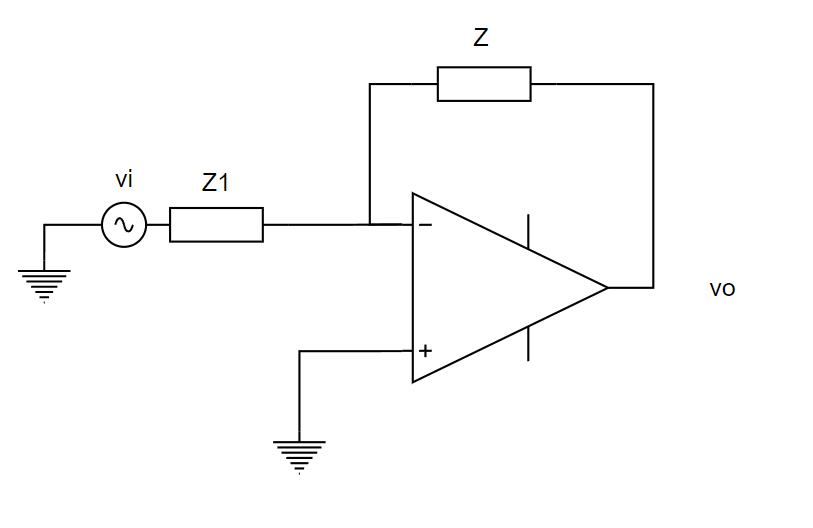
ここでオペアンプの負帰還を返していたら発生する現象の「イマジナリーショート」を使います。これを使うとオペアンプの入力電圧が同じになるという現象です。

つまり、こうです↓。

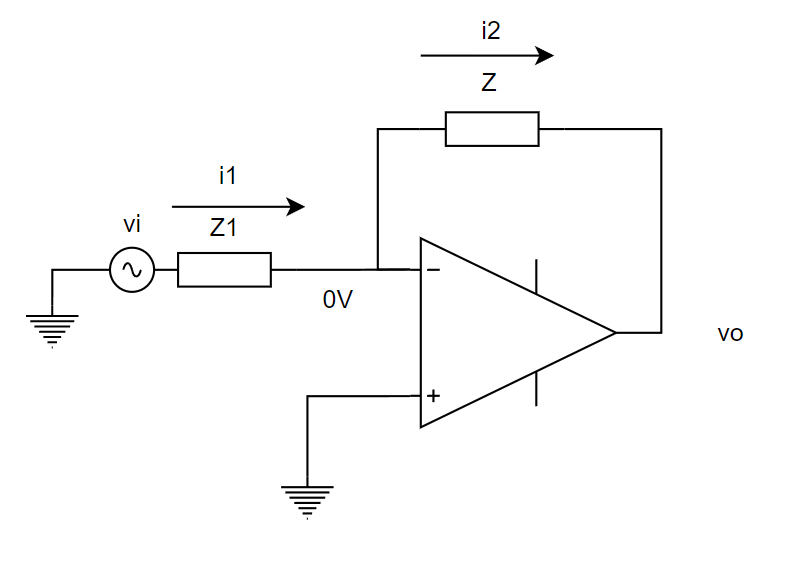
キルヒホッフの法則からi1=i2となります。

$$\small{
i_1=i_2\\
\frac{v_i-0}{Z_1}=\frac{0-v_o}{Z}\\
}$$

これを整理すると

$$\small{
\frac{v_o}{v_i}=-\frac{Z}{Z_1}\\
\frac{v_o}{v_i}=-\frac{1+sRC}{sZ_1C}
}$$

この伝達関数を見ると、ボード線図はこんな感じです。

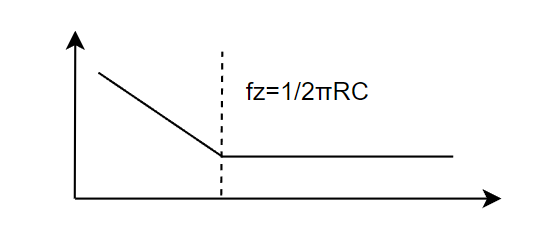
分母にsがあるから、最初は20dB/decで落ちて、分子に1+sxがあるから、折れ点周波数でゼロ点がある感じです。

そのゼロ点は先ほどの導出の通り、RCで決まります。

つまりプラント伝達関数に応じて、ゼロ点を配置したい周波数にRCを当てはめたら良いよ。という話でした。

以上で本記事は終わります。誰かの参考になれば幸いです。最後までお読みいただきありがとうございました！！！