【PFCコンバータ】トーテムポール型ブリッジレスPFCコンバータの電流制御設計方法を解説

みなさま、お疲れ様です。

本日は「トーテムポール型ブリッジレスPFCコンバータ」の電流制御の設計方法を解説してみようと思います。

という方の参考になれば幸いです。今回は電流制御のみに絞って解説します。では、始めます。

制御イメージ

やりたいことは“リアクトル電流ILを正弦波にしつつ、出力電圧を一定にすること”です。

具体的なブロック線図が以下です↓。

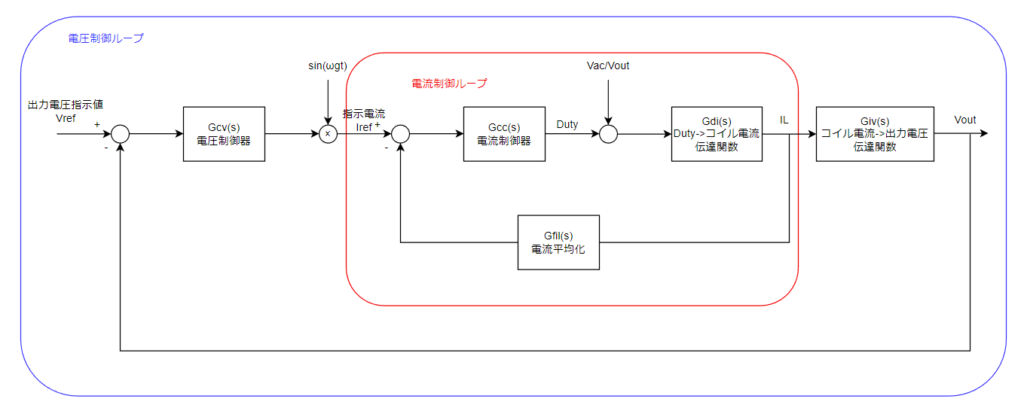
出力電圧Voutを制御器Gcv(s)で制御します。その制御器の出力が電流制御の指示値となります。

それを正弦波にしたいよ。ってのがそもそもやりたいことなので、sin(ωt)を掛けて正弦波の指示電流にします。

それとリアクトル電流ILのフィードバックと比較して、Gcc(s)で制御します。

その出力にVac/Voutを足し算します。これが入力電圧Vacが正弦波で変化する影響を消すためのフィードフォワードになります。リアクトル電流のギザギザが0Aに当たってしまう領域を持ち上げて、より正弦波に近づけます。

ざざっと言うとこんな感じです。今回は正弦波電流指示値を入力して、リアクトル電流が正弦波にするまでを解説してみようと思います。

電流プラント伝達関数Gdi(s)の導出

まずは制御対象の特性を考えます。ブロック線図上のGdi(s)です。

伝達関数を導出するうえで、トーテムポール型ブリッジレスPFCコンバータの動作は昇圧コンバータと同じと考えたら理解出来やすいと思います。

入力電圧Vacの正弦波で上側半サイクルと下側半サイクルは同じなので、上側半サイクルで考えます。

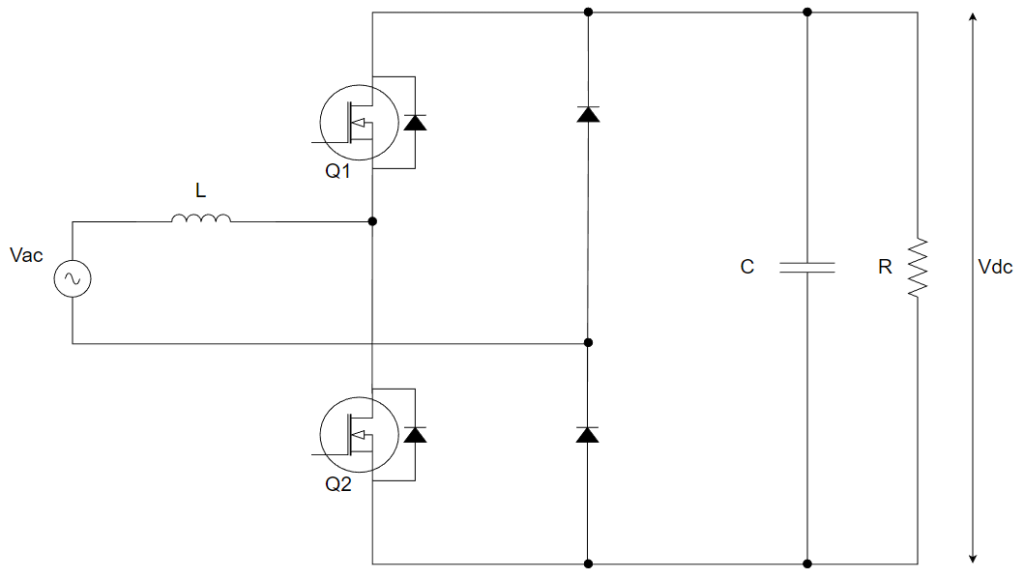
まず、Q1=OFF,Q2=ONのときを考えます。回路図は以下です。

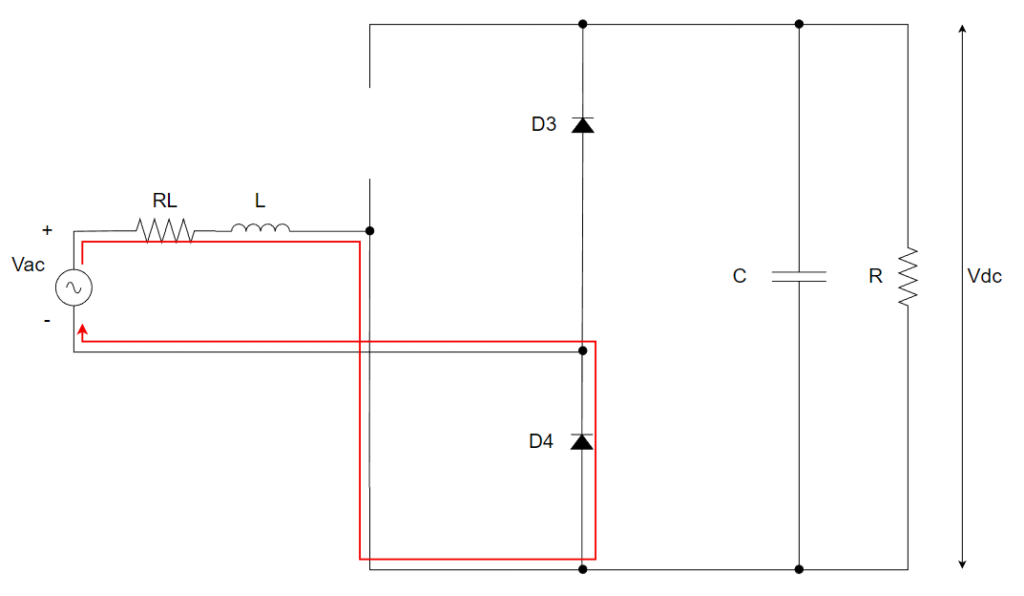
これをちょっとわかりやすいように昇圧コンバータっぽく書き換えます。

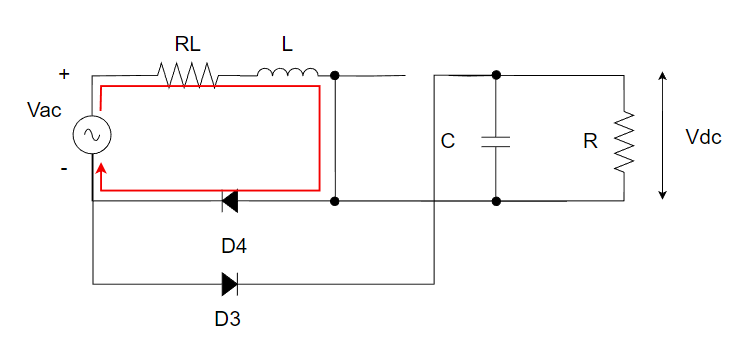
このときの電圧と電流の関係式を立てます↓。

$$\small{
V_{ac}=R_Li_L(t)+Li_L'(t)\\
i_L'(t)=-\frac{R_L}{L}i_L(t)+\frac{1}{L}V_{ac}
}$$

ラプラス変換すると以下です。微分にsを付けるだけです。

$$\small{
sI_L(s)=-\frac{R_L}{L}I_L(s)+\frac{1}{L}V_{ac}
}$$

つぎにQ1=ON,O2=OFFのときを考えます。回路図は以下です。

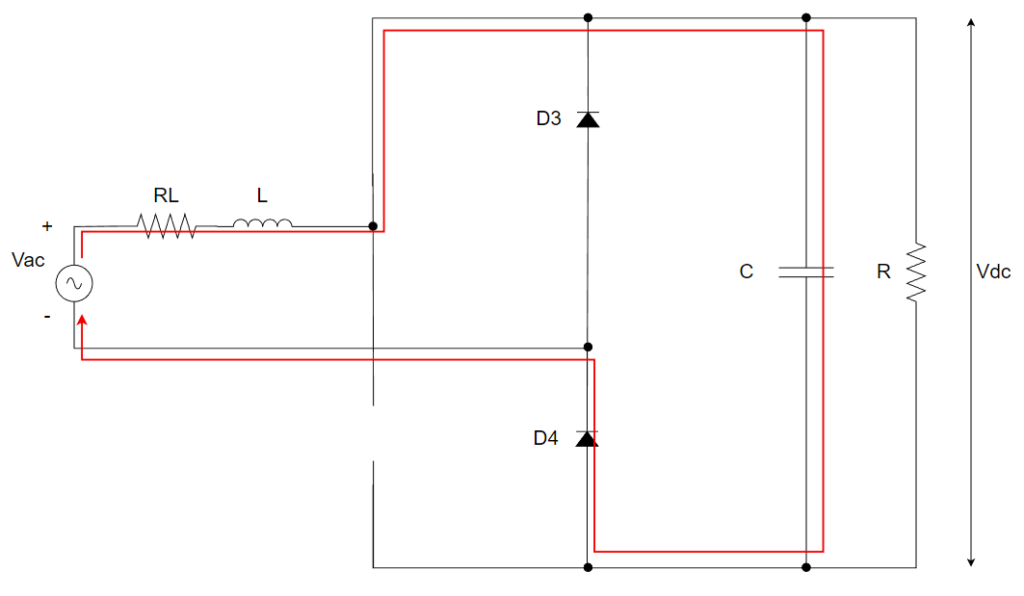
これをちょっとわかりやすいように昇圧コンバータっぽく書き換えます。

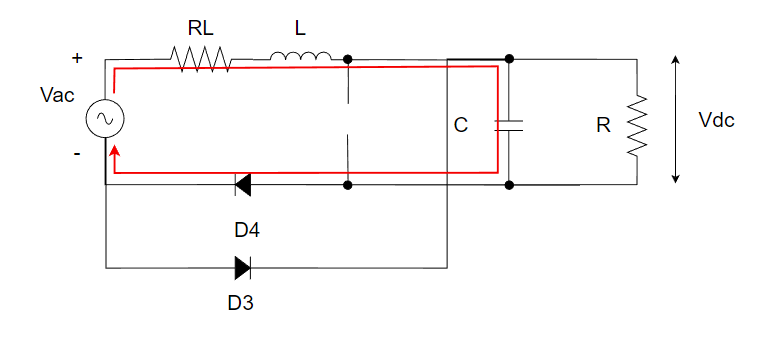
このときの電圧と電流の関係式を立てます↓。

$$\small{
V_{ac}-V_{out}=R_Li_L(t)+Li_L'(t)\\
i_L'(t)=-\frac{R_L}{L}i_L(t)+\frac{1}{L}(V_{ac}-V_{out})
}$$

ラプラス変換すると以下です。微分にsを付けるだけです。

$$\small{
sI_L(s)=-\frac{R_L}{L}I_L(s)+\frac{1}{L}(V_{ac}-V_{out})
}$$

これらをDutyで平均化します。

$$\small{
sI_L(s)=-\frac{R_L}{L}I_L(s)+\frac{1}{L}(V_{ac}-Duty(s)V_{out})
}$$

これを”IL(s)=”の形にします。

$$\small{
\left(s+\frac{R_L}{L}\right)I_L(s)=\frac{1}{L}V_{ac}-\frac{1}{L}V_{out}Duty(s)
}$$

Vacは固定値として消します。

$$\small{
\left(s+\frac{R_L}{L}\right)I_L(s)=-\frac{1}{L}V_{out}Duty(s)
}$$

Gdi(s)=IL(s)/Duty(s)=の形にします。

$$\small{
\frac{I_L(s)}{Duty(s)}=-\frac{1}{\left(s+\frac{R_L}{L}\right)L}V_{out}\\
G_{di}(s)=\frac{I_L(s)}{Duty(s)}=-\frac{V_{out}}{sL+R_L}
}$$

この式をみると、周波数特性が以下のようなイメージになると分かります。

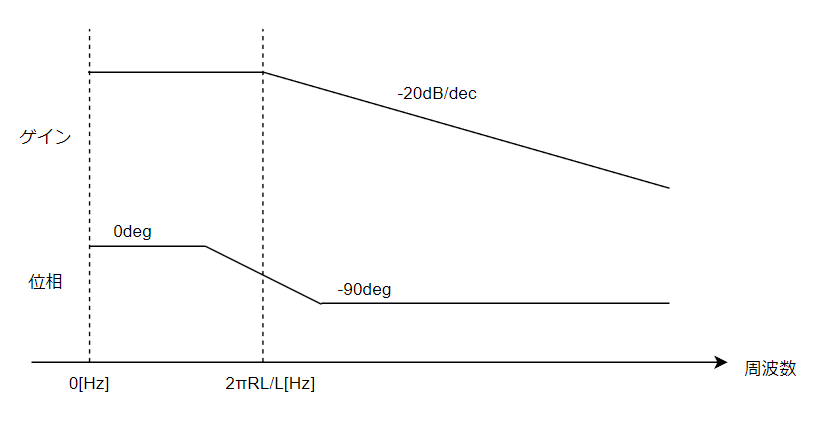
RLはリアクトルの直列抵抗なので、値としてはmΩオーダーで非常に小さいです。なので非常に低域に極周波数があります。

最初から位相が-90deg回って、ずっと-20dB/decで落ちていくと近似することも出来ます。

電流制御部の周波数特性をPSIMで確認

さきほどの式が「ほんとうに？お前がただ思ってるだけだろ。」ってことがあるので、シミュレーションで計算してみます。

PSIMで以下の回路を作って、ACシミュレーションしました。

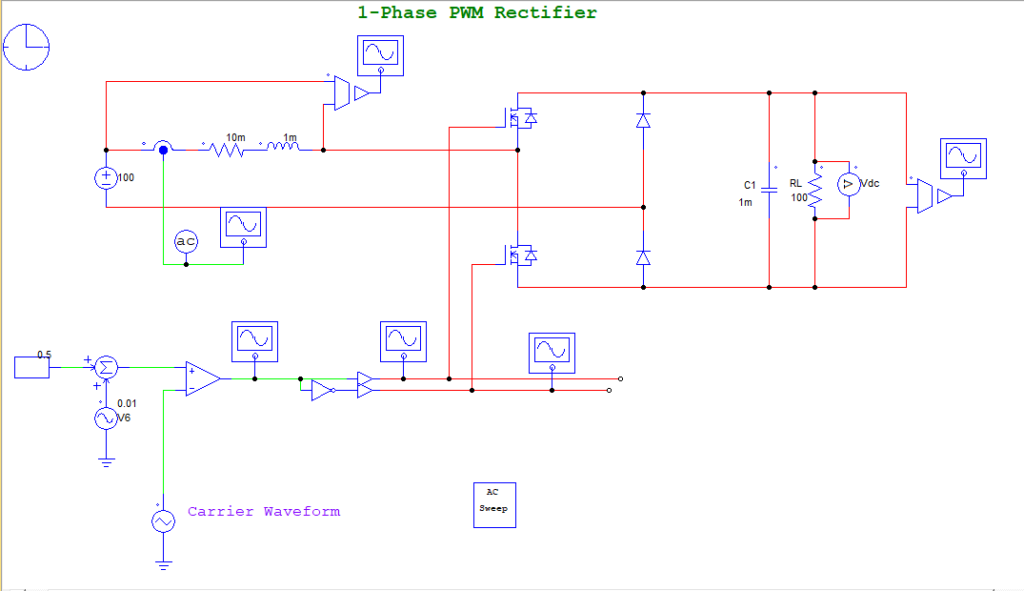
RL=10mΩ、L=1mHです。なので極周波数は

$$\small{
ω=\frac{R_L}{L}=\frac{10m}{1m}=10\\
f=\frac{ω}{2π}=\frac{10}{2π}=1.6Hz
}$$

で、シミュレーション結果が以下となりました。

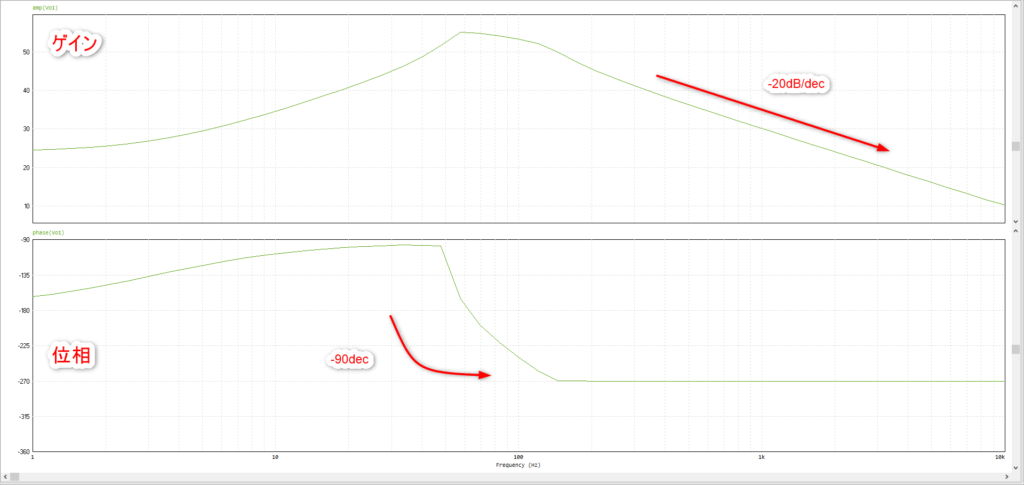
ん～～～？まぁ低域で90deg回ってるのは想定通り。だけど、折れ点周波数はちょっと違いますし、何か二次遅れみたいにふわぁ～と浮いてきてますね。測定方法の影響ですかね。

まぁ、-180degから45deg変化しているのは3Hzくらいなので、そこに極がある感じですかね。

制御ループの設計

さきほどの回路を想定してVac=100VでIL=2Aとして制御設計してみようと思います。なので、3Hzに極周波数がいるって感じですね。近似っつーか想定のボード線図は以下です。

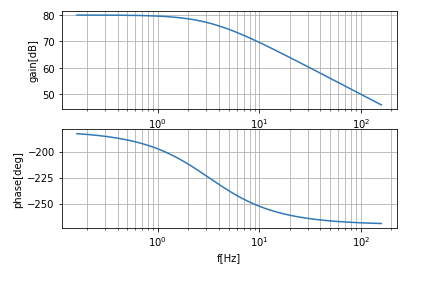
制御はPI制御を適用します。プラントの極周波数にPI制御のゼロ点を当てて、キャンセルします。

そうすると、合成した周波数特性はゲインの落ち込みが-20dB/decで落ち、位相が-90deg回った状態になります。

先ほどの測定結果を信用して、ゼロ点周波数を3Hzに置きます。

$$\small{
f_z=3[Hz]\\
ω_z=2πf_z=18.85\\
Ti=\frac{1}{ω_z}=0.053≒0.05
}$$

なのでPI制御器のTiを0.05とします。ゲインが1になるようにKp=0.05にしたら、ボード線図は以下です。

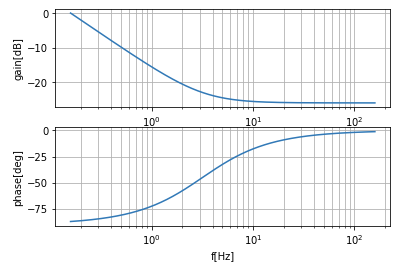
PI制御のゲインを調整して、クロスオーバー周波数をスイッチング周波数の1/10程度になるようにします。ひとまず現時点の合成した周波数特性を見てみます↓。

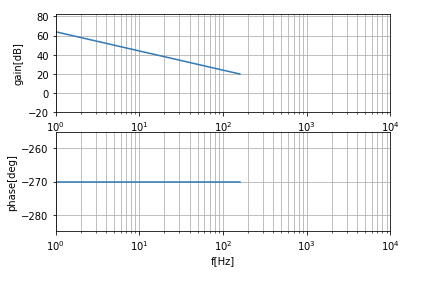
このまま一直線に落ちていってクロスオーバー周波数は1kHzちょいくらいですね。ま、こんなもんか。ってことでこれで動かしてみます。

入力電圧フィードフォワードの効果

さきほどのPI制御定数を設定して、シミュレーションをしてみます。

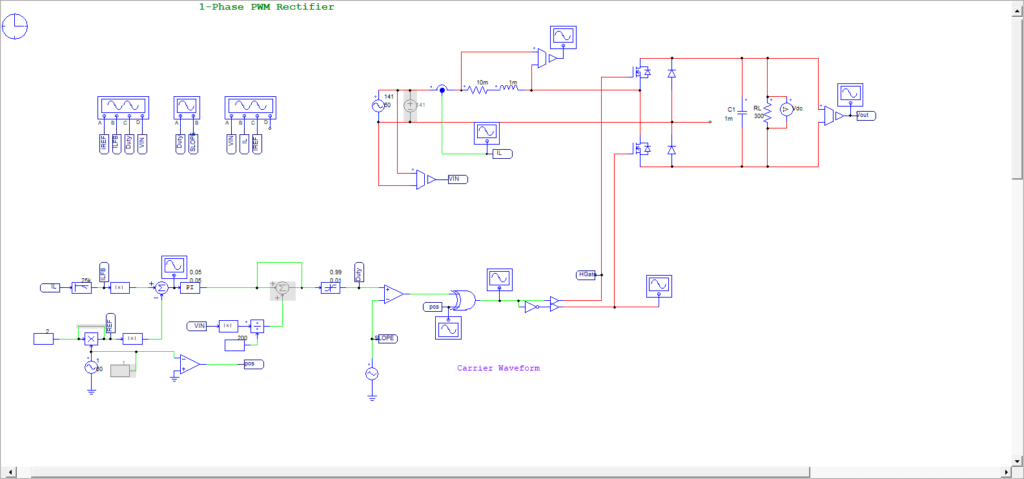
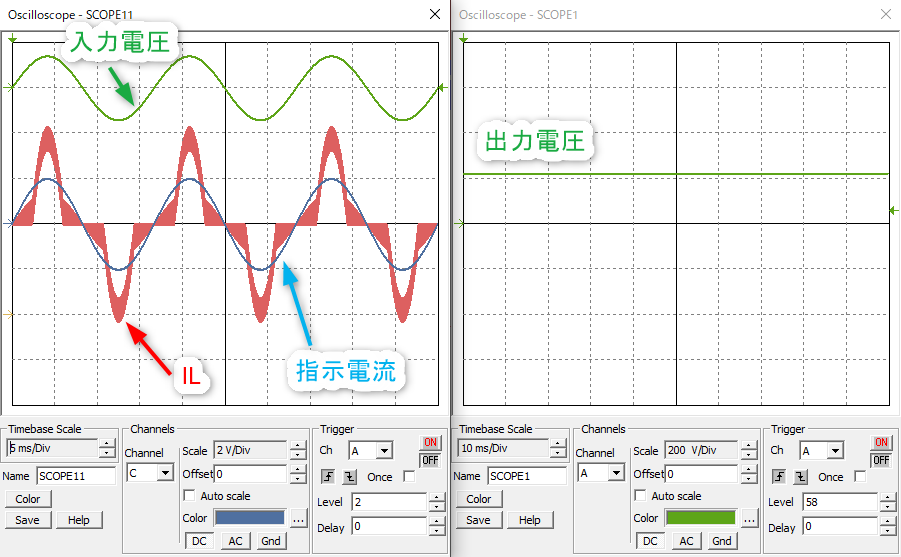
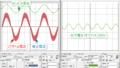
リアクトル電流ILが0Aに近づくとイジャイジャってなってます。それを取り戻そうとACピーク電圧付近でリアクトル電流が行き過ぎてしまってます。

0A付近になるとILが0Aに当たってしまってこの現象が起きてしまいます。入力AC電圧に応じて少しDutyを持ち上げてあげるといい感じになります。

具体的な回路図は以下になります。

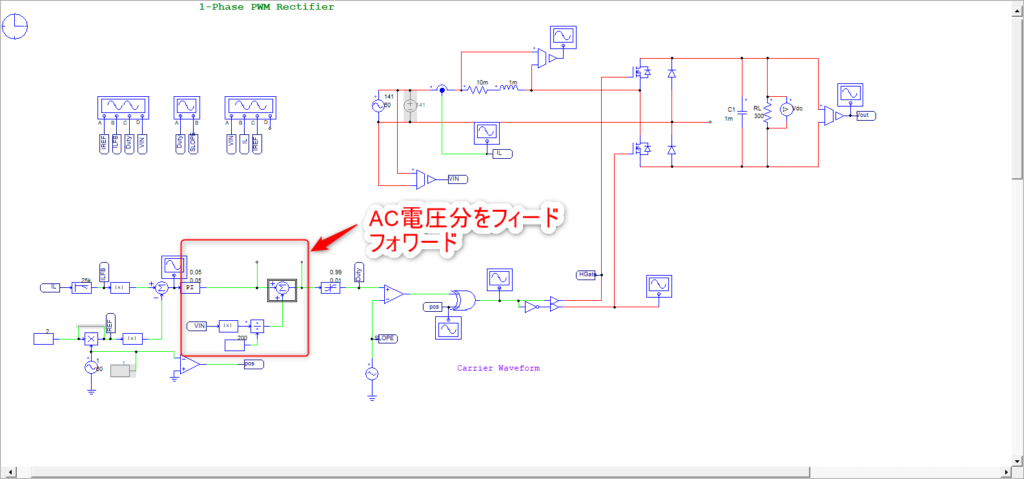
シミュレーション結果は以下です。

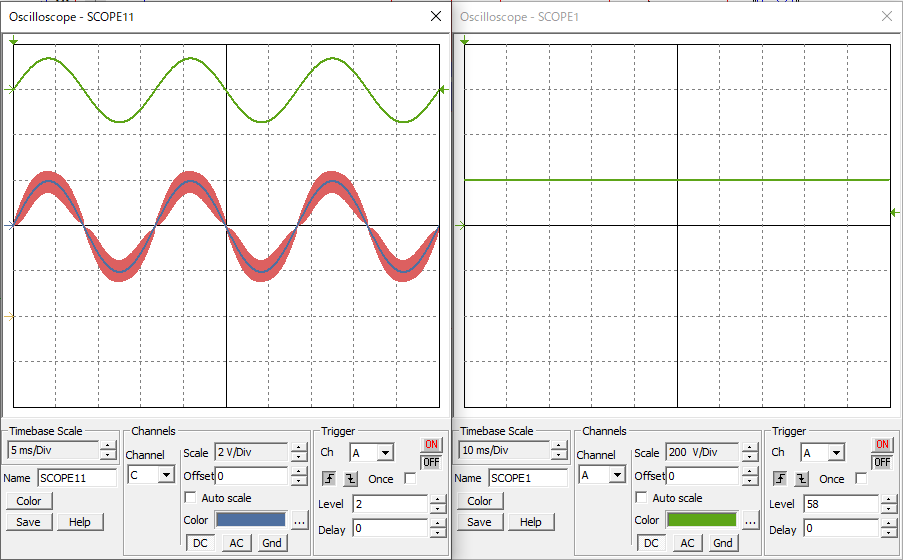
ちゃんとリアクトル電流ILが正弦波になってます。

はい、本記事は以上です。何かの参考になれば幸いです。最後までお読みいただきありがとうございました！！