皆様、お疲れ様です。
LLCコンバータの設計に挑戦中のものです。
これまでの設計経緯
今回はですね。前回計算したプラント伝達関数の周波数応答を描いてみました。
その模様を記録します。
この記事に書いてあること
・Pythonで伝達関数の周波数応答を描く方法
・素人が苦悩する様
ではやってみましょう。
前回導出した伝達関数
これです。
$$Gain=\frac{s^2L_p’R_L’}{\frac{R_L’}{C_r}+\frac{L_p’}{C_r}s+s^2(L_sR_L’+sL_p’R_L’)+s^3L_sL_p’}$$
$$L_s=L_r+\frac{L_pL_r}{L_p+L_r}$$
$$L_p’=L_p-\frac{L_pL_r}{L_p+L_r}$$
$$R_L’=\frac{8}{\pi{}^2}*N^2*R_L$$
これがあってるのか?どうなんでしょうかね?ってのが前回でした。
分子にs^2があるのを見て、うっすらと「何かおかしくね?」と感じていますが、馬鹿なので全く説明ができません。
Pythonを用いてボード線図を描いてみる
コードをね書いてみました。
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym
import control as ctl
Lr = 55e-6
Cr = 0.047e-6
RL = 2.4
N = 7.5
RL_d = 8/np.pi**2*N**2*RL
Ls = Lr+Lp*Lr/(Lp+Lr)
Lp_d = Lp-Lp*Lr/(Lp+Lr)
Gplant = ctl.tf([Lp_d*RL_d,0,0],[Ls*Lp_d,Ls*RL_d+Lp_d*RL_d,Lp_d/Cr,RL_d/Cr])
gain_plant, phase_plant, w = ctl.bode(Gplant, Plot=False)
f = w/2/np.pi
gain_plant_dB = 20*np.log10(gain_plant)
phase_plant_deg = phase_plant * 180/np.pi
fig, ax = plt.subplots(2,1)
ax[0].semilogx(f, gain_plant_dB)
ax[0].set_yticks([-20,0,20,40,60])
ax[0].grid(which = "both", axis = "x")
ax[0].grid(which = "both", axis = "y")
ax[0].set_ylabel("gain[dB]")
ax[1].semilogx(f, phase_plant_deg)
ax[1].set_yticks([-180,-135,-90,-45,0])
ax[1].grid(which = "both", axis = "x")
ax[1].grid(which = "both", axis = "y")
ax[1].set_ylabel("phase[deg]")
ax[1].set_xlabel("f[Hz]")
controlという制御用のモジュールを使って、先ほどの伝達関数を計算して、ctl.bode()でボード線図を計算して、プロットしています。
結果のボード線図が以下です。
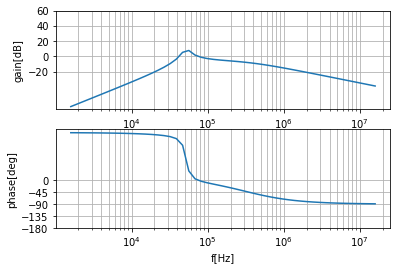
はい。これね。あってるかどうかさっぱりわかりませんね。
最初っから位相が進んでるプラント伝達関数を見たことないけど、うーん。。。ものを知らな過ぎて辛い。
以上です。あーつら。