皆様、お疲れ様です。
LLCコンバータの設計に挑戦中のものです。
これまではパワーデバイス周りをずっと検討していましたが、出力電圧を一定に保つ機能の検討が出来ていませんでした。
今回はLLCコンバータの制御について検討したいと思います。
・LLCコンバータのプラント伝達関数のラプラス変換した式
・その式の導出方法
ではやっていきます。
【結論】こんな感じになりました
$$Gain=\frac{s^2L_p’R_L’}{\frac{R_L’}{C_r}+\frac{L_p’}{C_r}s+s^2(L_sR_L’+sL_p’R_L’)+s^3L_sL_p’}$$
$$L_s=L_r+\frac{L_pL_r}{L_p+L_r}$$
$$L_p’=L_p-\frac{L_pL_r}{L_p+L_r}$$
$$R_L’=\frac{8}{\pi{}^2}*N^2*R_L$$
DCDCにおける制御とは何か
DCDCの役割は一定の電圧を出力することです。
なので
出力電圧>狙い値となったら、出力電圧が小さくなるようにしないといけません。
出力電圧<狙い値となったら、出力電圧が大きくなるようにしないといけません。
だからDCDCは出力電圧をモニターして狙い値との差分を埋めるように動かすことになります。
これがまぁDCDCにおける制御です。
LLCコンバータのプラント伝達関数
定数を決めたときに出てきたGainの式がありました。
$$Gain=\frac{1}{\sqrt{(1+K(1-\frac{1}{F^2}))^2+\frac{1}{Q^2}(F-\frac{1}{F})^2}}$$
これをラプラス変換して周波数解析をしたいと思います。
思いますが、、、
どうラプラス変換したらいいのこれ!!!!????
って思いますね。
まぁ順番に考えていきましょう。
そもそもこの式ってどうやって導出されてるのか?
そもそもこの式はLLCコンバータの等価回路↓から導き出されています。

この等価回路は出力ダイオードが非導通時の等価回路です。
$$L_s=L_r+\frac{L_pL_r}{L_p+L_r}$$
$$L_p’=L_p-\frac{L_pL_r}{L_p+L_r}$$
$$R_L’=\frac{8}{\pi{}^2}*N^2*R_L$$
この等価回路のVoutをガチャガチャ計算していったら、さっきのGainの式が導出されます。
等価回路を簡単にする
立式の時点でラプラス変換して計算してみましょう。
まず等価回路をラプラス変換した形で描いてみます。
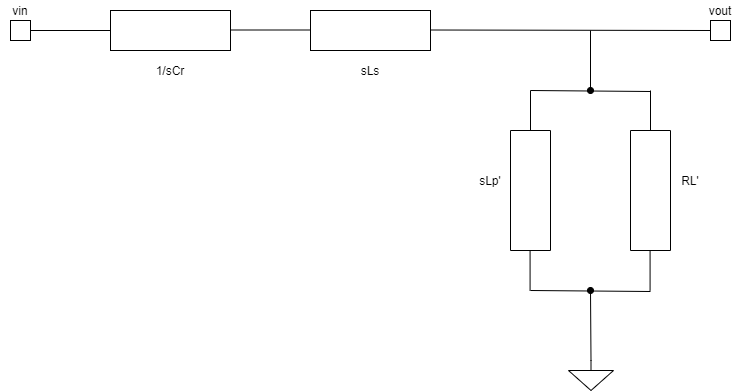
なんかvout=の式が書けそうな感じになりました。
sLp’とRL’が並列の抵抗に見えるので、まとめます。
$$\frac{1}{Z_2}=\frac{1}{sL_p’}+\frac{1}{R_L’}$$
$$\frac{1}{Z_2}=\frac{R_L’+sL_p’}{sL_p’R_L’}$$
ひっくり返します。
$$Z_2=\frac{sL_p’R_L’}{R_L’+sL_p’}$$
CrとLsが直列の抵抗に見えるので、まとめます。
$$Z_1=\frac{1}{sC_r}+sL_s$$
こうすると先ほどの等価回路は以下のように書き換えれます。
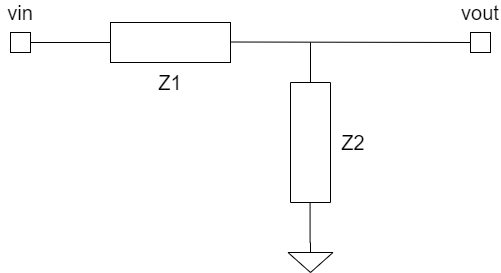
単純な抵抗分圧になりましたね。
出力の式を立式してひたすら解くべし!!
ではvoutの式を立てましょう。
$$v_{out}=\frac{Z_2}{Z_1+Z_2}v_{in}$$
vout/vinがGainなので
$$Gain=\frac{Z_2}{Z_1+Z_2}$$
はい。もう勝ちですね。あとはZ1とZ2を代入して整理しまくればよいだけです。
$$Gain=\frac{\frac{sL_p’R_L’}{R_L’+sL_p’}}{\frac{1}{sC_r}+sL_s+\frac{sL_p’R_L’}{R_L’+sL_p’}}$$
RL’+sLp’を分母分子に掛けます。
$$Gain=\frac{sL_p’R_L’}{(\frac{1}{sC_r}+sL_s)(R_L’+sL_p’)+sL_p’R_L’}$$
分母を展開します。
$$Gain=\frac{sL_p’R_L’}{\frac{R_L’}{sC_r}+\frac{L_p’}{C_r}+sL_sR_L’+s^2L_sL_p’+sL_p’R_L’}$$
整理します。
$$Gain=\frac{sL_p’R_L’}{\frac{R_L’}{sC_r}+\frac{L_p’}{C_r}+s(L_sR_L’+sL_p’R_L’)+s^2L_sL_p’}$$
sを分母分子に掛けます。
$$Gain=\frac{s^2L_p’R_L’}{\frac{R_L’}{C_r}+\frac{L_p’}{C_r}s+s^2(L_sR_L’+sL_p’R_L’)+s^3L_sL_p’}$$
あ~でけた~。疲れた~。
この式がどんな周波数特性(ボード線図)になるでしょうか。
私にはわかりません!!!
また次回やってみます。
終わりです。最後まで読んで頂きありがとうございました!!!


