みなさま、お疲れ様です。
本記事ではフォワードコンバータの動作原理を解説してみようと思います。
- フォワードコンバータの動作が分からない!!!
- 入出力電圧関係式がなんでこの式になるのか分からない!!!
という方の参考になれば幸いです。
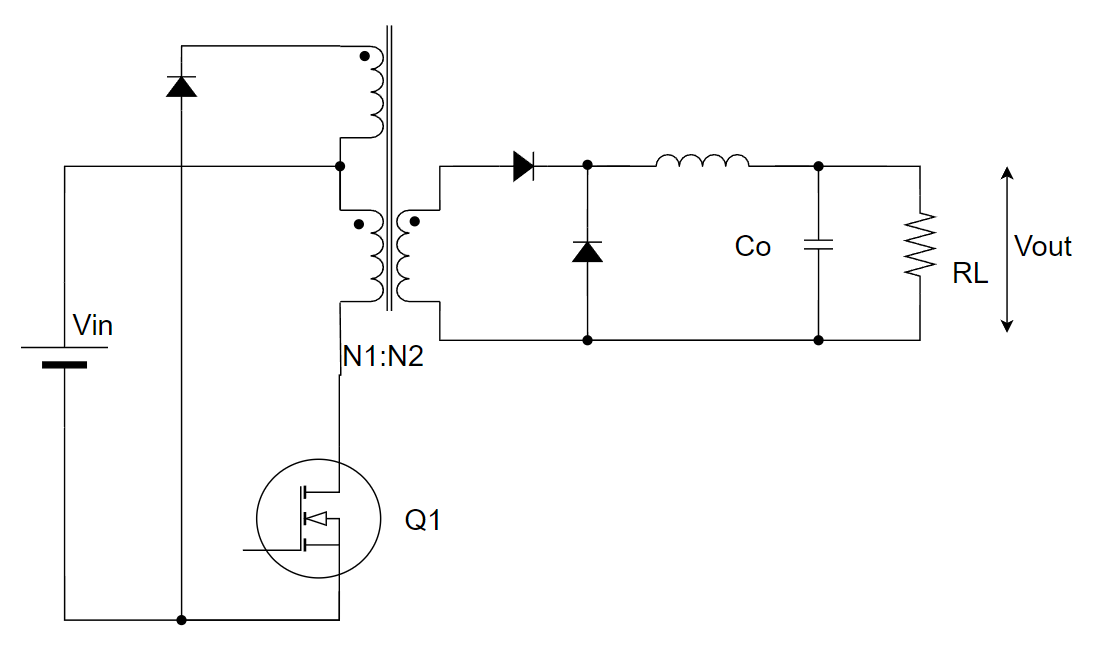
ちなみに回路図はこんな感じですね↓。

磁気リセット回路は巻き上げトランス式について解説します。
動作原理の解説
動作モードは4通りです。
モード1:スイッチがONする
Q1がONしてトランスのn1巻き線にVinの電圧がかかり、励磁電流が流れます。これにより、二次側のn2巻き線に巻き線比の電圧が印可されます。

出力リアクトルに流れる電流ΔILは以下になります。
$$\small{
ΔI_{Lon}=\frac{\frac{N_2}{N_1}V_{in}-V_{out}}{L}T_{on}
}$$
Vin:入力電圧[V]、N2:2次側巻き線数、N1:1次側巻き線数、Vout:出力電圧[V]、L:出力リアクトルインダクタンス値[H]、Ton:ON時間[sec]
モード2:スイッチがOFFして、励磁電流がn3巻き線に転流する。
モード2では、スイッチがOFFします。
しかし、励磁電流は流れ続けようとします。しかし、1次側と2次側には流れる経路がありません。
すると一番流れやすい経路で上側のリセット巻き線n3に励磁電流が転流して流れます。
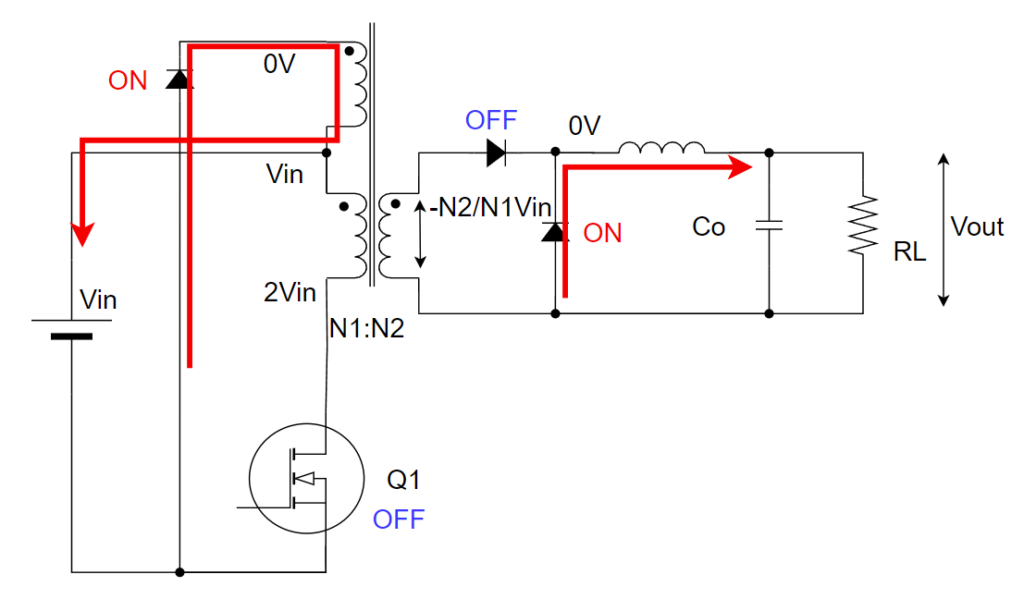
1次巻き線N1と3次巻き線N3の巻き線比は通常同じ比率にするので、同じ電流を流すのに3次巻き線には入力電圧がかかります。
その影響で1次巻き線には-Vinの電圧がかかります。
結果的にスイッチには2Vinの電圧がかかります。
2次側は出力リアクトルに流れていた電流がそのまま流れ続けようとして、下側のダイオードがONして流れます。
出力リアクトルに流れる電流ΔILは以下になります。
$$\small{
ΔI_{Lmode2}=\frac{0-V_{out}}{L}T_{2}
}$$
Vout:出力電圧[V]、L:出力リアクトルインダクタンス値[H]、T2:モード2の時間[sec]
モード3:励磁電流が負になり、1次側電圧が落ち着いていく。
モード2で励磁電流が減少していき、励磁電流が0A以下になったらモード3です。励磁電流はn1巻き線を通って、電源へ流れます。
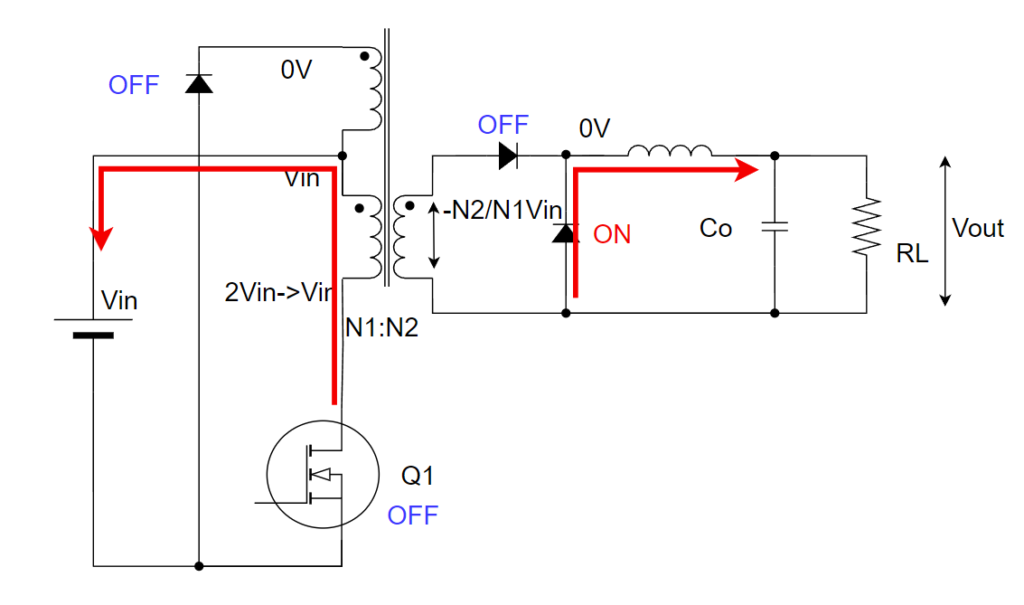
2次側はモード2と変わりません。
出力リアクトルに流れる電流ΔILは以下になります。
$$\small{
ΔI_{Lmode3}=\frac{0-V_{out}}{L}T_{3}
}$$
Vout:出力電圧[V]、L:出力リアクトルインダクタンス値[H]、T3:モード3の時間[sec]
1次側はスイッチ電圧が徐々にVinへ収束していって、モード4になります。
モード4:1次側巻き線電圧が0Vとなり、2次側に励磁電流が流れる。
モード4は1次側巻き線電圧=0Vになる、つまり2次側巻き線電圧も0Vになるため、2次側ダイオードが導通して、励磁電流が流れます。

1次側スイッチ電圧はVinに落ち着きます。
2次側リアクトル電圧はモード2,3,4で変わりません。ずっと同じ状態です。
出力リアクトルに流れる電流ΔILは以下になります。
$$\small{
ΔI_{Lmode4}=\frac{0-V_{out}}{L}T_{4}
}$$
Vout:出力電圧[V]、L:出力リアクトルインダクタンス値[H]、T4:モード4の時間[sec]
入出力電圧関係式
出力電圧はどう計算するか?ですが、これはモード1とモード2,3,4の2つに分けて、2次側リアクトルにかかる電圧に着目したら良いです。
DCDCの鉄則の考え方の
「出力電圧が一定のとき1周期でリアクトルリップル電流ΔILを足し合わせると0Aになる。」
という考え方で解けます。
モード2,3,4のΔILは同じなので、統一してΔIL_OFFとします。
$$\small{
ΔI_{LOFF}=\frac{0-V_{out}}{L}T_{OFF}
}$$
Vout:出力電圧[V]、L:出力リアクトルインダクタンス値[H]、TOFF:スイッチOFFの時間[sec]
これがON時のΔILと足し合わせるとゼロになると出力電圧が安定するので、、、
$$\small{
ΔI_{Lon}+ΔI_{Loff}=0
}$$
これを展開して解いて行きます。
$$\small{
\frac{\frac{N_2}{N_1}V_{in}-V_{out}}{L}T_{on}+\frac{0-V_{out}}{L}T_{OFF}=0
}$$
ON時間の割合をDuty、1周期をTpwmとして書き換えます。
$$\small{
\frac{\frac{N_2}{N_1}V_{in}-V_{out}}{L}Duty T_{pwm}+\frac{0-V_{out}}{L}(1-Duty) T_{pwm}=0
}$$
LとTpwmを消します。
$$\small{
\left( \frac{N_2}{N_1}V_{in}-V_{out}\right) Duty+(0-V_{out})(1-Duty)=0
}$$
頑張ってVout=の形になるように解いて行くと、、、
$$\small{
V_{out}=\frac{N_2}{N_1}V_{in} Duty
}$$
はい、これがフォワードコンバータの入出力電圧関係式です。
これを見ると降圧チョッパに巻き線比が加わっただけじゃん。ってなりますね。
フォワードコンバータはなぜDuty<50%でないとダメなのか?
なんか教科書とかを見ると「一般的にフォワードコンバータはDuty<50%で設計します。」みたいな記述があります。
これはトランスの磁束リセットが要るからですね。ON時にトランスに流れた励磁電流をOFF時にどうにか消費しないといけない。っといったイメージです。消費しきれなかったら次周期に磁束が持ち越され、それが溜まりにたまって磁気飽和となります。
磁気飽和になったらLがめっちゃ小さいトランスになって、スイッチがONした瞬間に電源とGNDがショートしたように電流が流れて非常に危険です。
今回のように1:1の巻き上げトランスのリセット回路を使用していた場合は、リセット時間はON時間と同じになります。なので、最大Dutyはリセットを考えると50%までにしかできないよね。普通に考えて。
ってなります。
しかし、リセット回路はこれだけじゃなくて、RCDリセット回路やアクティブクランプ式のリセット回路があります。こういうのを駆使して、ON時の励磁電流を速く消費してやれば、Dutyを50%以上に太くしても何も問題ないよ。ってなります。
でも100%にはならんすね。リセットがいるから。
シミュレーションで動作確認
「あーはいはい、それってあなたが思ってるだけでしょ?証拠を見せて下さいよ。証拠をね。」
と思う方がいるかもしれないので、シミュレーションで動作を確認してみました。
以下がシミュレーションの回路図です↓。
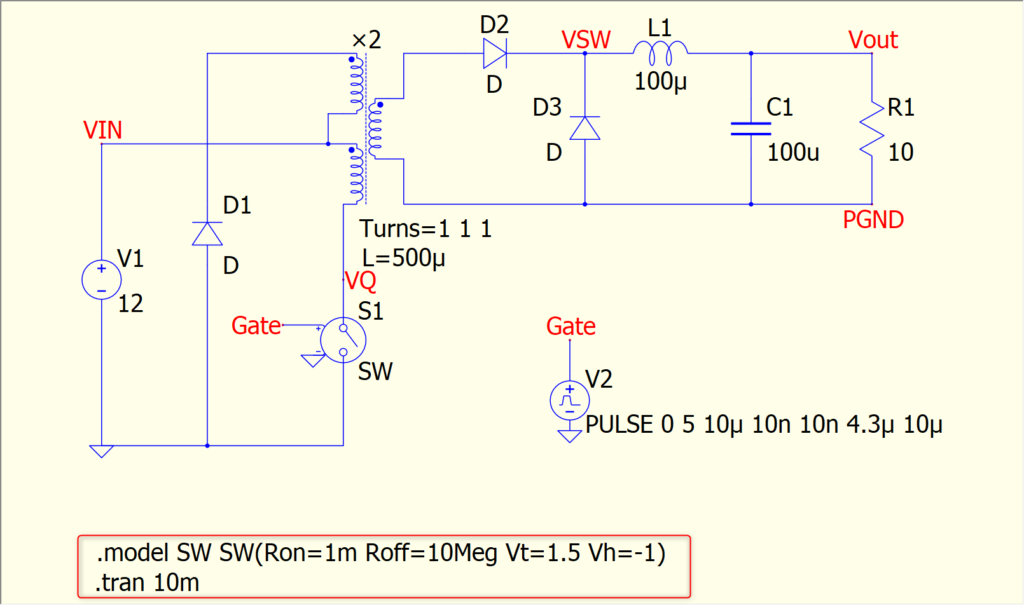
Vin=12Vで1:1のトランスを使って、およそ5Vくらいを出力するくらいのDutyでスイッチを動かします。
そしてシミュレーション結果が以下の通りです↓。

想定通りに動いてますね。モード2で2Vinになってるし、2次側はN2/N1Vinと0Vでスイッチングしてます。
はい、こんな感じで終わります。
誰かの参考になれば幸いです。最後までお読みいただきありがとうございました!!!
参考文献
Active Clamp and Reset Technique Enhances Forward Converter Performance