皆様、お疲れ様です。LLCコンバータを勉強する記事の3回目です。
今回はpythonでLLCコンバータの出力電圧特性を計算するスクリプトを作りましたって小ネタですね。
1回目:【電源回路】LLCコンバータの動作原理
2回目:【電源回路】LLCコンバータはなぜソフトスイッチングするのか?
3回目:【電源回路】LLCコンバータの出力電圧を計算するpythonスクリプト(本記事)
4回目:【電源回路】LLCコンバータの設計手順①(パワーラインの設計編)
5回目:【電源回路】LLCコンバータを周波数可変に修正する
6回目:【電源回路】LLCコンバータの周波数特性を調べる
7回目:【電源回路】LLCコンバータの設計手順②(制御設計編)
8回目:【LLCコンバータ】インターリーブ運転のリップル低減効果を確認する
9回目:【LLCコンバータ】出力電圧Gvf(s)の周波数特性の負荷依存性を調べる
10回目:【LLCコンバータ】マルチレベル方式LLCコンバータの動作原理
11回目:【LLCコンバータ】LLCコンバータの双方向動作について
12回目:【双方向LLCコンバータ】双方向で電圧調整可能なCLLCコンバータについて解説
13回目:【CLLCコンバータ】LLCとCLLCでは、なぜ出力電圧VSスイッチング周波数の特性が違うのか?
Excelで作っても良いですが、定数や負荷電流を変えたパターンを何個も計算したいと思ったときにスクリプトにしておいた方がやりやすいな。と思ったので作りました。
同じように使いたい人は使ってみて頂ければと思います。
スクリプト本文と使い方
本文
#LLCコンバータの入出力電圧関係を計算して表示するスクリプトです。
#import
import math
import numpy as np
from matplotlib import pyplot as plt
#設定値
Vin=200;#入力電圧[V]
Vout=12;#出力電力[V]
fr=50*10**3;#共振周波数[Hz]
W=100;#負荷電力最大値[W]
S=5;#Lm/Lr
N=10;#巻き線比N1/N2
#定数の設定
Lm=1e-3;#励磁インダクタンス[H]
Lr=Lm/S;#漏れインダクタンス[H]
Cr=1/(Lr*(2*math.pi*fr)**2)#共振コンデンサ容量値[F]
[Lm/10**(-6),Lr/10**(-6),Cr/10**(-9)]#値の確認
#励磁インダクタンス[uH]漏れインダクタンス[uH]共振コンデンサ容量値[nF]
#出力電圧の計算
fsw_list=np.arange(1*10**3,60*10**3,100);#スイッチング周波数。1kHz->60kHzまで100Hz毎を振る。
F=fsw_list/fr;#fsw/fr
RL=Vout/(W/Vout);#負荷抵抗
RL_d=8/math.pi*N**2*RL;#1次側に換算した負荷抵抗
Q=np.sqrt(Lr/Cr)/RL_d;
Vout=1/np.sqrt((1+1/S-1/(S*F**2))**2 + (Q**2)*(F-1/F)**2) * 1/2 * Vin * 1/N;
#出力電圧vsスイッチング周波数の表示
plt.plot(fsw_list,Vout)
plt.xlabel("fsw[Hz]")
plt.ylabel("Vout[V]")
plt.grid()使い方
やっていることは使用条件を設定して、fswの値を振りながら以下の式を解いて、その結果をグラフにしているという単純な作業です。
$$\small{
V_{out}=\frac{1}{2}V_{in}\frac{1}{\sqrt{\left(1+\frac{1}{S}-\frac{1}{SF^2}\right)^2+Q^2\left(F-\frac{1}{F}\right)^2}}
\\
S=\frac{L_m}{L_r},F=\frac{f}{f_r},f_r=\frac{1}{2\pi\sqrt{L_rC_r}},Q=\frac{\sqrt{\frac{L_r}{C_r}}}{R_L’},R_L’=\frac{8}{\pi^2}\left(\frac{N_1}{N_2}\right)R_L
}$$
Vout:出力電圧[V], Vin:入力電圧[V], Lm:励磁インダクタンス[H], Lr:漏れインダクタンス[H],Cr:共振コンデンサ[F], f:スイッチング周波数[Hz], fr:Lr&Cr共振周波数[Hz], N1:1次巻き線, N2:2次巻き線, RL:負荷抵抗[Ω]
このスクリプトを使う人が実際にやること↓
- 「#設定値」で使用条件(Vin,Voutなど)を入力
- 「#定数の設定」で励磁インダクタンスを適当に入力
- 「#出力電圧の計算」でfsw_list変数に計算するスイッチング周波数の範囲を設定
そうすると「出力電圧vsスイッチング周波数」のグラフが表示されます。
jupyter notebookに書き込んで、定数を変えてグラフを見て、定数を変えて、、を繰り返して使うイメージです。
実行結果
上記のスクリプトで「#設定値」、「#定数の設定」、「#出力電圧の計算」に既に値を記入している条件でスクリプトを実行した結果を示します。
| 項目 | 値 |
|---|---|
| 入力電圧 | 200V |
| 出力電圧 | 12V |
| 共振周波数 | 50kHz |
| 負荷電力 | 100W |
| Lm/Lr | 5 |
| 巻き線比N1/N2 | 10 |
| 励磁インダクタンス | 1mH |
実行結果が以下です↓。
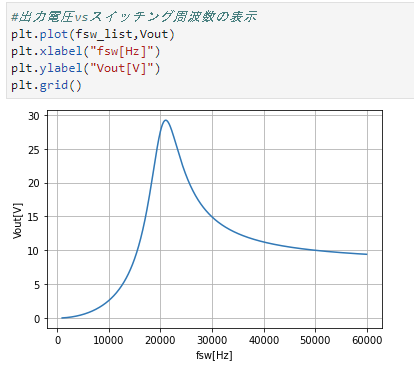
fr=50kHzに200*1/2*N2/N1の10Vが出ており、狙った通りの計算が出来ています。
今回はこれで終わります。最後までお読みいただきありがとうございました!