本記事はLLCコンバータの勉強をしてみよう。という記事の第1回目です。
1回目:【電源回路】LLCコンバータの動作原理(本記事)
2回目:【電源回路】LLCコンバータはなぜソフトスイッチングするのか?
3回目:【電源回路】LLCコンバータの出力電圧を計算するpythonスクリプト
4回目:【電源回路】LLCコンバータの設計手順①(パワーラインの設計編)
5回目:【電源回路】LLCコンバータを周波数可変に修正する
6回目:【電源回路】LLCコンバータの周波数特性を調べる
7回目:【電源回路】LLCコンバータの設計手順②(制御設計編)
8回目:【LLCコンバータ】インターリーブ運転のリップル低減効果を確認する
9回目:【LLCコンバータ】出力電圧Gvf(s)の周波数特性の負荷依存性を調べる
10回目:【LLCコンバータ】マルチレベル方式LLCコンバータの動作原理
11回目:【LLCコンバータ】LLCコンバータの双方向動作について
12回目:【双方向LLCコンバータ】双方向で電圧調整可能なCLLCコンバータについて解説
13回目:【CLLCコンバータ】LLCとCLLCでは、なぜ出力電圧VSスイッチング周波数の特性が違うのか?
今まで非共振コンバータをやってきて「俺はパワエレを理解したぜ!」という人を「おれ、何にもわかってないじゃん。。。」と絶望の谷に突き落とすコンバータです。
- LLCコンバータの動作原理
- 出力電圧がどのように求まるのか?
- シミュレーションで出力電圧を求めてみる!
というのをやってみます。誰かの参考になれば幸いです。では始めます。
まずは回路図
LLCコンバータはこんなのです。最も教科書に良く載ってるハーフブリッジ型で話を進めます。
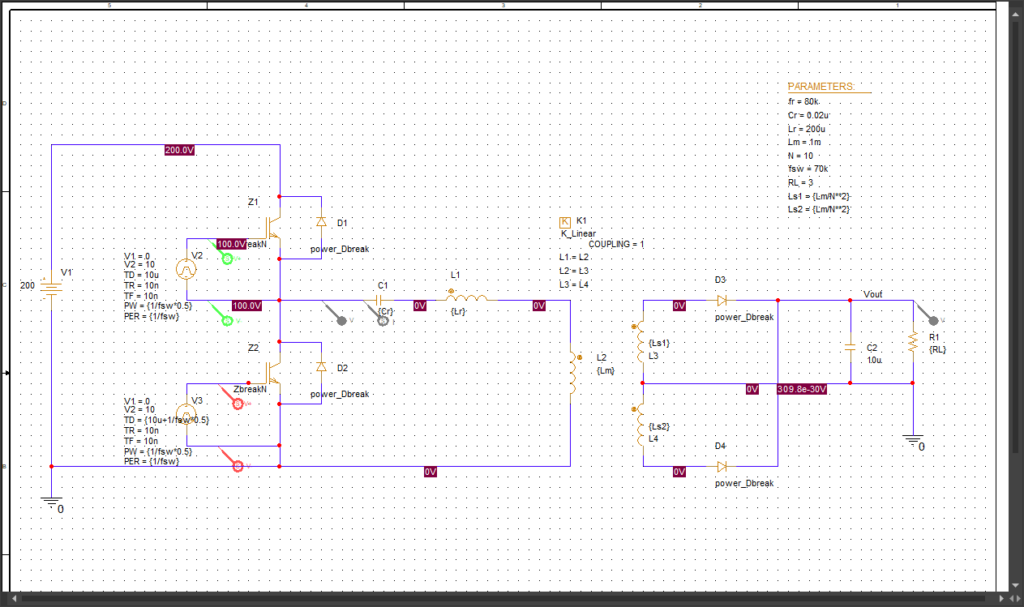
Z1,Z2を交互にON/OFFしてVoutに電力を送ってあげます。
Crが共振用コンデンサ、Lrが漏れインダクタンス、Lmが励磁インダクタンスです。トランスの漏れインダクタンスを利用して回路動作をさせているっていうのが特徴です。
動きを超ざっくり言うと
- Z1,Z2でON/OFFして、Cr,Lr,Lmに矩形波電圧を入力する。
- CとLで正弦波(sin波形)状の電流が流れる。
- その電流が二次側に伝えられる。
って感じです。
LLCコンバータはDUTY制御ではなくて、周波数制御
非共振コンバータをやっていた人は「コンバータはDutyを制御して出力電圧or電流を一定にしている。」と理解しているかと思いますが、共振型コンバータはDutyを固定して動かします。
LLCコンバータはDuty=50%固定でスイッチング周波数を制御して出力電圧or電流を一定にしています。
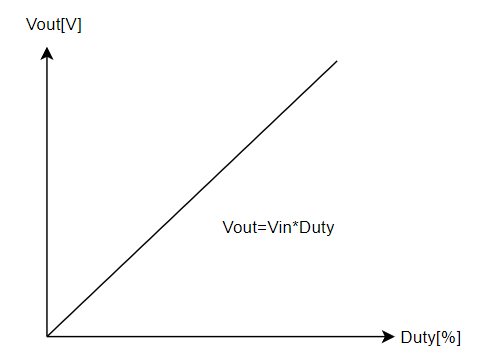
例えば非共振降圧コンバータだと、出力電圧の特性はこう↓Dutyによって決まりますが、
LLCコンバータだと出力電圧特性はこう↓スイッチング周波数fswによって決まります。
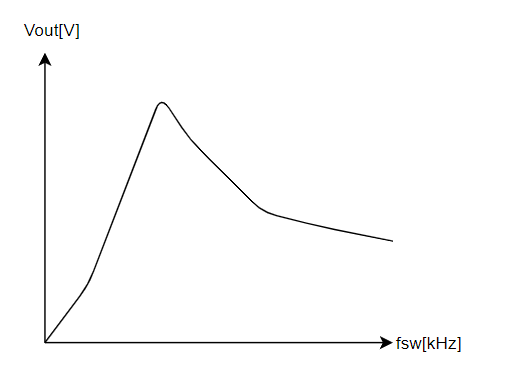
なので、入出力電圧関係式もfswが入ってきますし、制御ループの設計のときに考える伝達関数もΔDutyによるVoutの変化量Gdvではなくて、ΔfswによるVoutの変化量Gfvを考えます。
動作原理の解説
LLCコンバータは1~4までのモードがあります。
モード1:H-sideスイッチ=ON。Cr,Lrの共振で負荷電流が流れる。
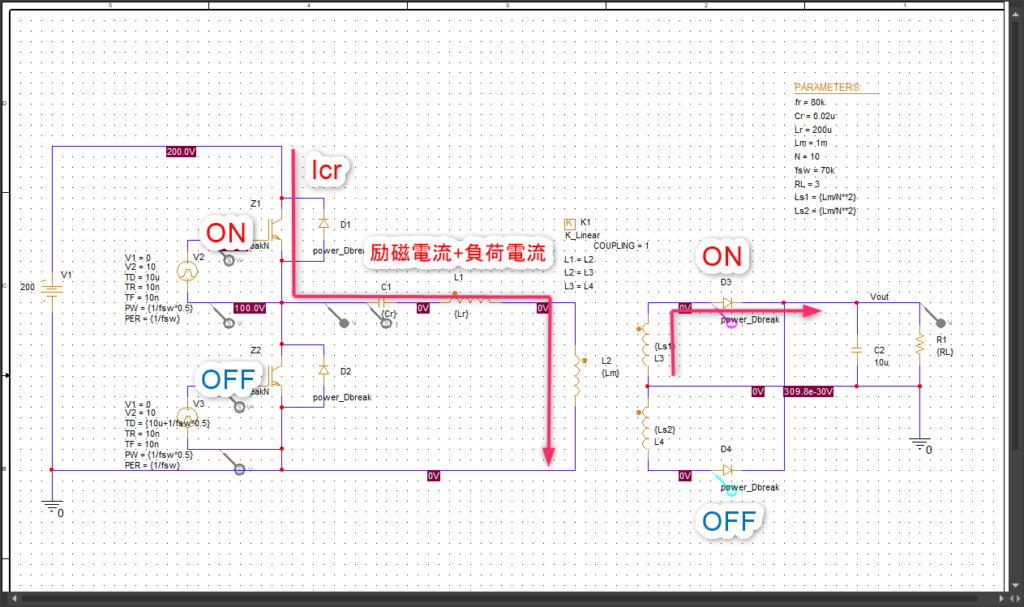
H-sideスイッチがONして共振回路に電流ICrが流れます。二次側にはD3がONして負荷電流が流れます。この負荷電流を1次側に換算した電流がCrとLrの周波数で共振し、励磁電流はCr,Lr,Lmの周波数で共振します。

二次側の負荷電流が0Aになったら、1次側のCr,Lr共振電流も無くなり、励磁電流だけになります。
そうなるとモード2になります。
モード2:Cr,Lrの共振電流終了
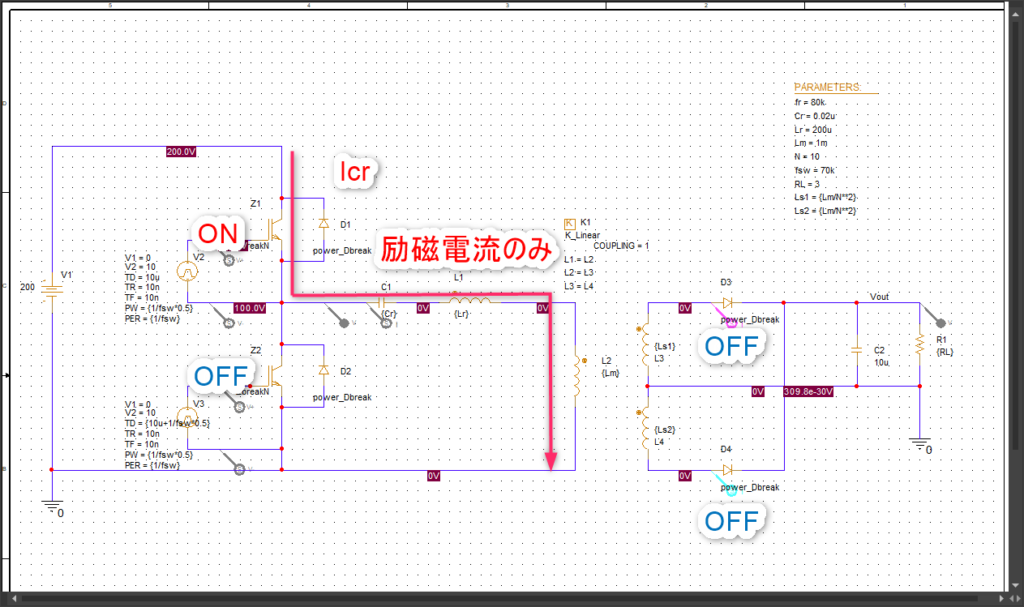
1次側は励磁電流のみになった状態がモード2です。ICrはCr,Lr,Lmで決まる周波数で共振した電流が流れます。
2次側はダイオードは両方OFFしている状態です。

Cr,Lrの共振周波数とCr,Lr,Lmの共振周波数が異なるので、共振電流Icrがfr->fmに代わってぐちゃっとなっています。
L-sideスイッチがONしてモード3へ移行します。
モード3:L-sideスイッチ=ON。Cr,Lrの共振電流が流れる。
あとはモード1の逆バージョンです。
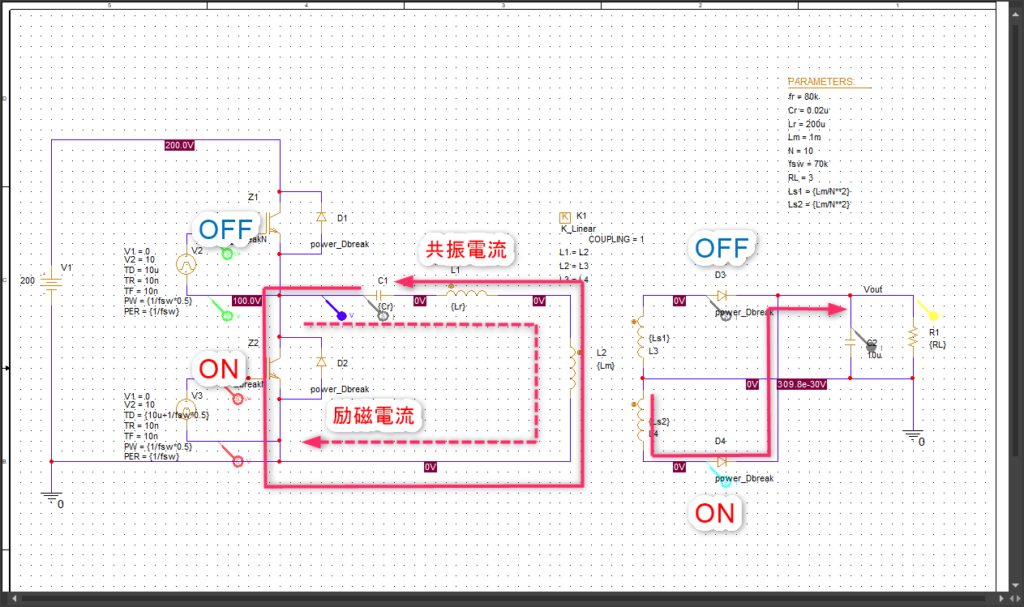
L-sideスイッチがONして共振電流がさきほどとは逆方向に流れます。それに伴い、2次側はD4がONし負荷電流が流れます。
2次側のインダクタには出力電圧Voutが負電圧方向にかかりますので、その巻き線比分の電圧が1次側の励磁インダクタンスにかかります。
その結果1次側の励磁電流は正の方向に流れつつもゆっくりと電流が低下していきます。

モード1と同様に負荷電流が0Aとなったら、モード4へ移行します。
モード4:Cr,Lrの共振電流終了
モード2と同様で励磁電流のみが流れている状態です。
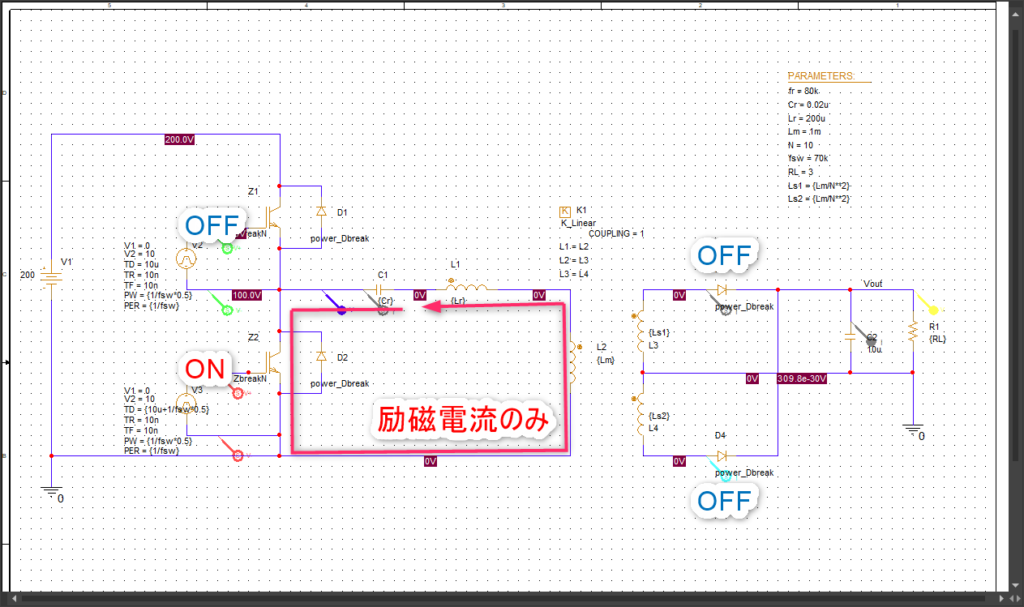
1次側は励磁電流のみになった状態がモード2です。ICrはCr,Lr,Lmで決まる周波数で共振した電流が流れます。
負荷電流が流れていないので、2次側はダイオードは両方OFFしている状態です。

H-sideスイッチがONしてモード1へ戻ります。
以上がLLCコンバータの動作の解説です。
次に出力電圧がどうやって計算されるか?を説明します。
入出力電圧関係式
出力電圧は以下の式で計算されます。
$$\small{
V_{out}=\frac{1}{2}V_{in}\frac{1}{\sqrt{\left(1+\frac{1}{S}-\frac{1}{SF^2}\right)^2+Q^2\left(F-\frac{1}{F}\right)^2}}
\\
S=\frac{L_m}{L_r},F=\frac{f}{f_r},f_r=\frac{1}{2\pi\sqrt{L_rC_r}},Q=\frac{\sqrt{\frac{L_r}{C_r}}}{R_L’},R_L’=\frac{8}{\pi^2}\left(\frac{N_1}{N_2}\right)R_L
}$$
Vout:出力電圧[V], Vin:入力電圧[V], Lm:励磁インダクタンス[H], Lr:漏れインダクタンス[H],Cr:共振コンデンサ[F], f:スイッチング周波数[Hz], fr:Lr&Cr共振周波数[Hz], N1:1次巻き線, N2:2次巻き線, RL:負荷抵抗[Ω]
意味わからん過ぎてイラついてきますね。
LLCコンバータで検索をするとよく出てきます。この式のfが変数です。fはスイッチング周波数のことで、このfの値を振ることにより、出力電圧を制御します。
これまでやってきた非共振コンバータのDutyの代わりみたいなイメージです。
この式でVout VS fswのグラフを描くと以下のようになります。

は?これが出力電圧特性???どうやって出力電圧制御するの?って感じですが、こんな感じ↓にfm~frの間でスイッチング周波数を移動させて出力電圧を制御します。
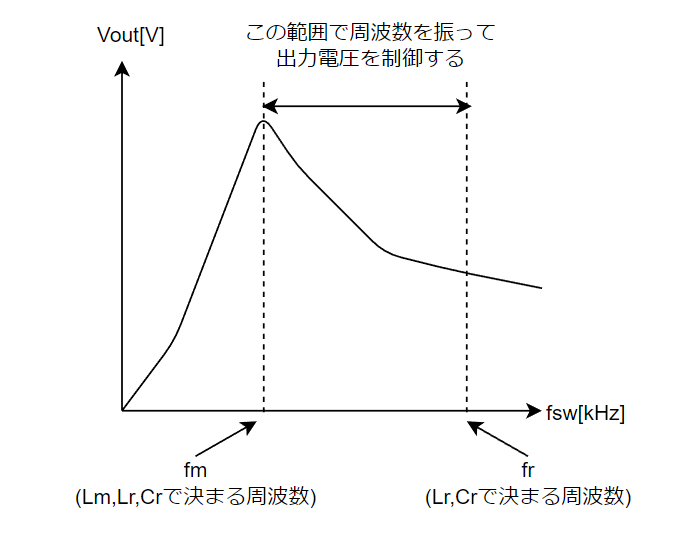
しかし、この式はあくまでも近似計算式です。fr付近では大体合うのですが、fmに近づくにつれて計算が狂ってきます。
なので、実使用上はfmのもうちょっと右の領域~frまでで使うイメージです。
ちなみにこの式がどうやって出てくるのか?はここを見ると詳しく書いてあります。
私もちゃんとは理解できていませんが、スイッチが交互にON/OFFして作る矩形波を正弦波に近似することによって、計算しやすくして出力電圧を解いているみたいなイメージです。
まぁ偉い人たちが解いた式なので、正しさは証明されているはずです。凡人はありがたく使わして頂きましょう。
シミュレーションで動作確認
めんどくさい理屈はこの辺にして、とりあえず動かしてみましょう。まずは最初にお見せした回路図です。(上で示した波形はこの回路でfsw=70kHzでシミュレーションした結果の波形です。)

この回路の各パラメータは以下の通りです。
| パラメータ | 値 | 単位 |
|---|---|---|
| 入力電圧 Vin | 200 | V |
| 共振コンデンサ Cr | 0.02 | uF |
| 漏れインダクタンス Lr | 200 | uH |
| 励磁インダクタンス Lm | 1 | mH |
| 巻き線比 N=n1/n2 | 10 | – |
| 負荷抵抗 RL | 3 | Ω |
上で記載した出力電圧の式を使ってグラフを描くと以下のようになります。
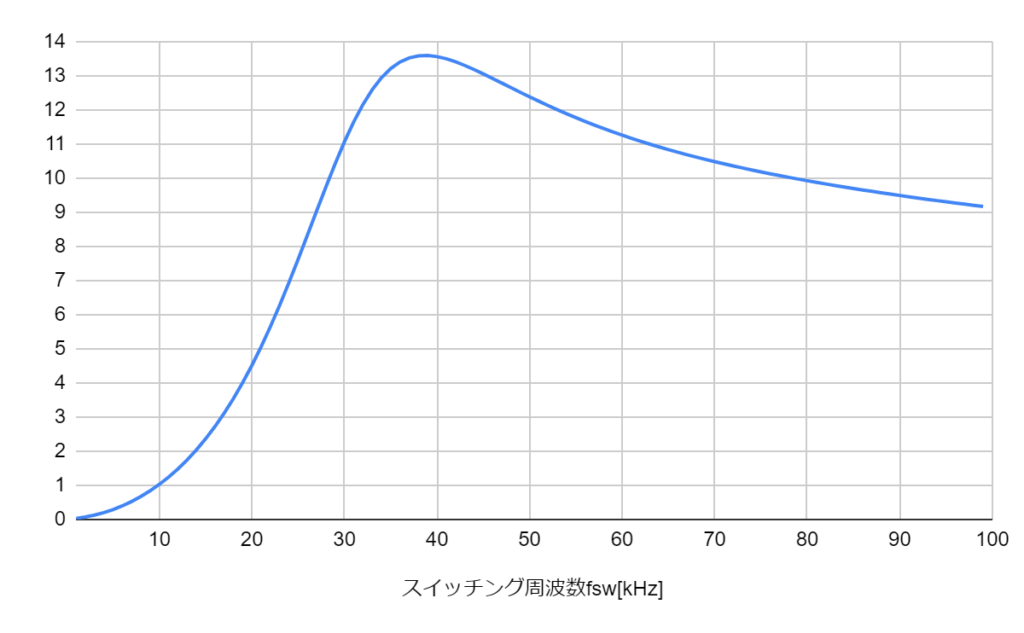
共振周波数fr=80kHz付近で出力電圧10Vくらい。
励磁インダクタンスを含めた共振周波数fm=38kHz付近。
と読み取れます。
ではシミュレーションでスイッチング周波数を1kHz~80kHzまで振って、出力電圧vsスイッチング周波数のグラフを描いてみましょう。
シミュレーション結果の出力電圧波形が以下です。
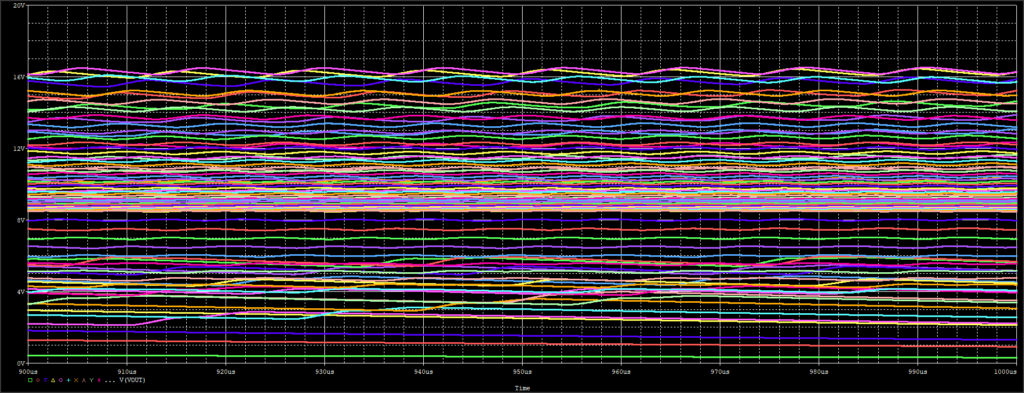
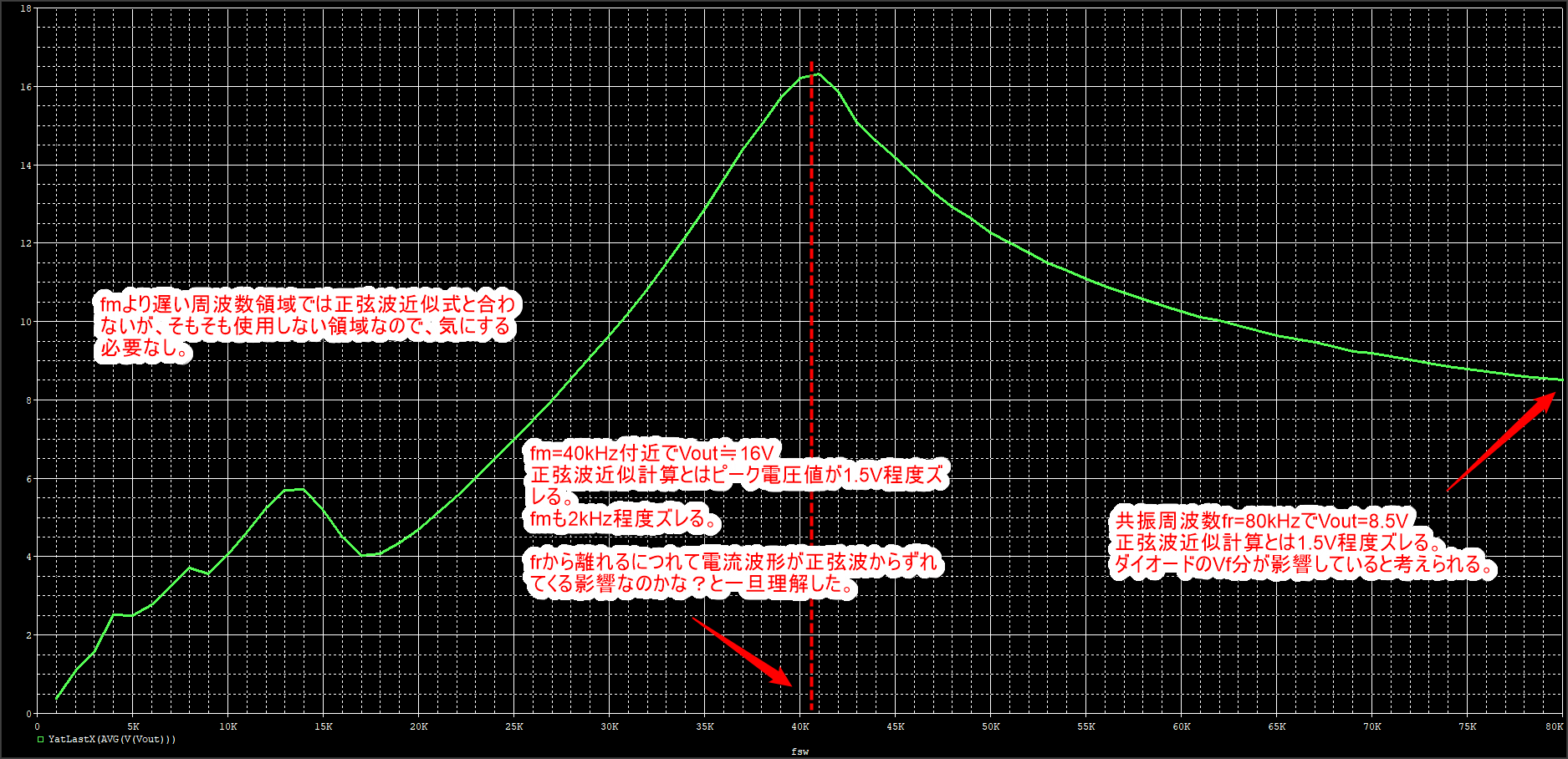
これじゃわけがわからないので、それぞれ平均を取って横軸fsw、縦軸Voutのグラフに書き直しました↓。
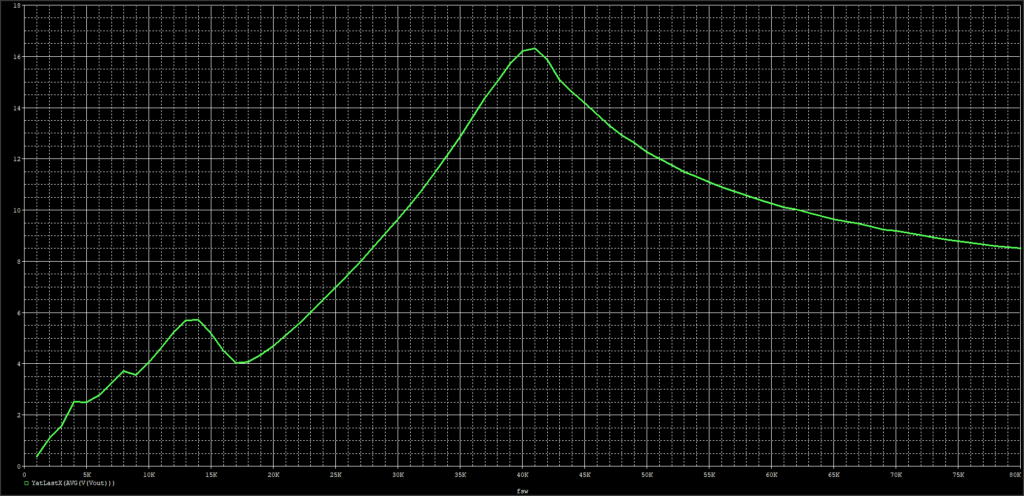
これを見るとびみょーに近似式に比べるとピーク周波数が高域に来て、ピーク電圧がよりとがっています。
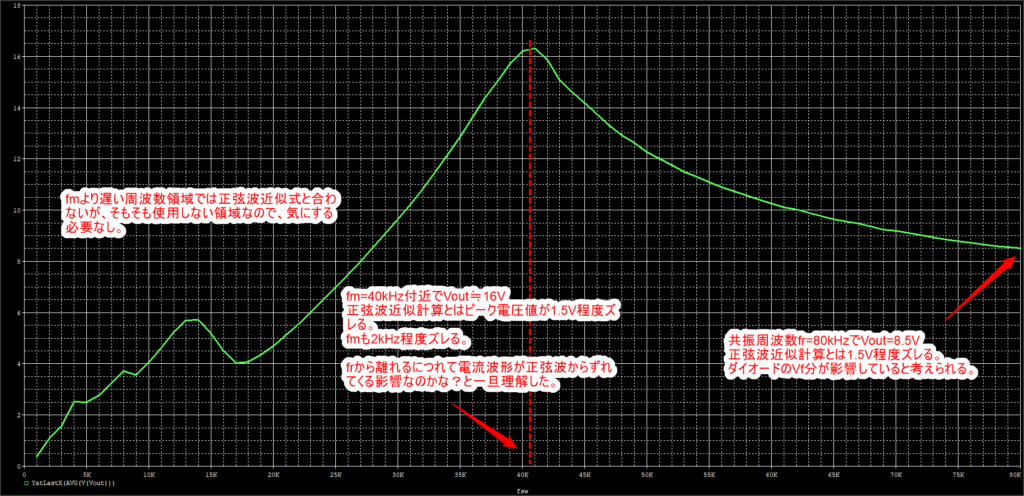
詳細は理解していませんが、、、frから離れれば離れる程、正弦波からずれていくので近似式と合わなくなっていくのだろうと理解しました。
なので、近似式を目安にしつつ、最終的にはシミュレーションで確認。というのが必要になるって感じですね。
一旦出力電圧特性まで見れたので、今回はこんなところで終わりにします。
いや~共振コンバータは難しいっすねぇ。最後までお読みいただきありがとうございました。