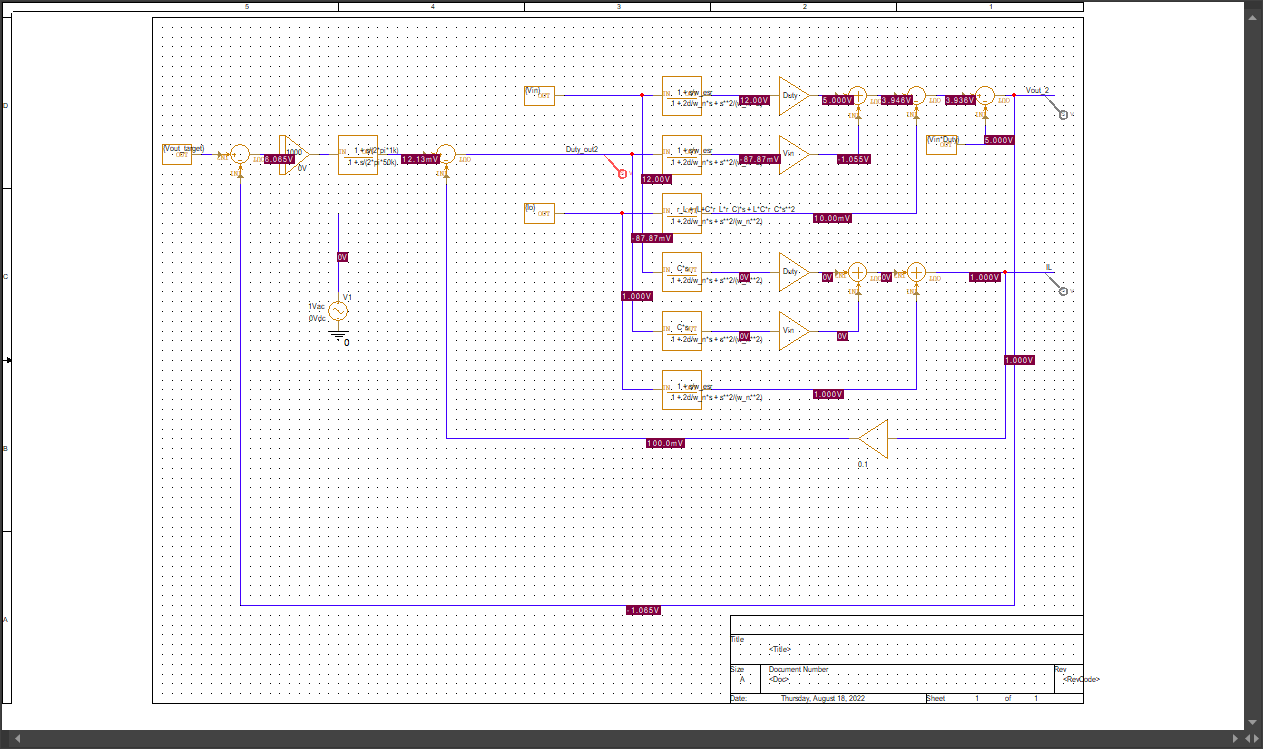
前々回記事で状態平均化法を使って非絶縁型降圧スイッチングレギュレータの伝達関数を導出しました。前回記事ではその結果を用いて電圧モード制御の動作モデルをPspice for TIで作りました。
今回は更に電流モード制御の動作モデルをPspice for TIで作りましたので、その内容を報告します。
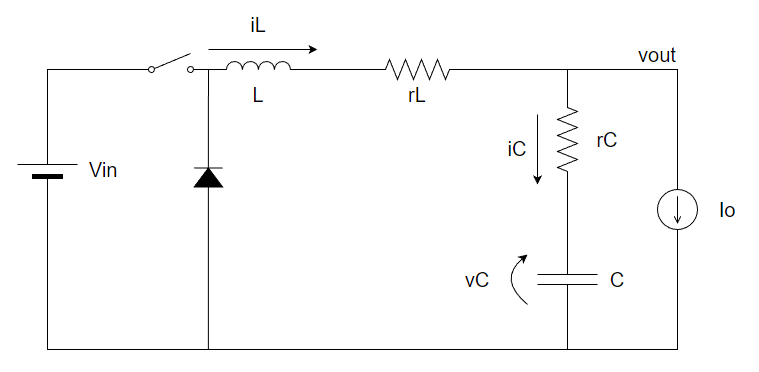
- 降圧スイッチングレギュレータの伝達関数
- 電流モード制御の動作モデルの作り方
誰かの参考になれば幸いです。では、やってみます。
前々回記事の結論
非絶縁型降圧スイッチングレギュレータの伝達関数は以下の通りになります。
出力電圧に関する伝達関数は以下の通り
$$\small{\frac{ΔVout(s)}{ΔVin}=G_{vv}=\frac{1}{P(s)} \left( 1+\frac{s}{ω_{esr}} \right) Duty}$$
$$\small{\frac{ΔVout(s)}{ΔDuty}=G_{dv}=\frac{1}{P(s)} \left( 1+\frac{s}{ω_{esr}} \right) Vin}$$
$$\small{\frac{ΔVout(s)}{ΔIo}=G_{iv}=-\frac{1}{P(s)} \left( s^2LCr_C+s(L+Cr_Lr_C)+r_L \right)}$$
出力コイル電流に関する伝達関数は以下の通り
$$\small{\frac{ΔIL(s)}{ΔVin}=G_{vi}=\frac{C*Duty*s}{P(s)}}$$
$$\small{\frac{ΔIL(s)}{ΔIo}=G_{ii}=\frac{\frac{s}{ω_{esr}}+1}{P(s)}}$$
$$\small{\frac{ΔIL(s)}{ΔDuty}=G_{di}=\frac{C*Vin*s}{P(s)}}$$
ただし
$$\small{P(s)=\frac{s^2}{ω_n^2}+\frac{2δ}{ω_n}s+1}$$
$$\small{ω_n=\frac{1}{\sqrt{LC}},δ=\frac{r_L+r_C}{2}\sqrt{\frac{C}{L}},ωesr=\frac{1}{Cr_C}}$$
定常解(静特性)
$$\small{V_{out}=DutyVin-I_or_L}$$
$$\small{I_L=Io}$$
Vin:入力電圧[V]、Vout:出力電圧[V]、Duty:スイッチングON DUTY[%]、L:出力コイルインダクタンス値[H]、C:出力コンデンサ容量値[F]、r_L:インダクタのDCR[Ω]、r_C:コンデンサのESR[Ω]、Io:出力電流[A]、IL:出力コイル電流[A]
導出過程の詳細は前々回記事を参照してください。
Pspice for TIには伝達関数を表現する”LAPLACE”があるので、それを使って動作モデルを作ります。
電流モード制御なのでILもフィードバックします。
作成した動作モデル
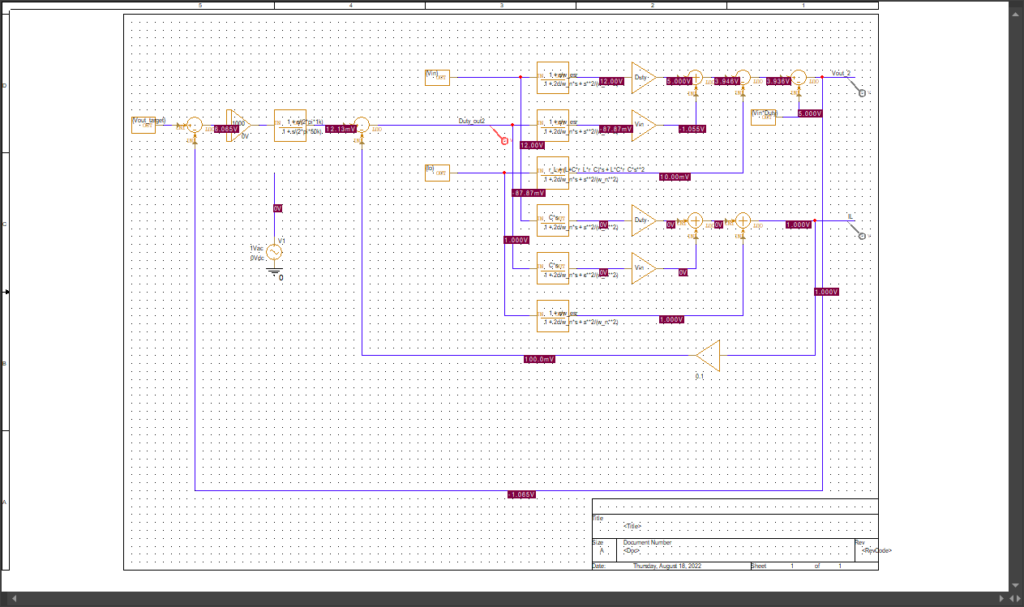
出力電圧部
まず出力電圧部分は以下のようにしました。最初に書いた出力電圧に関する伝達関数を全て足し合わせた形です。
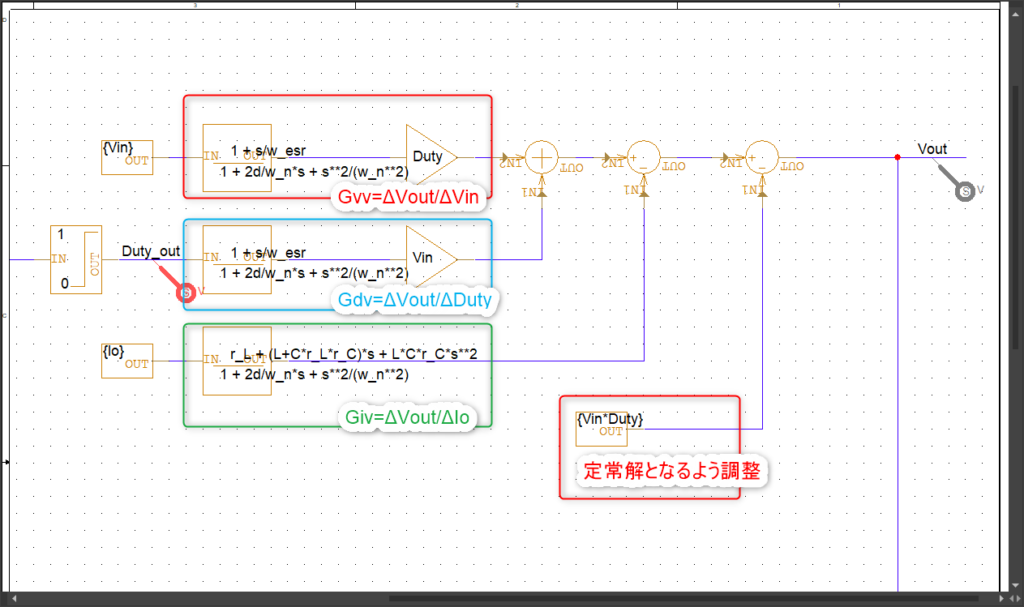
Vin,Duty,Ioの変動による出力電圧の変動は以下の通り足し算になります。足すことで変動分を計算しています。(ΔIoに関しては符号が逆になるので注意です。)
$$\scriptsize{ΔVout(s)=\frac{1}{P(s)} \left( \left(1+\frac{s}{ω_{esr}} \right)DutyΔVin
+\left(1+\frac{s}{ω_{esr}} \right)VinΔDuty
-\left(s^2LCr_C+s(L+Cr_Lr_C)+r_L\right)ΔIo \right)}$$
それから定常解(静特性)を引き算しています。これはs=0を入れたときのそれぞれの出力を見たらわかるかと思うんですが、
$$\small{Gvv(s=0)=Vin*Duty, Gdv(s=0)=Vin*Duty, Giv(s=0)=r_L*Io\\
Vout(s=0)=Gvv+Gdv-Giv\\=Vin*Duty+Vin*Duty-r_L*Io\\=2Vin*Duty-r_L*Io}$$
とVoutが定常解Vin*Duty-r_L*Ioに比べてVin*Duty分だけ大きくなります。そのためVin*Duty分引き算して調整してあげてます。
出力コイル電流部
次に出力コイル電流部分は以下のようにしました。最初に書いた出力電圧に関する伝達関数を全て足し合わせた形です。
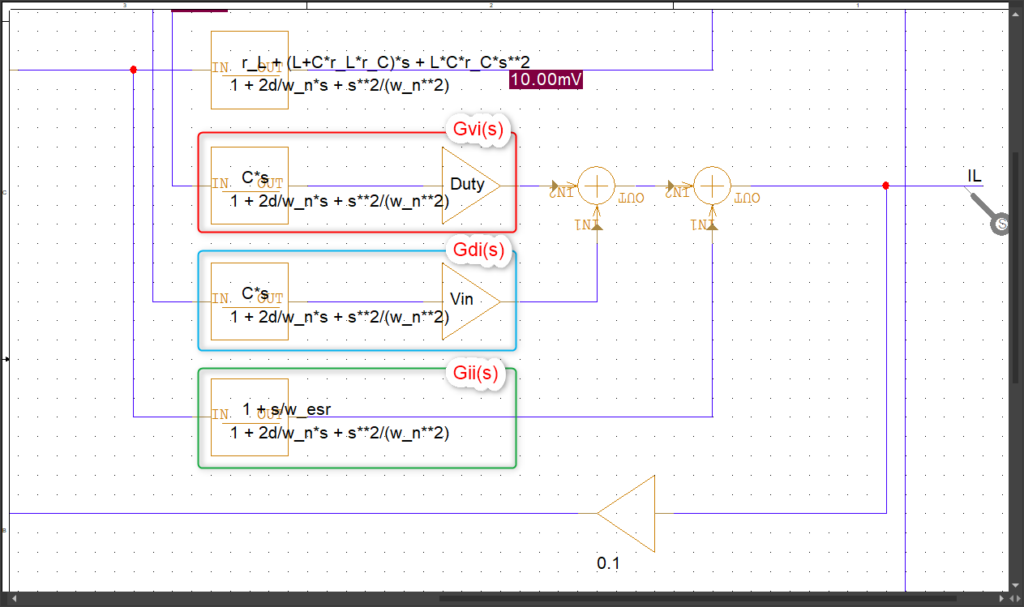
Vin,Duty,Ioの変動による出力電圧の変動は以下の通り足し算になります。
$$\small{
Δi_L=\frac{1}{P(s)}\left(
CDutysΔVin
+\left(\frac{s}{ω_{esr}}+1\right)ΔIo
+CVinsΔDuty
\right)
}$$
電流フィードバック部
次に電流フィードバック部分です。
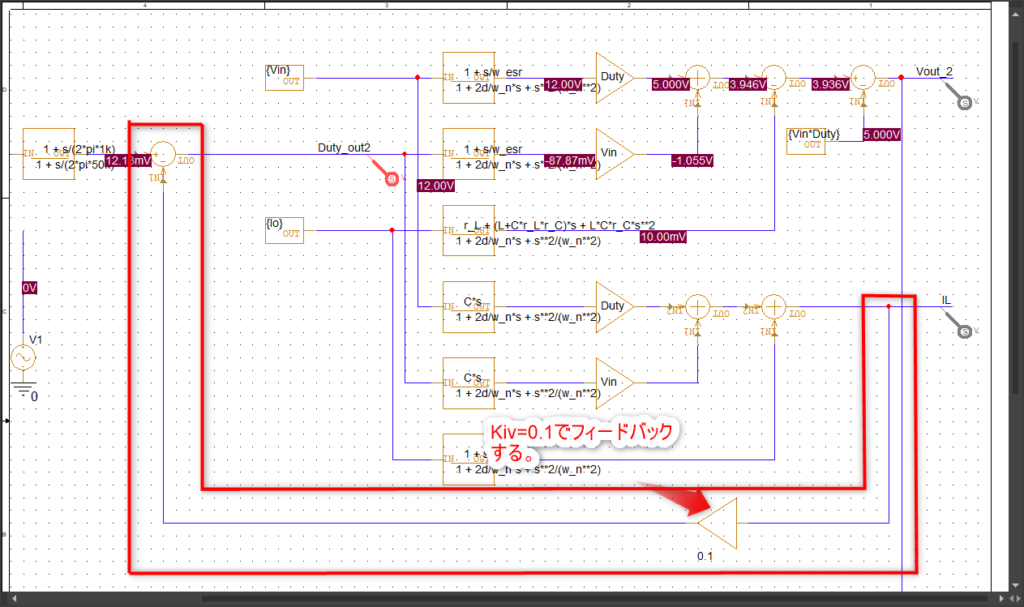
出力コイル電流をフィードバックしてます。帰還係数は適当に0.1としています。
電圧フィードバック部
次にフィードバック制御部です。
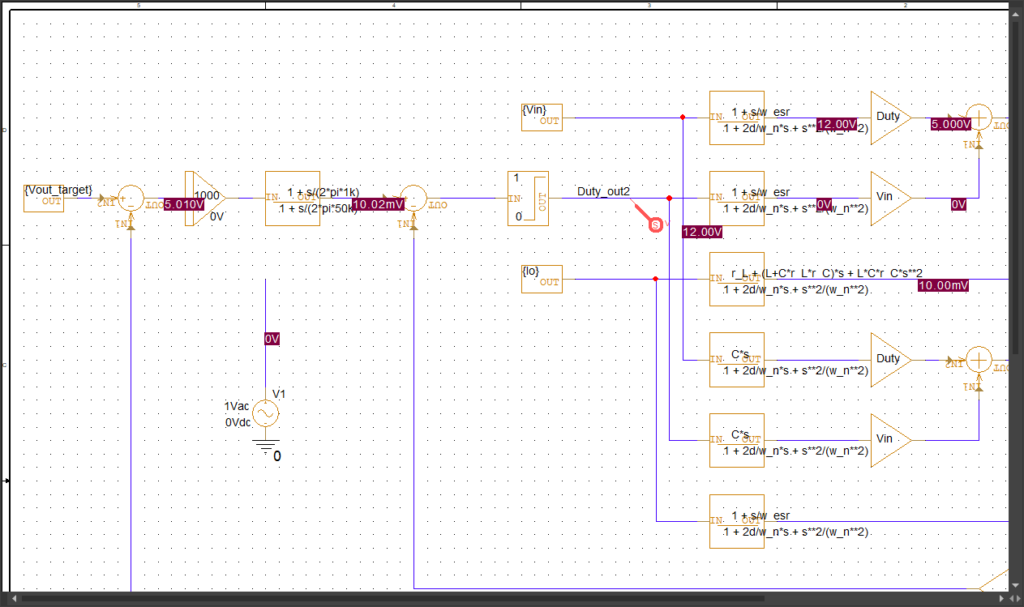
出力電圧の狙い値と比較して、Gc(s)のコントローラーでDutyを計算して、Limitで0~100%となるように制限を掛けてます。
Gc(s)は2pole1zero補償器を使用しています。(2個ポールがあって、1個ゼロがある。)電流モード制御を行っているので、この補償器を使用しています。
$$\small{
G_c(s)=\frac{A_o}{s}\frac{1+\frac{s}{2pif_{z1}}}{1+\frac{s}{2pif_{p1}}}
}$$
制御の係数は適当に設定しています。
DCゲインAoはとりあえず60dBくらい。
ゼロ点の設定には少し考えます。まず以下のプラント部分だけの伝達関数で周波数特性を調べます。
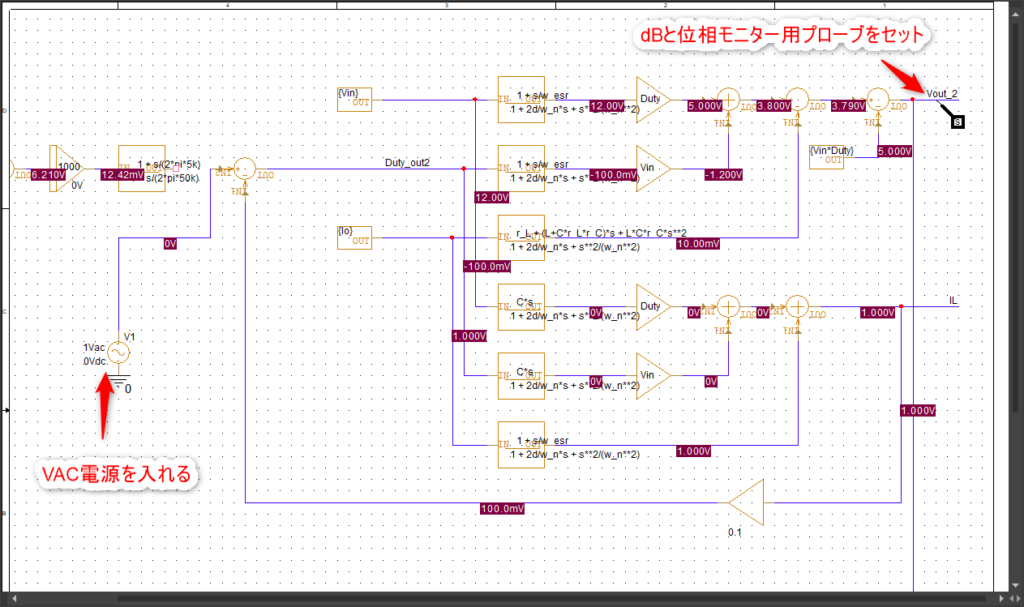
シミュレーション結果が以下の通りです。
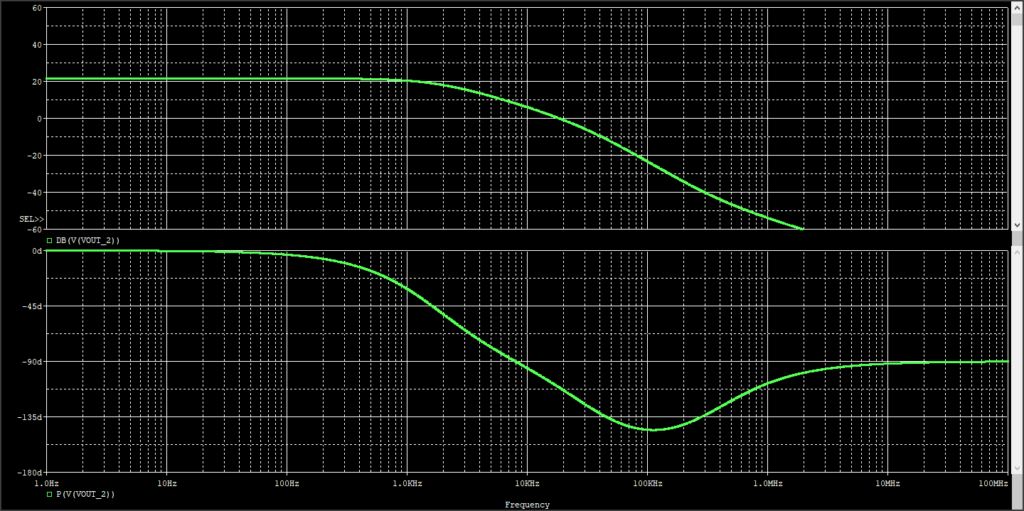
これを見ると1kHzくらいにポールがあり、それから20dB/decで落ちて行っているのが分かります。
これが電流モード制御のすごいところです。
電圧モード制御だとLCの2次ポールが出来てしまうのですが、それが電流モード制御ではコイル電流をフィードバックすることにより2次ポールが打ち消されて、1次ポールに見えます。
それによって制御設計が簡単になります。
電圧モード制御では2次ポールに2個のゼロ点をぶつけて打ち消されていましたが、
電流モード制御ではこの1kHzのところに1個のゼロ点をブチ当てれば、ポールを打ち消せます。
あとはAo/sの伝達関数でゲインが一直線に落ちていくように制御を設計できます。
とごちゃごちゃ言いましたが、制御的には1kHzのところにゼロ点を入れます。ということで以下のようにGc(s)を設定しました。
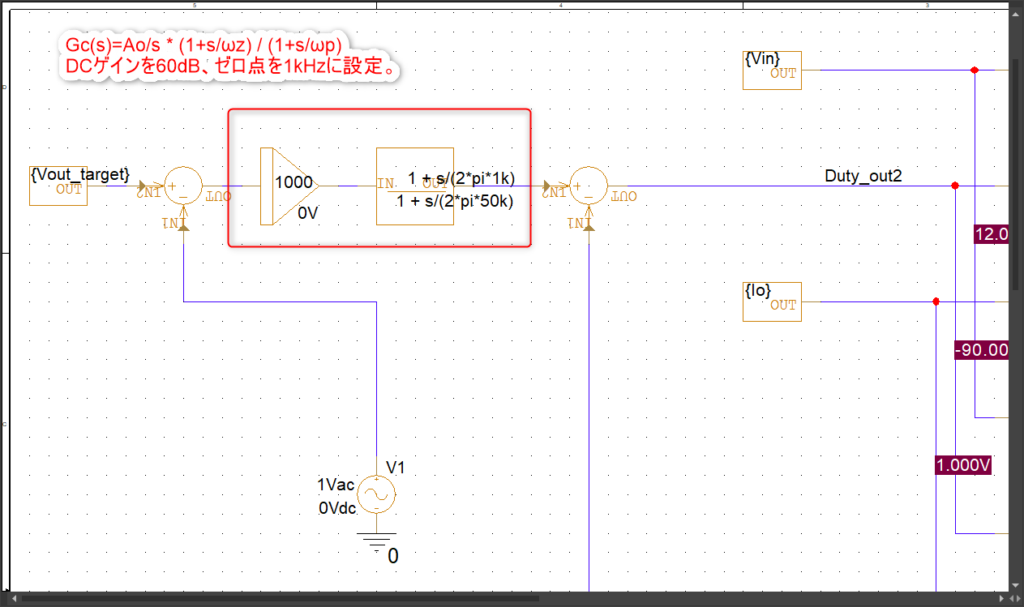
では、ちゃんと制御がイケてるかを確認してみます。回路を以下のように書き換えて
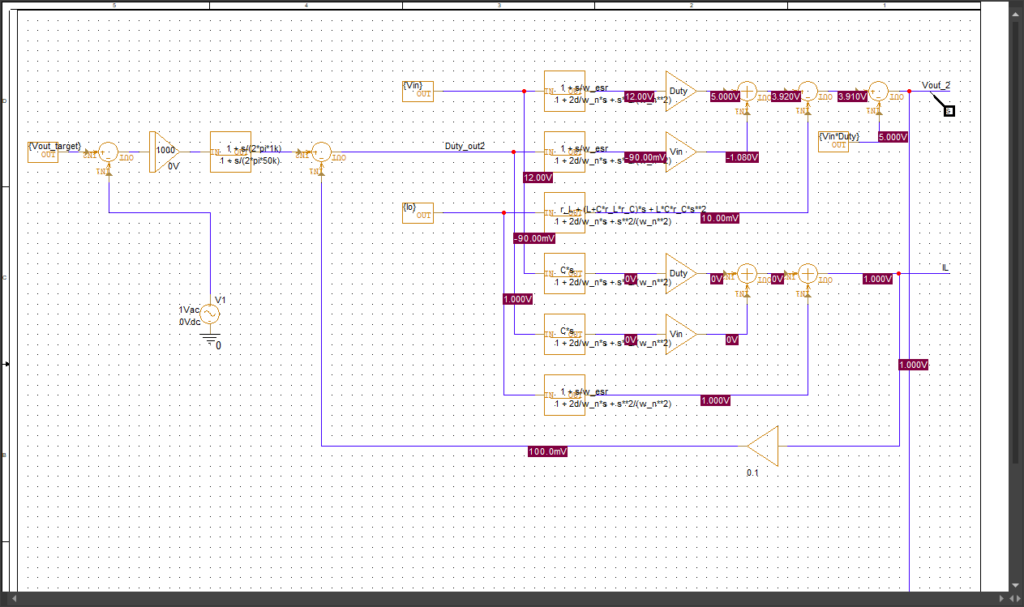
シミュレーション結果は以下の通り、ちゃんと1kHz付近のポールが打ち消されています。OKですね。位相余裕度も確保できており、OKOKです。
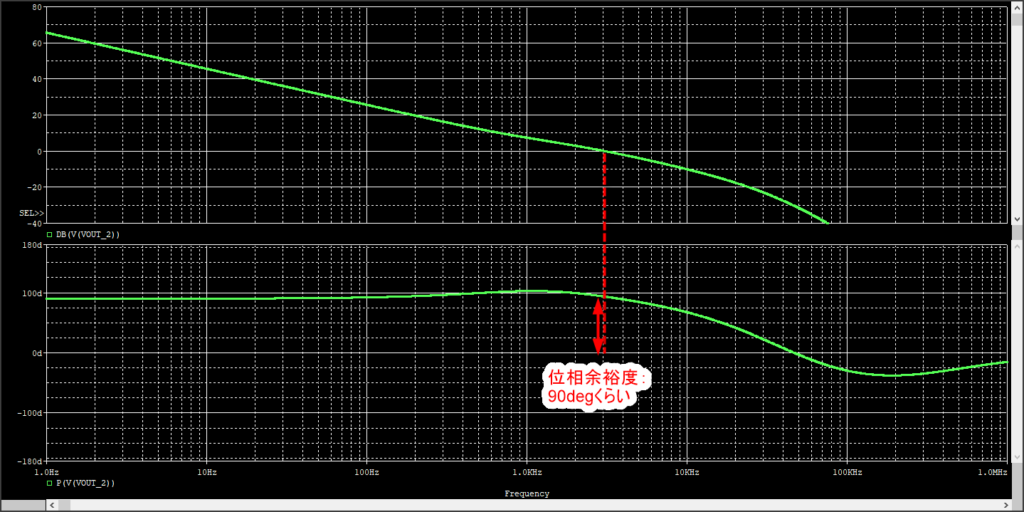
ポールはなんとなく50kHz。適当です。
最後にパラメータです。

パラメータを設定しています。Vout=5V狙いで、Vin=12V、伝達関数のδ、ωn、ωesrもここで計算しています。まぁそれだけです。
ざっくりですが、これを非絶縁型降圧スイッチングレギュレータ(電流モード制御)の動作モデルとしました。
シミュレーション結果
Vin電圧を6V~18Vまで変化しながら、t=2msの時間解析をしました。
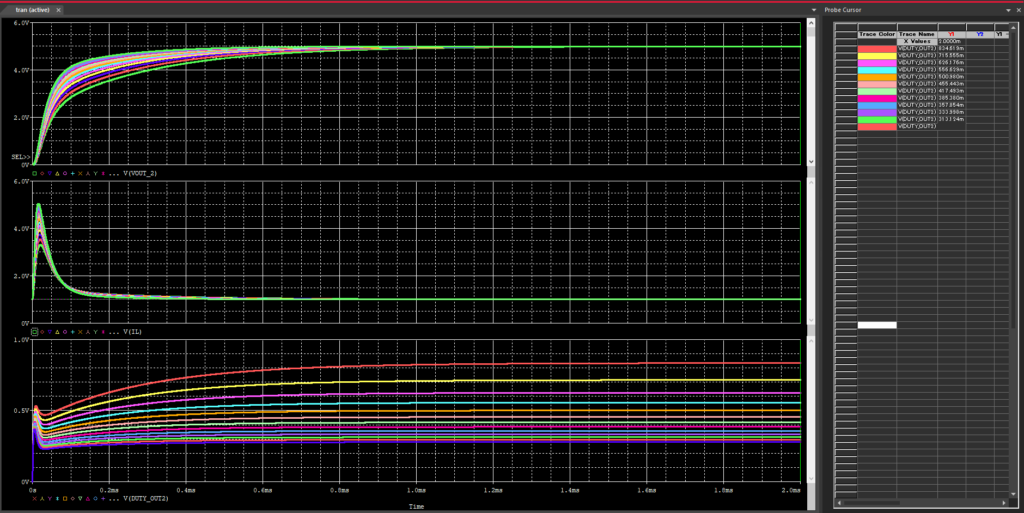
上:Vout
中:IL
下:Duty
t=0ms~1msに拡大しました。
Voutは全て狙い値の5Vに収束していて問題なしですね。
Dutyはいくつも波形が出てきていてわかりずらいので、収束しているポイントでいくつになっているかを表にしました↓。
| Vin[V] | Duty(sim値)[%] | Duty(想定値=Vout/Vin)[%] |
|---|---|---|
| 6 | 83.62 | 83.00 |
| 7 | 71.56 | 71.43 |
| 8 | 62.62 | 62.50 |
| 9 | 55.66 | 55.56 |
| 10 | 50.10 | 50.00 |
| 11 | 45.54 | 45.45 |
| 12 | 41.75 | 41.67 |
| 13 | 38.54 | 38.46 |
| 14 | 35.79 | 35.71 |
| 15 | 33.40 | 33.33 |
| 16 | 31.31 | 31.25 |
| 17 | 29.47 | 29.41 |
| 18 | 27.83 | 27.78 |
想定値Vout/Vinと比較するとほとんど変わりないです。問題なしかと。
まとめ
今回は非絶縁型降圧スイッチングレギュレータの動作モデルを作成しました。出力電圧と出力コイル電流をフィードバックしてDutyを制御する機能もモデル化しました(電流モード制御)。
スイッチングしている様をシミュレーションでやってもらおうとするとかなり時間がかかってしまいます。ざっくりシステム全体の動作を見たいんよ。という用途には有用かと思います。
よくわからないこと
この記事はシミュレーションしながら書いていたのですが、イケてない箇所がありました。
t=1secでシミュレーションすると同じような結果が得られません。
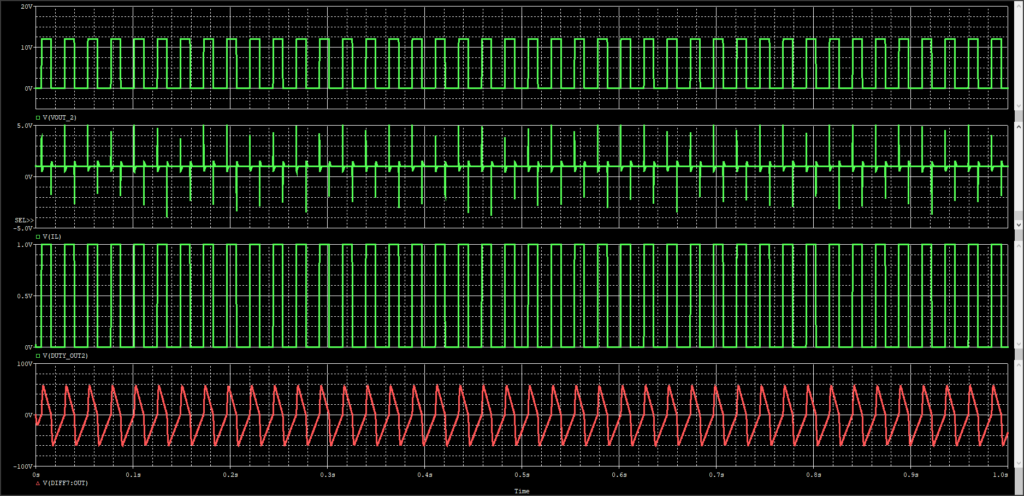
Vout
IL
Duty
limiterの手前
Dutyが0か100%に吹っ飛んでますね。発振してます。なんででしょうね。
予想としては何かシミュレーションのスタート地点が微妙に違うんですかね。t=1secのシミュレーションではスタートが微妙に遅くて、制御器の積分要素がグワーッと足し算しまくった状態でシミュレーションスタートしちゃって、ふっとんじゃってるっていうのがまぁ予想です。
フワフワした予想ですが、直ったら加筆します。解決しました↓。
ついでにむだ時間要素についても追加しました。
はい、とりあえず本記事は以上になります。誰かの参考になれば幸いです。最後までお読みいただきありがとうございました!!