皆さん、お疲れ様です。
LLCコンバータの設計に挑戦中のものです。
①仕様をとりあえず決めて、色々勉強して定数を設定してみた。→その記事はこちら
②その定数でLTspiceでシミュレーションしてみたが、挙動がおかしくて苦戦。とりあえず動いたがリップル電流がやたらでかい。→その記事はこちら
③仕様を見直した方がいいのかな?と思い始めた。定数を設定の計算をやるのがめんどくさ過ぎて計算シートを作った。→その記事はこちら
④ふわっとした感覚で仕様を緩和して定数を再設定した。→その記事はこちら
⑤自分の思うままにプラント伝達関数を導出してみた。→その記事はこちら
⑥プラント伝達関数をpythonでボード線図を描いてみた。→その記事はこちら
⑦その伝達関数についてグダグダ考察。→その記事はこちら
今のところプラント伝達関数をどう保証したらいいかよくわからん。
・伝達関数の分子にsがおるので、s=0(DC状態)ではGplant=0になる。
・DCゲインが0ということは20log|G|=-∞になる。
・-∞に何足しても-∞じゃん。
ということで自分で考えていてもしょうがないので、企業の資料から勉強します。
↓TI(Texas Instruments)の資料「Feedback Loop Design of an LLC Resonant Power Converter」
伝達関数をGm(s)とGc(s)に分けている
コントローラー部分を含めた構成は以下。(引用)

プラント部と電圧->周波数変換回路とパワーMOSのQ1,Q2を叩きに行く部分をひっくるめてGm(s)としている。
またコントローラー部分をGc(s)としている。
Gm(s)とは違ってGc(s)は解析的に表現できるよって書いてある。
じゃあGc(s)ってどんな伝達関数なの?
$$G_c(s)=\frac{\frac{s}{\frac{1}{R1*C1}}+1}{\frac{s}{ω_l}*(\frac{s}{ω_{p_opto}}+1)}$$
ちょっと変形して
$$G_c(s)=\frac{sR_1C_1+1}{\frac{s}{ω_l}*(\frac{s}{ω_{p_opto}}+1)}$$
これが何でこうなるんかって話。
まずオペアンプから
まずはオペアンプの部分だけ抜き出して考える。
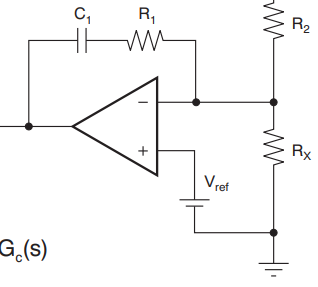
ここの伝達関数は以下のような式で表せます。
$$G_a(s)=\frac{R_1+\frac{1}{sC_1}}{R_2}$$
$$G_a(s)=\frac{1+sC_1R_1}{sC_1R_2}$$
なんでこうなるのかの導出過程は以下を参照してください。
最終形態の式2-6を見ましょう。

これのC1がないバージョンが検討しているものですね。回路図上でC1はないのでこの項をとっぱらったら先ほどの式がでます。
以上。粗い説明でした。
これでGc(s)の式の分子が出てきましたね。
次はフォトカプラのとこ
わからん。。。わからんけど、ポールがあるらしい。
いや~まぁわからないけど、こうなるんでしょ。(おい。)
どんなボード線図になるのか?
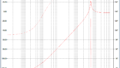
wlで計算されるDCゲインがあって、
分母にsがいるのでDCゲインから20dB/decで落ちて行って、
C1R1で計算されるゼロ点があるからバキッと上げて、
フォトカプラのポールから下げると。(大体2π*10kHzくらいらしい。)って書いてある。
イメージはこんな感じ。(きったねぇなぁ。。。)
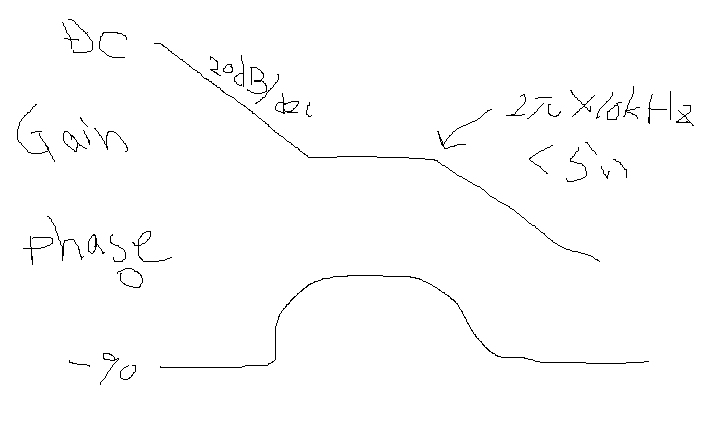
今日はGc(s)で終わりです。
次はGm(s)を見てみます。どうやら計算では求められなくて、測定によって求めるらしい。