みなさま、お疲れ様です。
本記事は非絶縁降圧スイッチングレギュレータの勉強をしてみよう。という記事の第9回目です。
1回目:【電源回路基礎】非絶縁降圧スイッチングレギュレータの動作原理
2回目:【電源回路基礎】MOSFETがどうやってONするかを知って欲しい
3回目:【電源回路基礎】非絶縁降圧スイッチングレギュレータの設計手順①(パワーライン編)
4回目:【電源回路基礎】非絶縁降圧スイッチングレギュレータの出力がなぜ一定になるのか?
5回目:【電源回路基礎】スイッチングレギュレータの安定、不安定とは?
6回目:【電源回路基礎】非絶縁降圧スイッチングレギュレータの制御方法(電圧モードと電流モード)
7回目:【制御工学】状態平均化法による非絶縁型降圧スイッチングレギュレータの伝達関数の導出
8回目:【制御工学】Type3補償器の超簡単な設計方法【実例あり】
9回目:【電源回路基礎】非絶縁降圧スイッチングレギュレータの設計手順(制御設計 ピーク電流モード制御編)(本記事)
今回はピーク電流モード制御の制御器設計を解説します。
ピーク電流モード制御にはPI補償器を使います。
ピーク電流モード制御の制御設計が分からない!!!
と悩まれている方の参考になれば幸いです。
結論:プラントの周波数特性をボード線図描いて、1次ポールにPIのゼロ点をブチ当てる
ピーク電流モード制御の制御設計は超簡単です。手順は以下の通りです。
- プラントの周波数特性を描く。(1次ポールになる。)
- プラントの極周波数と同じ周波数にPI制御器のゼロ点を配置する。
- DCゲインを調整して終わり。
前回記事で解説した電圧モード制御と比べると超簡単ですね。
でも初めての人からすると意味不明かもしれませんので、順番に解説します。
【おさらい】ピーク電流モード制御とは?
第6回記事で解説しましたが、非絶縁降圧スイッチングレギュレータには”電圧モード制御”と”電流モード制御”の二つがあります。
| 制御 | フィードバック | 特徴 |
|---|---|---|
| 電圧モード制御 | 出力電圧 | LCの2次のポールで位相が180°回転 |
| 電流モード制御 | 出力電圧+コイル電流 | LCの2次ポールが打ち消されて1次のポールになる |
電流モード制御では出力電圧とコイル電流をフィードバックします。
略回路図は以下の通りです。
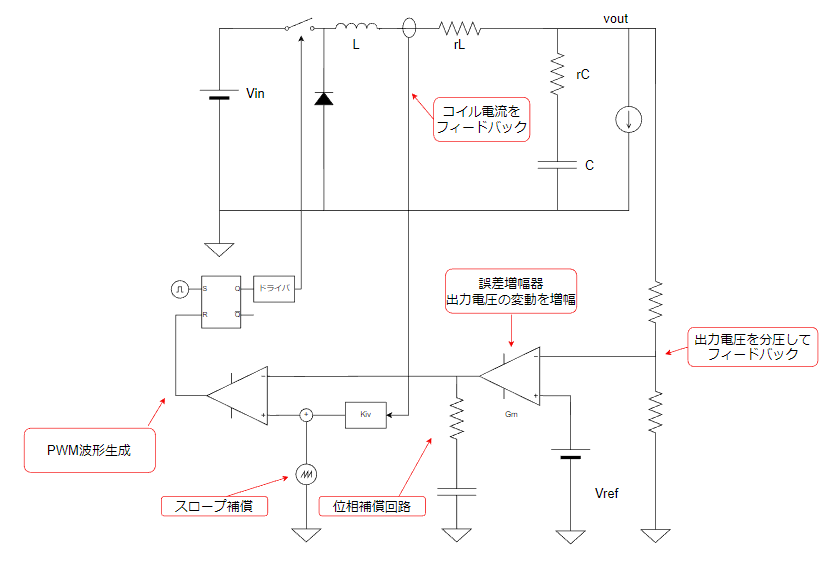
SLOPE補償はサブハーモニック発振防止のために必要です。
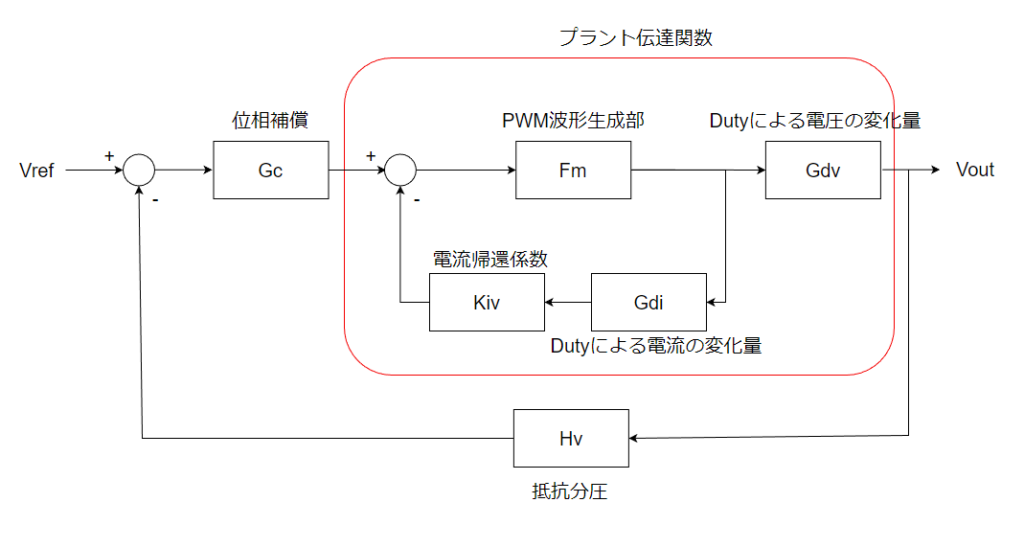
ブロック線図は以下のようになります。
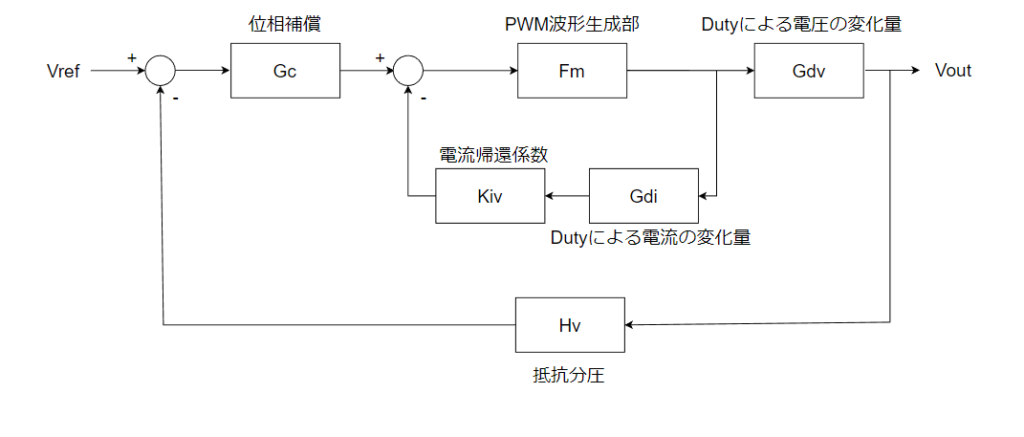
こうすることによって、出力LCフィルタの2次ポールが1次ポールになります。それで制御設計が楽になります。
プラント伝達関数は以下の通りです。
$$\small{\frac{ΔVout(s)}{ΔDuty}=G_{dv}=\frac{1}{P(s)} \left( 1+\frac{s}{ω_{esr}} \right) Vin}$$
$$\small{\frac{ΔIL(s)}{ΔDuty}=G_{di}=\frac{C*Vin*s}{P(s)}}$$
ただし
$$\small{P(s)=\frac{s^2}{ω_n^2}+\frac{2δ}{ω_n}s+1}$$
$$\small{ω_n=\frac{1}{\sqrt{LC}},δ=\frac{r_L+r_C}{2}\sqrt{\frac{C}{L}},ωesr=\frac{1}{Cr_C}}$$
Vin:入力電圧[V]、Vout:出力電圧[V]、Duty:スイッチングON DUTY[%]、L:出力コイルインダクタンス値[H]、C:出力コンデンサ容量値[F]、r_L:インダクタのDCR[Ω]、r_C:コンデンサのESR[Ω]、Io:出力電流[A]
$$\small{
Fm=\frac{1}{S_nT_{PWM}}\\
S_n=\frac{V_{in}-V_{out}}{L}K_{iv}
}$$
Kiv:電流帰還係数
プラント伝達関数の導出過程は第7回記事で解説しておりますので、良かったら読んでみて下さい。
ピーク電流モード制御の設計方法の解説
最初に書いた通り、ピーク電流モード制御の設計方法は以下の3STEPです。
- プラントの周波数特性を描く。(1次ポールになる。)
- プラントの極周波数と同じ周波数にPI制御器のゼロ点を配置する。
- DCゲインを調整して終わり。
STEP1:プラント周波数特性を描く
以下のプラント伝達関数部分だけを繋げて
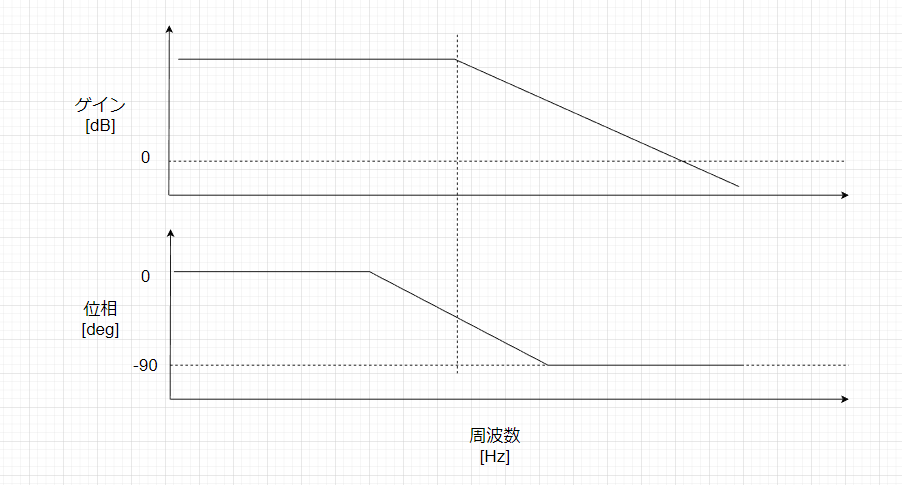
周波数特性をボード線図に描くと、以下のような1次ポールの形になります。
STEP2:プラントの極周波数と同じ周波数にPI制御器のゼロ点を配置する
PI制御器の伝達関数は以下の式になります。
$$\small{
G_{pi}=K_p\left(\frac{sT_i+1}{sT_i}\right)
}$$
そしてボード線図は以下のようになります。
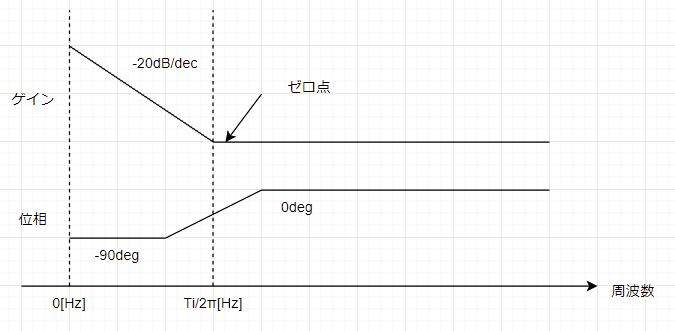
この折れ点周波数Ti/2πを先ほどの1次ポールの折れ点周波数に合わせることで、1次ポールをキャンセルします。そして残るのはPI制御器の最初の-20dB/decの減衰だけになります。
フィードバック制御込みの周波数特性は以下の通りになります。
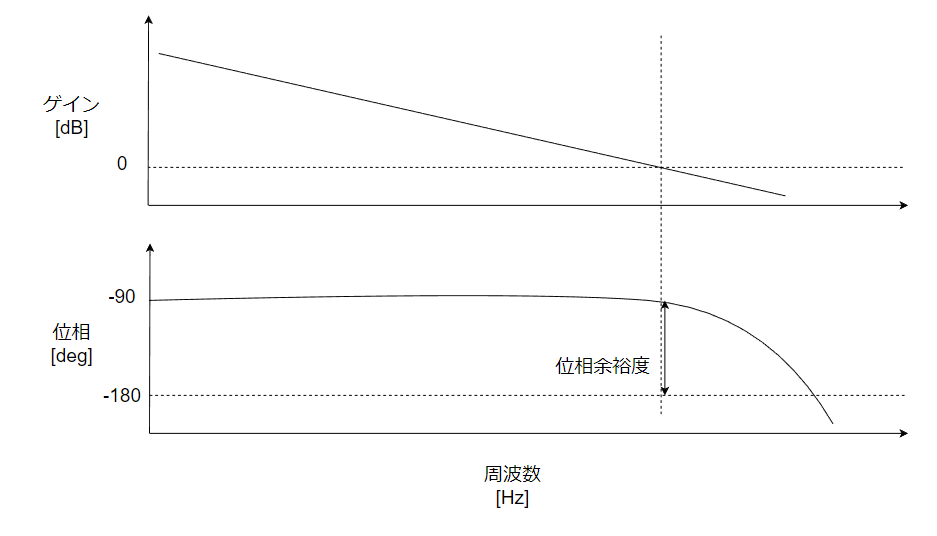
このようにゲインが直線になり、位相余裕度が90deg程度ある状態になります。
高周波領域で位相が回転しているのはPWMの無駄時間の影響です。詳しくはこちらの記事で解説しておりますので、良かったら読んでみて下さい。
STEP3:DCゲインを調整して終わり
最後に直線となったゲインを上げ下げして、所望のクロスオーバー周波数と位相余裕度を確保して設計終了です。
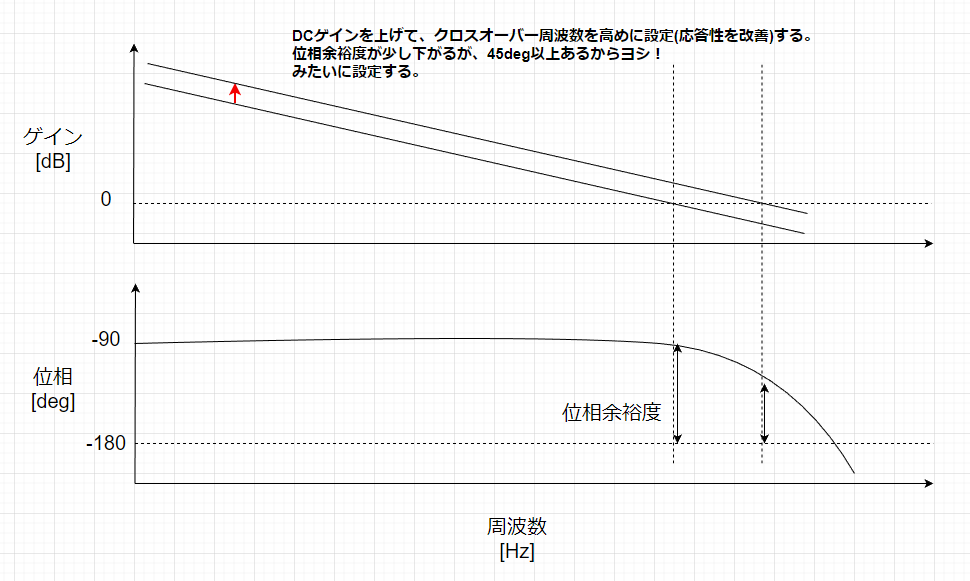
設計方法の解説は以上です。
設計具体例
具体例を設計してみて、理解を深めましょう。
この記事でパワーラインのみを設計した非絶縁降圧スイッチングレギュレータの制御設計をしてみましょう。
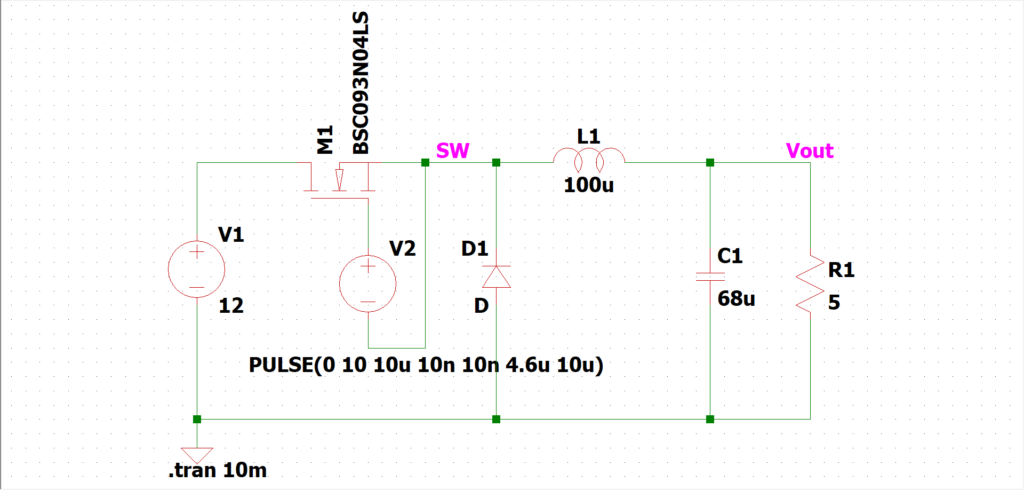
使用条件は以下の通りです。
| 項目 | 値 |
|---|---|
| 入力電圧[V] | 12 |
| 出力電圧[V] | 5 |
| 負荷電流[A] | 1 |
| スイッチング周波数[kHz] | 100 |
| 出力リップル電圧[mV] | 10 |
回路定数は見ての通り、インダクタは100μHとコンデンサは68μFです。
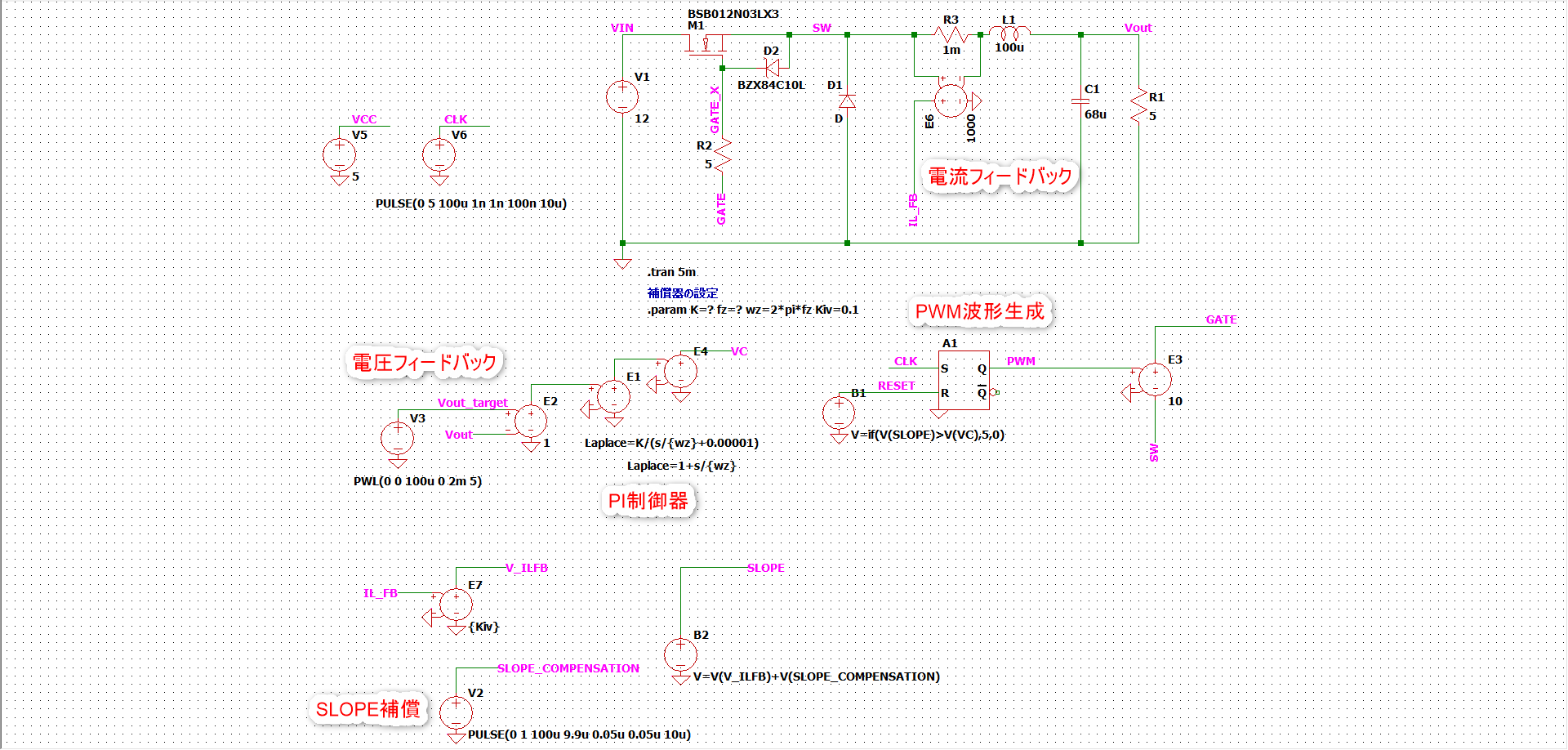
この回路にフィードバック回路を加えました↓。(電流帰還係数Kiv=0.1、スロープ補償は適当に入れてます。)
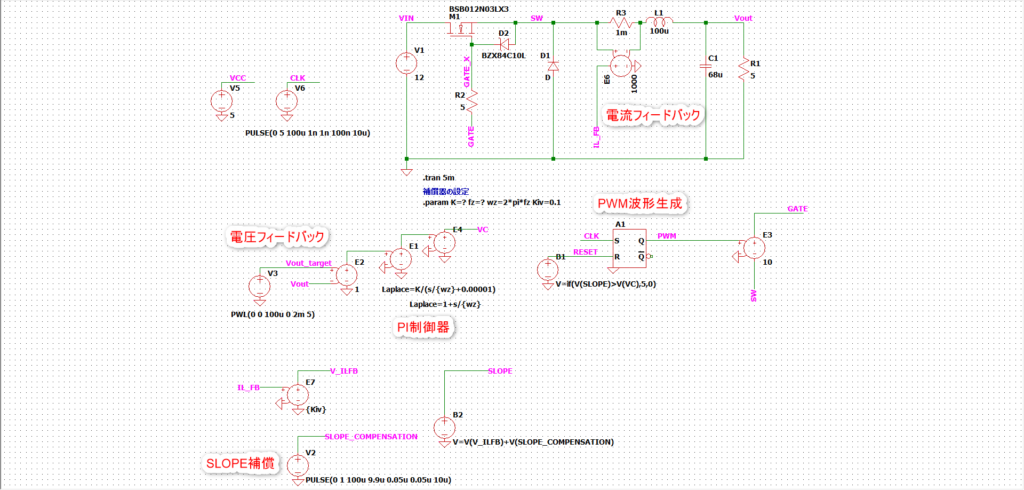
制御設計を出来るようになりたい人はここで一度読むのを止めて、K,fzはいくつに設定したらいいかを考えてみて下さい。
答えは出たでしょうか?では、制御設計してみようと思います。
プラントの周波数特性を描く
プラント周波数特性をボード線図を確認します。
pythonに計算して貰いました。その結果は以下です。
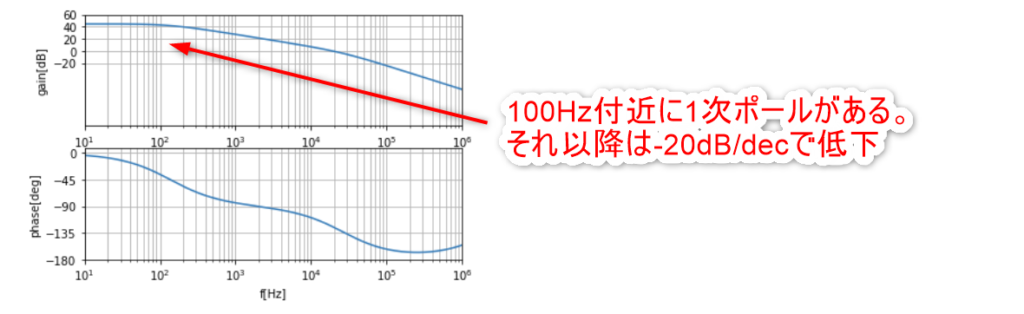
ちなみにpythonでボード線図ってどう描くの?と思った方はこちら↓の本が超オススメです。良かったら読んでみて下さい。
ちなみにちなみにこの計算を行ったpythonスクリプトは以下の通りです。
#import
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym
import control as ctl
#外部条件の設定(自分で入力する)
Vi_typ = 12.0
Vo = 5
f_pwm = 100*10**3
Ts = 1/f_pwm
Io_typ = 1
R = Vo / Io_typ
#L値とC値を設定する(自分で入力する)
L = 100 * 10 ** (-6)
r_L = 1 * 10 ** (-3)
C = 68 * 10 ** (-6)
r_C = 1 * 10 ** (-3)
#伝達関数計算
Kiv = 0.1#電流帰還率[Ω]
Sn = ((Vi_typ-Vo)/L)*Kiv#電流帰還のスロープ波形の傾き
Fm = 1/Sn/Ts#スロープ部の伝達関数
#######################################################################
#プラントの伝達関数を計算
tf_Fm = ctl.tf([Fm],[1])
tf_Kiv = ctl.tf([Kiv],[1])
tf_Gdi = ctl.tf([C*Vi_typ,0],[C*L,2*C*((r_C+r_L)/2),1])
tf_Gdv = ctl.tf([Vi_typ*C*r_C, Vi_typ],[C*L,2*C*((r_C+r_L)/2),1])
tf_ifeedback = ctl.series(tf_Kiv, tf_Gdi)
tf_plant_pre = ctl.feedback(tf_Fm,tf_ifeedback)
Gplant = ctl.series(tf_plant_pre, tf_Gdv)
#プラントのボード線図の計算
gain_plant, phase_plant, w = ctl.bode(Gplant, Plot=False)
f = w/2/np.pi#単位を[rad/sec]を[Hz]に変換
gain_plant_dB = 20*np.log10(gain_plant)#単位を[dB]に変換
phase_plant_deg = phase_plant * 180/np.pi#単位を[rad]から[deg]に変換
#plantのボード線図表示
fig, ax = plt.subplots(2,1)
ax[0].semilogx(f, gain_plant_dB)
ax[0].set_yticks([-20,0,20,40,60])
ax[0].set_xticks([10,10**2,10**3,10**4,10**5])
ax[0].grid(which = "both", axis = "x")
ax[0].grid(which = "both", axis = "y")
ax[0].set_ylabel("gain[dB]")
ax[1].semilogx(f, phase_plant_deg)
ax[1].set_yticks([-180,-135,-90,-45,0])
ax[1].set_xticks([10,10**2,10**3,10**4,10**5])
ax[1].grid(which = "both", axis = "x")
ax[1].grid(which = "both", axis = "y")
ax[1].set_ylabel("phase[deg]")
ax[1].set_xlabel("f[Hz]")プラントの極周波数にゼロ点を配置する
PI制御器のゼロ点を100Hzに設定します。ボード線図は以下の通りです。
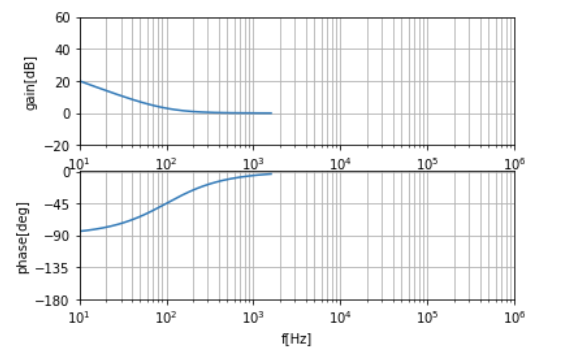
確認用のpythonスクリプトは以下の通りです。(前述のスクリプトの続きです。)
#コントローラー設計
Kp = 1
fz = 100
Ti = 1/fz/(2*np.pi)
Gc = Kp * ctl.tf([Ti, 1],[Ti, 0])
#ボード線図の計算
gain_plant, phase_plant, w = ctl.bode(Gc, Plot=False)
f = w/2/np.pi#単位を[rad/sec]を[Hz]に変換
gain_plant_dB = 20*np.log10(gain_plant)#単位を[dB]に変換
phase_plant_deg = phase_plant * 180/np.pi#単位を[rad]から[deg]に変換
#ボード線図表示
fig, ax = plt.subplots(2,1)
ax[0].semilogx(f, gain_plant_dB)
ax[0].set_yticks([-20,0,20,40,60])
ax[0].set_xlim(10, 10**6)
ax[0].grid(which = "both", axis = "x")
ax[0].grid(which = "both", axis = "y")
ax[0].set_ylabel("gain[dB]")
ax[1].semilogx(f, phase_plant_deg)
ax[1].set_yticks([-180,-135,-90,-45,0])
ax[1].set_xlim(10, 10**6)
ax[1].grid(which = "both", axis = "x")
ax[1].grid(which = "both", axis = "y")
ax[1].set_ylabel("phase[deg]")
ax[1].set_xlabel("f[Hz]")DCゲインを調整する
制御器込みの周波数特性を見てみます。同じように計算すると以下の通りになります。
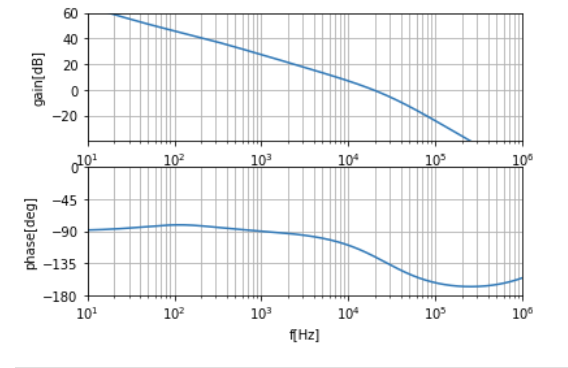
想定通りゲインの減衰の仕方が-20dB/decの一直線になってます。
クロスオーバー周波数=20kHz、位相余裕度=45deg以上が確保できていますね。
今回はDCゲインの調整はせずにこれでOKとします。
ちなみに確認用のpythonスクリプトは以下の通りです。(前述のスクリプトの続きです。)
#全体のボード線図
Gtotal = ctl.series(Gc, Gplant)
#ボード線図の計算
gain_plant, phase_plant, w = ctl.bode(Gtotal, Plot=False)
f = w/2/np.pi#単位を[rad/sec]を[Hz]に変換
gain_plant_dB = 20*np.log10(gain_plant)#単位を[dB]に変換
phase_plant_deg = phase_plant * 180/np.pi#単位を[rad]から[deg]に変換
#ボード線図表示
fig, ax = plt.subplots(2,1)
ax[0].semilogx(f, gain_plant_dB)
ax[0].set_yticks([-20,0,20,40,60])
ax[0].set_xlim(10, 10**6)
ax[0].set_ylim(-40, 60)
ax[0].grid(which = "both", axis = "x")
ax[0].grid(which = "both", axis = "y")
ax[0].set_ylabel("gain[dB]")
ax[1].semilogx(f, phase_plant_deg)
ax[1].set_yticks([-180,-135,-90,-45,0])
ax[1].set_xlim(10, 10**6)
ax[1].grid(which = "both", axis = "x")
ax[1].grid(which = "both", axis = "y")
ax[1].set_ylabel("phase[deg]")
ax[1].set_xlabel("f[Hz]")回路で動作確認
ということでPI制御器の設定は以下の通り、K=1、fz=100Hzとしました。
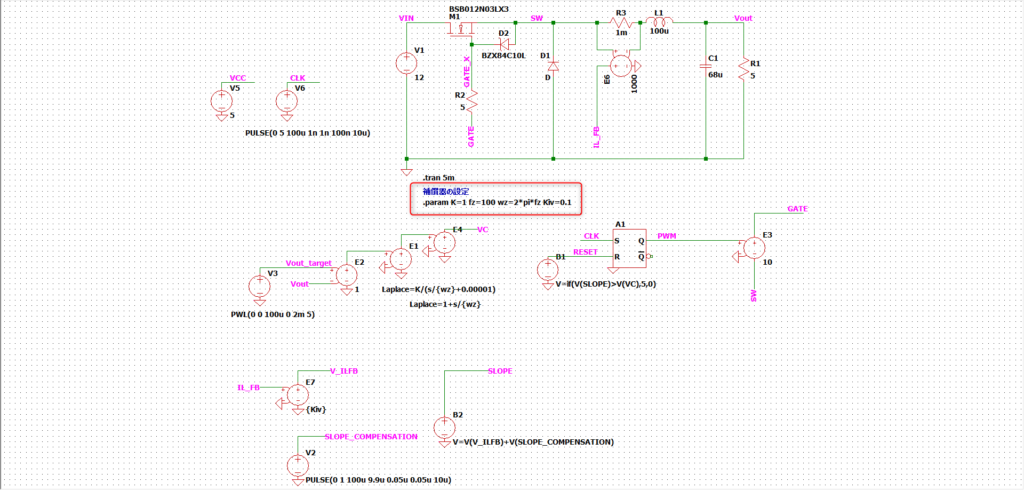
シミュレーション結果は以下の通りです。
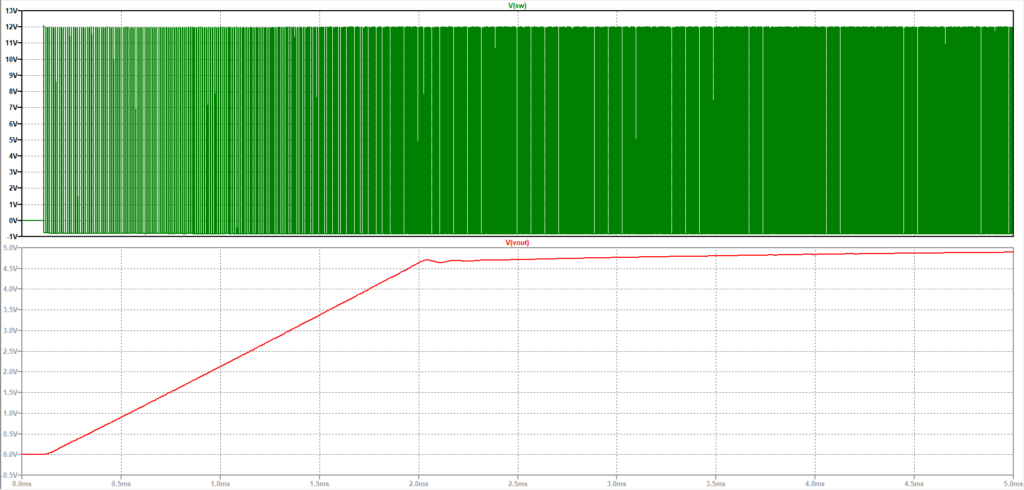
拡大します。
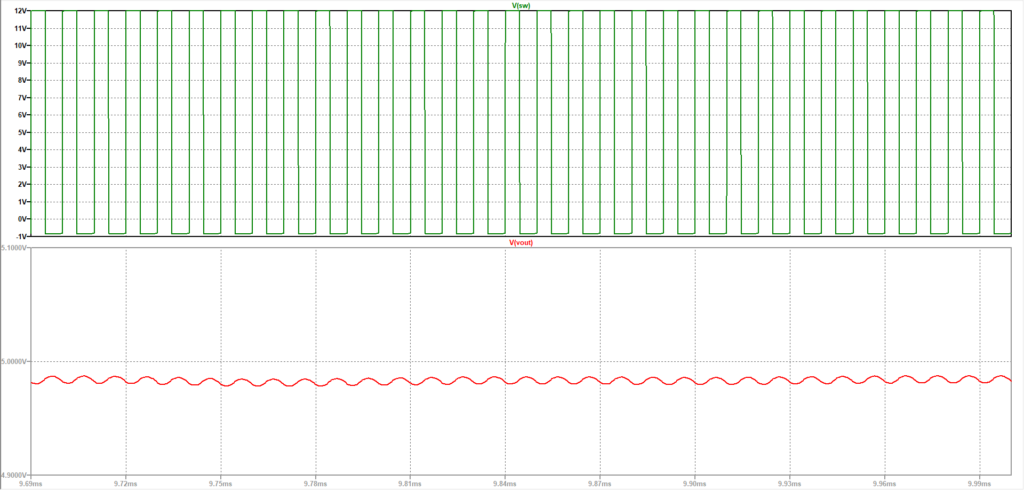
まぁとりあえず安定して動いているからいいんじゃないでしょうか(適当)。とりあえず動く状態にして各パラメータを微調整すれば良いかなと。
はい、本記事はこれで終わりです。そして、全部で9回ほど解説した非絶縁降圧スイッチングレギュレータの解説記事も今回で終わります。
何かの参考になれば幸いです。最後までお読みいただきありがとうございました!!