フルブリッジコンバータ↓の伝達関数について考えてみます。
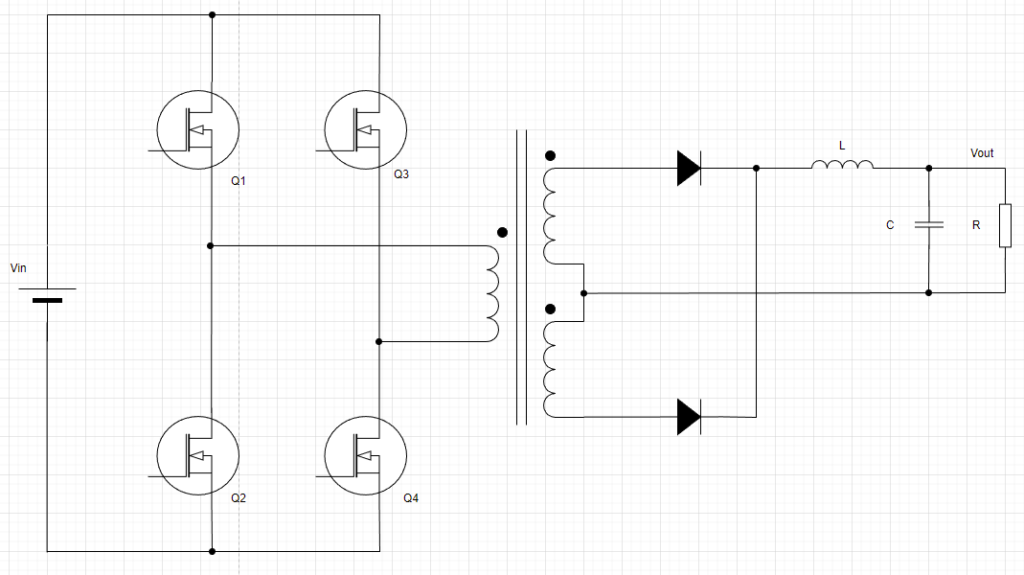
巻き線比を考慮した入力が入るってだけで非絶縁型降圧スイッチングレギュレータと同じ
フルブリッジコンバータの動作はモード1~4まであります。(フルブリッジコンバータの動作原理は過去記事で解説しております。良かったら読んでみて下さい。)
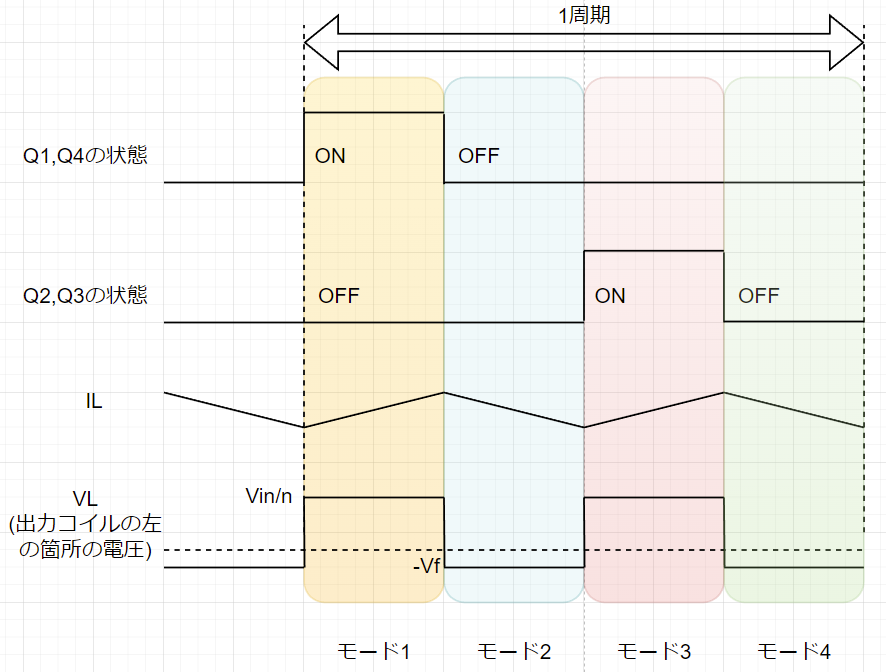
モード1とモード3がスイッチON期間でVin電圧を変圧器で巻き線比Nに応じて2次側に伝えています。
モード2とモード4がスイッチOFF期間で出力コイルに溜まったエネルギーがじわーと抜けてます。
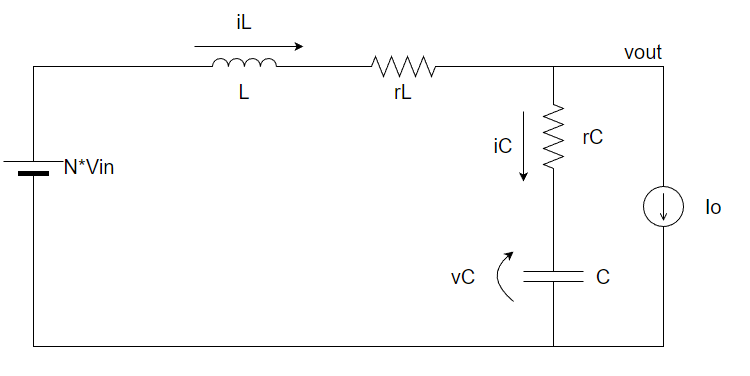
このスイッチONとスイッチOFF時の動作を簡略化して書くと
スイッチON時
スイッチOFF時
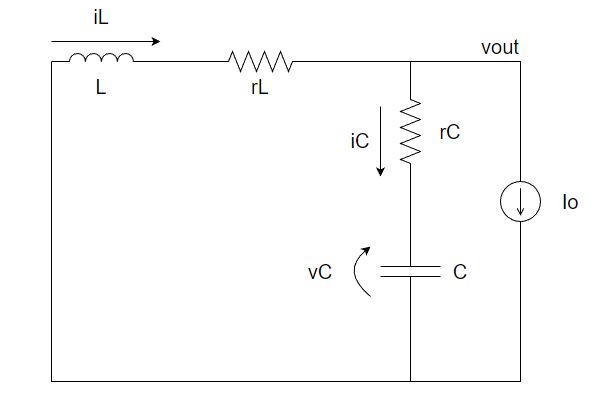
これって結局、非絶縁型降圧スイッチングレギュレータの入力電圧Vinが巻き線比Nだけ乗算されたVerだよね。ということが分かります。
変圧器の周波数特性はどう影響するのか?
これ、正直良く分かってないんですけど、たぶん気にしなくていいんじゃないかな?と思ってます。
わからないんで試しにシミュレーションしてみたんですよね。
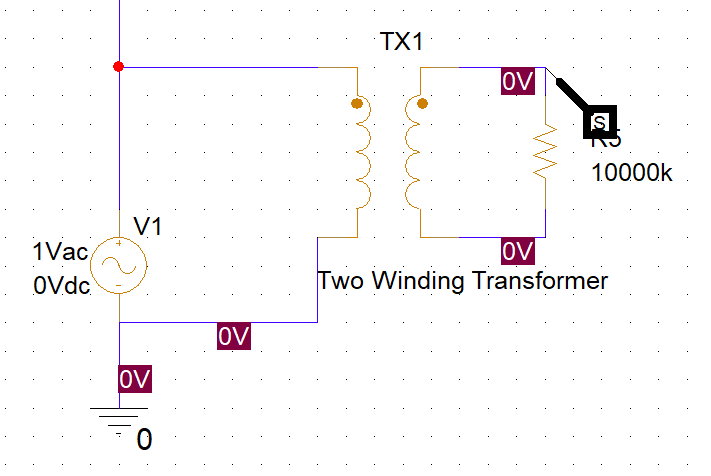
10MΩの抵抗はないと怒られるから付けてるだけ。
そしてシミュレーション結果が以下
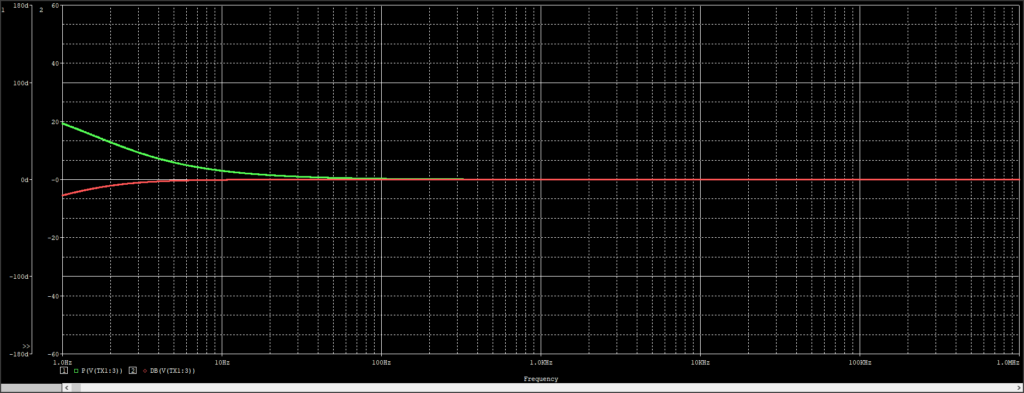
緑:位相
赤:ゲイン
何か低域のところの特性は良く分からないんですが、10Hz以降はゲインが0dB(=1)になってて、位相も0degですね。それが高域(1MHz)まで続いてます。実際制御する周波数帯域ではまぁ気にする必要ないのかな?と思っています。
つまり伝達関数はこれ
過去記事で非絶縁型降圧スイッチングレギュレータの状態空間表現は以下で
$$\small{\frac{d}{dt}\begin{bmatrix}i_L(t)\\v_C(t)\end{bmatrix}=
\begin{bmatrix}-\frac{r_L+r_C}{L}&&-\frac{1}{L}\\\frac{1}{C}&&0\end{bmatrix}\begin{bmatrix}i_L(t)\\v_C(t)\end{bmatrix}+\begin{bmatrix}\frac{Duty}{L}&&\frac{r_C}{L}\\0&&-\frac{1}{C}\end{bmatrix}\begin{bmatrix}Vin\\Io\end{bmatrix}\\
v_{out}(t)=\begin{bmatrix}r_C&&1\end{bmatrix}\begin{bmatrix}i_L(t)\\v_C(t)\end{bmatrix}+\begin{bmatrix}0&&-r_C\end{bmatrix}\begin{bmatrix}Vin\\Io\end{bmatrix}}$$
Dutyに対する出力電圧とコイル電流の伝達関数は以下のようになると導出しました。
$$\small{\frac{ΔVout(s)}{ΔDuty}=G_{dv}=\frac{1}{P(s)} \left( 1+\frac{s}{ω_{esr}} \right) Vin}$$
$$\small{\frac{ΔIL(s)}{ΔDuty}=G_{di}=\frac{C*Vin*s}{P(s)}}$$
ただし
$$\small{P(s)=\frac{s^2}{ω_n^2}+\frac{2δ}{ω_n}s+1}$$
$$\small{ω_n=\frac{1}{\sqrt{LC}},δ=\frac{r_L+r_C}{2}\sqrt{\frac{C}{L}},ωesr=\frac{1}{Cr_C}}$$
Vin:入力電圧[V]、Vout:出力電圧[V]、Duty:スイッチングON DUTY[%]、L:出力コイルインダクタンス値[H]、C:出力コンデンサ容量値[F]、r_L:インダクタのDCR[Ω]、r_C:コンデンサのESR[Ω]、Io:出力電流[A]
このVin->N*Vinになったものが絶縁型フルブリッジコンバータの状態空間表現であり、伝達関数ということですね。
つまり
$$\small{\frac{d}{dt}\begin{bmatrix}i_L(t)\\v_C(t)\end{bmatrix}=
\begin{bmatrix}-\frac{r_L+r_C}{L}&&-\frac{1}{L}\\\frac{1}{C}&&0\end{bmatrix}\begin{bmatrix}i_L(t)\\v_C(t)\end{bmatrix}+\begin{bmatrix}\frac{Duty}{L}&&\frac{r_C}{L}\\0&&-\frac{1}{C}\end{bmatrix}\begin{bmatrix}N*Vin\\Io\end{bmatrix}\\
v_{out}(t)=\begin{bmatrix}r_C&&1\end{bmatrix}\begin{bmatrix}i_L(t)\\v_C(t)\end{bmatrix}+\begin{bmatrix}0&&-r_C\end{bmatrix}\begin{bmatrix}N*Vin\\Io\end{bmatrix}}$$
N:巻き線比
$$\small{\frac{ΔVout(s)}{ΔDuty}=G_{dv}=\frac{1}{P(s)} \left( 1+\frac{s}{ω_{esr}} \right) N*Vin}$$
$$\small{\frac{ΔIL(s)}{ΔDuty}=G_{di}=\frac{C*N*Vin*s}{P(s)}}$$
はい、本記事は以上になります。誰かの参考になれば幸いです。
他にもグダグダとフルブリッジコンバータ関連の記事を書いておりますので、良かったら読んでみて下さい。
1回目:【電源回路】フルブリッジコンバータの動作原理
2回目:【電源回路】フルブリッジコンバータの動作をシミュレーションで理解する
3回目:【電源回路】電圧モード制御フルブリッジコンバータの動作モデルを作った
4回目:【電源回路】フルブリッジコンバータの伝達関数(本記事)
5回目:【電源回路】電流モード制御フルブリッジコンバータの動作モデルを作った
最後までお読みいただきありがとうございました!!


