皆様、お疲れ様です。
本記事では昇圧dcdcコンバータの制御設計をやってみたご報告を致します。今回はその第一回目、「プラントの伝達関数」について理解します。
具体的にはプラント伝達関数がどんな式になるのか?その特性を確認します。特性から
- 昇圧dcdcの制御系が難しすぎて理解できない!!
- 昇圧dcdcを設計したい!!
とお考えの方の参考になれば幸いです。また本記事は以下の書籍の影響を多大に受けております。

スイッチング電源制御設計の基礎posted with ヨメレバ安部征哉/財津俊行 日経BP 2015年03月06日頃 楽天ブックスで購入Amazonで購入
今では絶版でめっちゃ高級本です。それだけめちゃくちゃ良書です。図書館へGO!!!
では始めます。
まず昇圧回路ってどんなんよ?
過去に電圧モード制御の昇圧dcdcを設計しておりますのでそちらの記事を参照下さい。
こんな回路です↓。
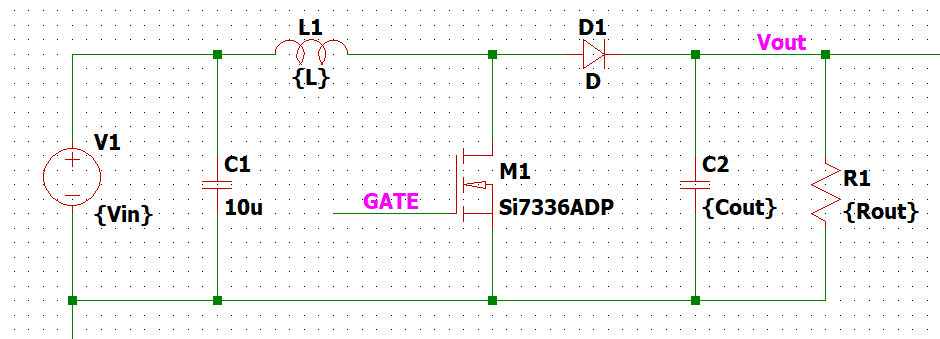
M1のスイッチがON/OFFを繰り返すことにより入力電圧より高い電圧をVoutに出力します。原理も説明すると大変なので、本記事は伝達関数にフォーカスします。
電流モード制御とは?
DCDCの主な制御モードには電圧モード制御と電流モード制御があります。筆者は電圧モード制御の発展版と理解しています。
| 制御 | フィードバック | 特徴 |
|---|---|---|
| 電圧モード | 出力電圧 | LCの2次のポールで位相が180°回転 |
| 電流モード | 出力電圧+コイル電流 | LCの2次ポールが打ち消されて1次のポールになる |
電流モード制御のメリットは電圧モードでネックとなっていたLCの2次のポールが打ち消されて一次のポールだけが見えることです。これにより、位相補償の設計が簡単になっています。
なんで打ち消されんの?というのはプラント伝達関数をしこしこと計算していくと分かる感じですね。
ブロック線図
電流モード制御の昇圧dcdcのブロック線図は以下の通りです。今回は点線で囲われたプラント伝達関数を見ていきます。
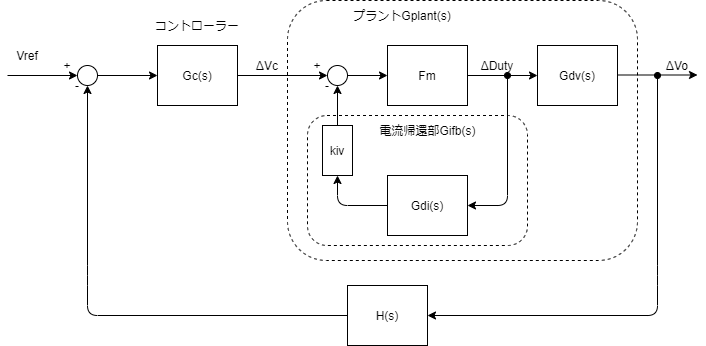
Gdv:dutyを出力電圧に変換している伝達関数
Gdi:dutyをコイル電流に変換している伝達関数
kiv:フィードバックした電流を電圧に変える係数
Fm:電圧をDutyに変換する
これらを一括りにしたものがプラントの伝達関数です。
私たちが設計すべきなのはコントローラーGc(s)です。
系全体はどういう風に動くか?
電圧をフィードバックしてH(s)で変換
↓
基準電圧Vrefと比較してコントローラーGc(s)で次のDUTYを計算
↓
出力電圧をいい感じに調整
って感じに動きます。
プラント伝達関数はこれ
これです↓。
$$G_{plant}(s)=\frac{Fm}{1+FmG_{di}(s)K_iv}G_{dv}(s)$$
Gdv(s) Gdi(s)は以下の通りの式となります。
$$G_{dv}(s)=\frac{V_i}{D’^2}\frac{(1+\frac{s}{ω_{esr}})(1-\frac{s}{ω_{RHP-z}})}{P(s)}$$
$$G_{di}(s)=\frac{\frac{I_o}{D’^2}(1+\frac{s}{ω_0})}{P(s)}$$
ただし
$$P(s)=1+2δ\frac{s}{ω_n}+(\frac{s}{ω_n})^2$$
$$D’=1-D、δ=\frac{r_L+D’r_c}{2D’}\sqrt{\frac{C}{L}}、ω_n=\frac{D’}{\sqrt{LC}}$$
$$ω_{RHP-z}=\frac{1}{LI_o}\frac{V_i^2}{V_o}、ω_0=\frac{I_o}{CV_o}、ω_{esr}=\frac{1}{Cr_c}$$
$$Fm=\frac{1}{S_n*T_{PWM}}$$
$$S_n=\frac{V_{i}}{L}K_{iv}$$
$$D’=1-D$$
$$D=\frac{V_o}{V_i}$$
D:PWM DUTY[%]
C:出力コンデンサ容量値[F]
rC:コイルのESR[Ω]
L:出力インダクタ値[H]
Vi:入力電圧[V]
Io:出力電流[A]
Vo:出力電圧[V]
Tpwm:PWM周期[sec]
kiv:電流帰還係数
はい。どうでしょうか。吐きそうでしょうか?これでも実は簡略化した式です。吐きそうですね。でもこれからプラント伝達関数を計算するといい感じに色々消えてくれます。
何でこの式になるんだよ!!!と思った方には申し訳ありません。筆者は導出過程はわかっていません。賢い人が解いたらこうなると認識しています。状態平均化法でうにゃうにゃ解いていったらこうなるらしいです。
GdiやらGdvはごちゃごちゃ解いたらこうなるといっても、さすがにGplantがなんでこうなるのくらいは解説します。最初のブロック線図を順番に合成していけば自然とGplantが導き出されます。
Gdi(s)とkivはひとまとめにする。
まずはGidとkivをまとめます。
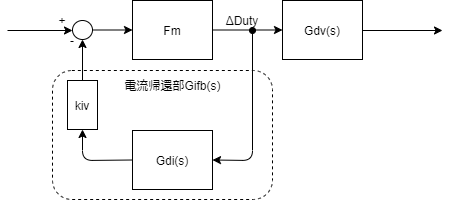
直列結合なので掛け算です。
$$G_{ifb}(s)=kiv*Gdi(s)$$
ブロック線図は↓こうなります。
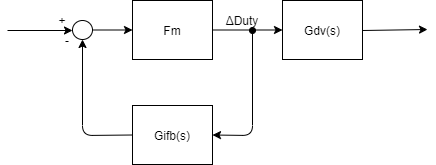
FmとGplant_feedbackをひとまとめにする。
フィードバック結合なので
$$G_{plant-pre}(s)=\frac{Fm}{1+Fm*G_{ifb}(s)}$$
$$G_{plant-pre}(s)=\frac{Fm}{1+Fm*kiv*Gdi(s)}$$
ブロック線図は↓こうなります。

Gdv(s)を結合をひとまとめにする。
直列結合なので掛け算です。
$$G_{plant}(s)=G_{plant-pre}(s)*Gdv(s)$$
$$G_{plant}(s)= \frac{Fm}{1+Fm*kiv*Gdi(s)}*Gdv(s)$$
これがプラント伝達関数です。実際は手計算する必要なんて全然ないです。文明の利器matlabやpythonなどの計算機を利用して楽に計算しましょう。
Gplantの特性はどうなるの?何で1次ポールに見えるの?
Gplantはなぜ1次ポールに見えるのか?それはGplantにGdi,Gdvを入れてがちゃがちゃ計算したらわかります。吐きそうなのを我慢して計算してみましょう。
$$G_{plant}(s)= \frac{Fm}{1+Fm*kiv*Gdi(s)}*Gdv(s)$$
Gdi,Gdvを代入する前に1<<Fm*kiv*Gdi(s)なので、1を省略します↓。Fmが消えますね。
$$G_{plant}(s)= \frac{Fm}{Fm*kiv*Gdi(s)}*Gdv(s)$$
$$G_{plant}(s)= \frac{1}{kiv*Gdi(s)}*Gdv(s)$$
勇気を出してGdi,Gdvを代入します。ここでP(s)とD’^2が消えますね。
$$G_{plant}(s)= \frac{1}{kiv* \frac{\frac{I_o}{D’^2}(1+\frac{s}{ω_0})}{P(s)}}* \frac{V_i}{D’^2}\frac{(1+\frac{s}{ω_{esr}})(1-\frac{s}{ω_{RHP-z}})}{P(s)}$$
$$G_{plant}(s)= \frac{1}{kiv*I_o(1+\frac{s}{ω_0})}* V_i(1+\frac{s}{ω_{esr}})(1-\frac{s}{ω_{RHP-z}})$$
ちょっと整理しましょう。
$$G_{plant}(s)= \frac{V_i}{I_okiv}\frac{(1+\frac{s}{ω_{esr}})(1-\frac{s}{ω_{RHP-z}})}{(1+\frac{s}{ω_0})}$$
これで大体終わりです。おいおいどこが1次なんだ?って思うかもしれませんが、分子の2つのゼロ点wesrとwrhpzは無視です。無視。なぜかというと、この二つの周波数は計算すると、だいぶ高い周波数なんです。実際制御する帯域は低い帯域(数10kHz~数100kHzまで)で関係するのはw0の方なので、もう無視でいいじゃんって感じです。となると、気にしたらいいのはw0の方で良いじゃんって感じです。
ボード線図はこんな感じ
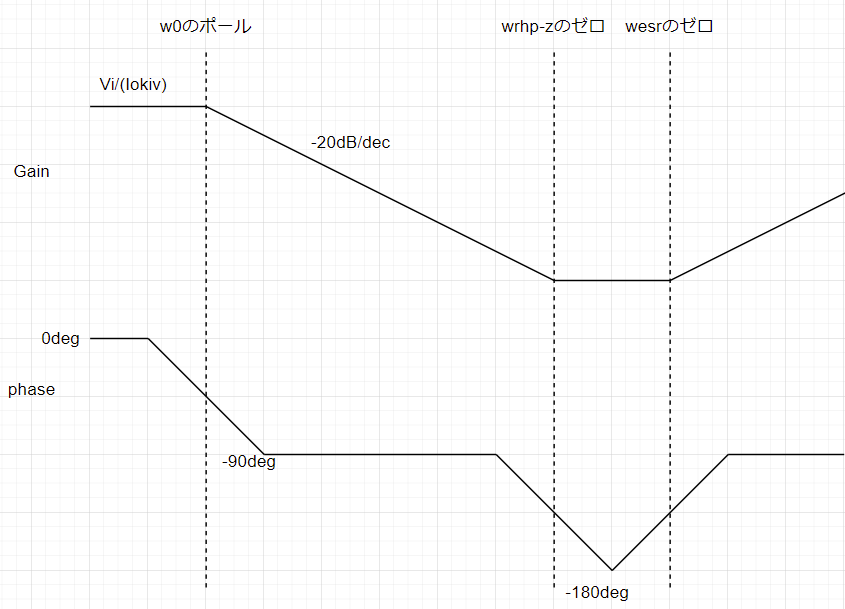
ややこしいwrhp-zとwesrの奴らより手前で制御を設計しましょうよ。そしたらプラントは1次のポールでしょ。簡単でしょ。っていう感じですね。
今日はこれで終わりです。次回はこの特性を加味して電流モード制御の昇圧コンバータの制御設計をしてみようと思います。
以上です。最後までお読みいただきありがとうございました!

