少し前に降圧スイッチングレギュレータの伝達関数を状態平均化法を使って計算しました。
今回は以下のような昇圧スイッチングレギュレータの伝達関数を状態平均化法を用いて導出します。
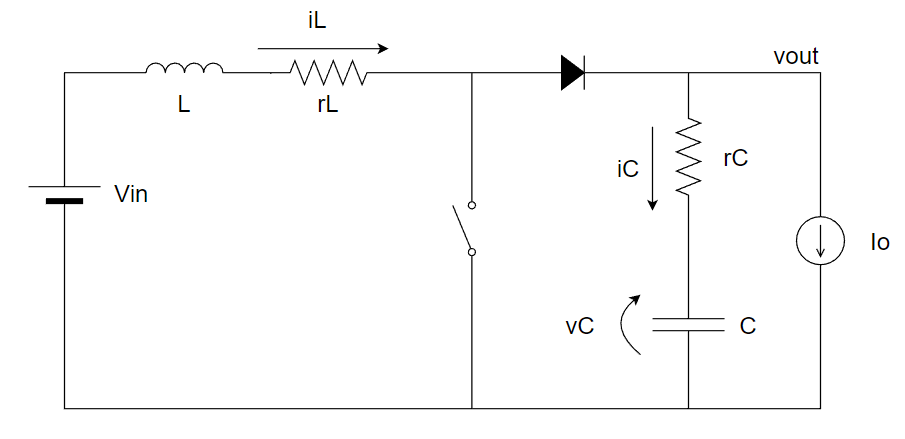
- 昇圧スイッチングレギュレータの伝達関数
- 状態平均化法を使った導出方法
- その計算過程
スイッチングレギュレータの制御設計をしたり、動作モデルを作ったりするのに便利な知識ですので、良かったら読んでみて下さい。
答えだけ知りたいよ!という方に先に導出結果の伝達関数を提示しておきます。
Dutyの変化による出力電圧の変化に関する伝達関数は以下の通り
$$\scriptsize{
G_{dv}(s)=\frac{-s^2LCr_CIo+s(D’r_CCVin-(L+(2r_Lr_C+D’r_C^2)C)Io)+D’Vin-(2r_L+D’r_C)Io}
{P(s)D’^3}
}$$
Dutyの変化による出力コイル電流に関する伝達関数は以下の通り
$$\small{
G_{di}(s)=\frac{s\frac{C}{D’^4}(D’Vin-r_LIo)+\frac{1}{D’^2}Io}{P(s)}
}$$
ただし
$$\small{P(s)=\left(\frac{s}{ω_n}\right)^2+s\frac{2δ}{ω_n}+1}$$
$$\small{ω_n=\frac{D’}{\sqrt{LC}}}$$
$$\small{δ=\frac{r_C+D’r_C}{2D’}\sqrt{\frac{C}{L}}}$$
Vin:入力電圧[V]、Vout:出力電圧[V]、Duty:スイッチングON DUTY[%]、L:出力コイルインダクタンス値[H]、C:出力コンデンサ容量値[F]、r_L:インダクタのDCR[Ω]、r_C:コンデンサのESR[Ω]、Io:出力電流[A]、D’=1-Duty
導出までの流れを最初に書いておきます。
- スイッチONとOFFのときの回路方程式を書き出す。
- 1の方程式を状態変数=(iL,vc)、入力=(Vin,Io)、出力=(vout)の状態空間表現で書き直す。
iL:コイル電流、vc:コンデンサ電圧、Vin:入力電圧、Io:出力電流、vout:出力電圧 - 2のONとOFFのときの状態空間表現をDutyで加重平均する。
- 定常解を求める。
- 定常状態から微小変動が生じたときの式にする。
- 5の式をラプラス変換する。
- 6の式を整理してΔvout/ΔDとΔIL/ΔDの伝達関数を得る。
では、やってみましょう。
スイッチONとOFFのときの回路方程式を書き出す
スイッチON時
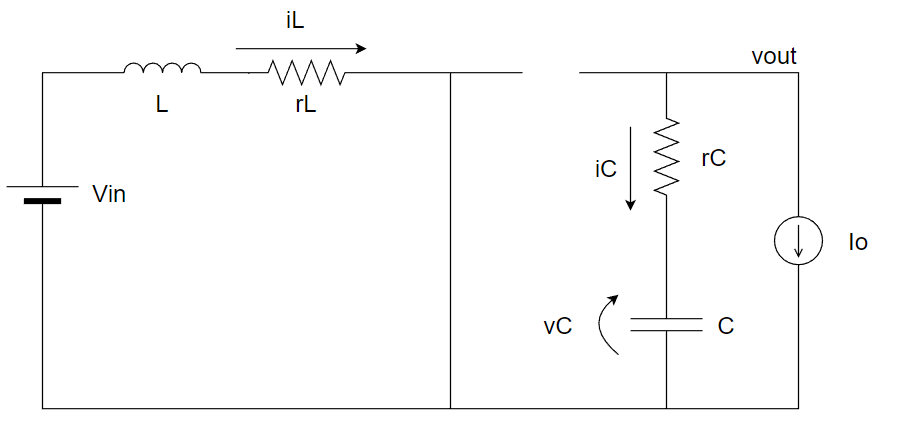
$$\small{Vin=i_L(t)r_L+L\frac{di_L(t)}{dt}}\tag{1}$$
$$\small{i_C(t)=-Io}\tag{2}$$
$$\small{i_C(t)=C\frac{dv_C(t)}{dt}}\tag{3}$$
$$\small{v_{out}(t)=v_C(t)+i_C(t)r_C}\tag{4}$$
スイッチOFF時
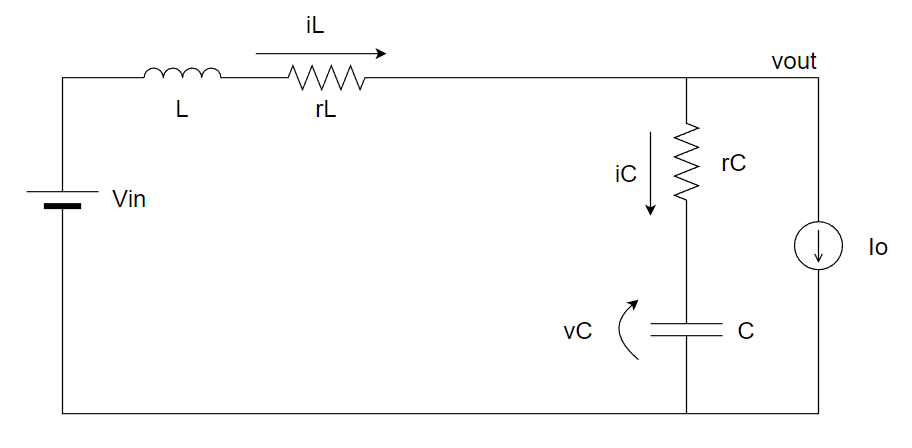
$$\small{Vin=i_L(t)r_L+L\frac{di_L(t)}{dt}+r_Ci_C(t)+v_C(t)}\tag{5}$$
$$\small{i_C(t)+Io=i_L(t)}\tag{6}$$
$$\small{i_C(t)=C\frac{dv_C(t)}{dt}}\tag{7}$$
$$\small{v_{out}(t)=v_C(t)+i_C(t)r_C}\tag{8}$$
回路方程式を状態空間表現に書き直す
状態空間表現は以下のような式です。
\begin{eqnarray}
\small{\dot{x}(t)=Ax(t)+Bu(t)\\
y(t)=Cx(t)+Du(t)}
\end{eqnarray}
これに状態変数xと入力uと出力yをそれぞれ以下とします。
$$\small{x(t)=\begin{bmatrix}
i_L(t)\\
v_C(t)
\end{bmatrix},u(t)=\begin{bmatrix}
Vin\\
Io
\end{bmatrix},y(t)=v_{out}(t)}$$
回路方程式を行列表現できるように変換していきます。
スイッチON時
まず(1)式をdiL/dt=にします。
$$\small{L\frac{di_L(t)}{dt}=Vin-i_L(t)r_L}$$
$$\small{\frac{di_L(t)}{dt}=-\frac{r_L}{L}i_L(t)+\frac{1}{L}Vin}$$
(3)式に(2)式を代入して以下を得ます。
$$\small{-Io=C\frac{dv_C(t)}{dt}}$$
$$\small{\frac{dv_C(t)}{dt}=-\frac{Io}{C}}$$
(4)式に(2)式を代入して以下を得ます。
$$\small{v_{out}(t)=v_C(t)-r_CIo}$$
以上よりスイッチON時の状態空間表現は以下の通りになります。
$$\small{
\begin{bmatrix}\dot{i_L(t)}\\ \dot{v_C(t)}\end{bmatrix}=
\begin{bmatrix}
-\frac{r_L}{L}&&0\\
0&&0\end{bmatrix}
\begin{bmatrix}i_L(t)\\v_C(t)\end{bmatrix}
+\begin{bmatrix}
\frac{1}{L}&&0\\0&&-\frac{1}{C}
\end{bmatrix}
\begin{bmatrix}Vin\\Io\end{bmatrix}\\
v_{out}(t)=\begin{bmatrix}0&&1\end{bmatrix}
\begin{bmatrix}i_L(t)\\v_C(t)\end{bmatrix}
+\begin{bmatrix}0&&-r_C\end{bmatrix}
\begin{bmatrix}Vin\\Io\end{bmatrix}
}\tag{9}$$
あ~もういや。次がスイッチOFF時です。
スイッチOFF時
まず(5)式をdiL/dt=にします。
$$\small{L\frac{di_L(t)}{dt}=-r_Li_L(t)-v_C(t)+Vin-r_Ci_C(t)}$$
(6)式を代入してic(t)を消します。
$$\small{L\frac{di_L(t)}{dt}=-r_Li_L(t)-v_C(t)+Vin-r_C(i_L(t)-Io)}$$
$$\small{L\frac{di_L(t)}{dt}=-(r_L+r_C)i_L(t)-v_C(t)+Vin-r_CIo)}$$
Lで割る。
$$\small{L\frac{di_L(t)}{dt}=-\frac{r_L+r_C}{L}i_L(t)-\frac{1}{L}v_C(t)+\frac{1}{L}Vin-\frac{r_C}{L}Io}$$
(7)式に(6)式を代入してic(t)を消して、dvc(t)/dt=に直します。
$$\small{i_L(t)-Io=C\frac{dv_C(t)}{dt}}$$
$$\small{\frac{dv_C(t)}{dt}=\frac{1}{C}i_L(t)-\frac{1}{C}Io}$$
(8)式に(6)式を代入してic(t)を消して、以下を得ます。
$$\small{v_{out}(t)=r_Ci_L(t)+v_C(t)-r_CIo}$$
以上よりスイッチOFF時の状態空間表現は以下の通りになります。
$$\small{
\begin{bmatrix}\dot{i_L(t)}\\ \dot{v_C(t)}\end{bmatrix}=
\begin{bmatrix}
-\frac{r_L+r_C}{L}&&-1\\
\frac{1}{C}&&0\end{bmatrix}
\begin{bmatrix}i_L(t)\\v_C(t)\end{bmatrix}
+\begin{bmatrix}
1&&-r_C\\0&&-\frac{1}{C}
\end{bmatrix}
\begin{bmatrix}Vin\\Io\end{bmatrix}\\
v_{out}(t)=\begin{bmatrix}r_C&&1\end{bmatrix}
\begin{bmatrix}i_L(t)\\v_C(t)\end{bmatrix}
+\begin{bmatrix}0&&-r_C\end{bmatrix}
\begin{bmatrix}Vin\\Io\end{bmatrix}
}\tag{10}$$
はぁ疲れましたね。スイッチON/OFF時のそれぞれの状態空間表現をまとめると以下になります。
| SW=ON | $$\small{ \begin{bmatrix}\dot{i_L(t)}\\ \dot{v_C(t)}\end{bmatrix}= \begin{bmatrix} -\frac{r_L}{L}&&0\\ 0&&0\end{bmatrix} \begin{bmatrix}i_L(t)\\v_C(t)\end{bmatrix} +\begin{bmatrix} \frac{1}{L}&&0\\0&&-\frac{1}{C} \end{bmatrix} \begin{bmatrix}Vin\\Io\end{bmatrix}\\ v_{out}(t)=\begin{bmatrix}0&&1\end{bmatrix} \begin{bmatrix}i_L(t)\\v_C(t)\end{bmatrix} +\begin{bmatrix}0&&-r_C\end{bmatrix} \begin{bmatrix}Vin\\Io\end{bmatrix} }\tag{9}$$ |
| SW=OFF | $$\small{ \begin{bmatrix}\dot{i_L(t)}\\ \dot{v_C(t)}\end{bmatrix}= \begin{bmatrix} -\frac{r_L+r_C}{L}&&-1\\ \frac{1}{C}&&0\end{bmatrix} \begin{bmatrix}i_L(t)\\v_C(t)\end{bmatrix} +\begin{bmatrix} 1&&-r_C\\0&&-\frac{1}{C} \end{bmatrix} \begin{bmatrix}Vin\\Io\end{bmatrix}\\ v_{out}(t)=\begin{bmatrix}r_C&&1\end{bmatrix} \begin{bmatrix}i_L(t)\\v_C(t)\end{bmatrix} +\begin{bmatrix}0&&-r_C\end{bmatrix} \begin{bmatrix}Vin\\Io\end{bmatrix} }\tag{10}$$ |
$$\small{A_{ON}=\begin{bmatrix}-\frac{r_L}{L}&&0\\0&&0\end{bmatrix},
A_{OFF}=\begin{bmatrix}-\frac{r_L+r_C}{L}&&-1\\\frac{1}{C}&&0\end{bmatrix}\\
B_{ON}=\begin{bmatrix}\frac{1}{L}&&0\\0&&-\frac{1}{C}\end{bmatrix},
B_{OFF}=\begin{bmatrix}1&&-r_C\\0&&-\frac{1}{C}\end{bmatrix}\\
C_{ON}=\begin{bmatrix}0&&1\end{bmatrix},
C_{OFF}=\begin{bmatrix}r_C&&1\end{bmatrix}\\
D_{ON}=\begin{bmatrix}0&&-r_C\end{bmatrix},
D_{OFF}=\begin{bmatrix}0&&-r_C\end{bmatrix}}$$
これをDUTYで平均を取ります。
ONとOFFのときの状態空間表現をDutyで加重平均する
DUTYで平均を取ります。具体的には
$$\small{A=Duty*A_{ON}+(1-Duty)*A_{OFF}\\
B=Duty*B_{ON}+(1-Duty)*B_{OFF}\\
C=Duty*C_{ON}+(1-Duty)*C_{OFF}\\
D=Duty*D_{ON}+(1-Duty)*D_{OFF}}$$
をします。1-Duty=D’とします。
$$\small{
A=\begin{bmatrix}-\frac{r_L+D’r_C}{L}&&-\frac{D’}{L}\\\frac{D’}{C}&&0\end{bmatrix}\\
B=\begin{bmatrix}\frac{1}{L}&&\frac{D’r_C}{L}\\0&&-\frac{1}{C}\end{bmatrix}\\
C=\begin{bmatrix}D’r_C&&1\end{bmatrix}\\
D=\begin{bmatrix}0&&-r_C\end{bmatrix}
}$$
つまり状態平均化法した昇圧コンバータの状態空間表現は以下になります。
$$\small{
\begin{bmatrix}\dot{i_L(t)}\\ \dot{v_C(t)}\end{bmatrix}=
\begin{bmatrix}-\frac{r_L+D’r_C}{L}&&-\frac{D’}{L}\\\frac{D’}{C}&&0\end{bmatrix}
\begin{bmatrix}i_L(t)\\v_C(t)\end{bmatrix}
+\begin{bmatrix}\frac{1}{L}&&\frac{D’r_C}{L}\\0&&-\frac{1}{C}\end{bmatrix}
\begin{bmatrix}Vin\\Io\end{bmatrix}\\
v_{out}(t)=\begin{bmatrix}D’r_C&&1\end{bmatrix}
\begin{bmatrix}i_L(t)\\v_C(t)\end{bmatrix}
+\begin{bmatrix}0&&-r_C\end{bmatrix}
\begin{bmatrix}Vin\\Io\end{bmatrix}
}$$
ふぅーーー。これでオッケーです。プラントはこの式で計算すれば動作を模擬できます。
ではこれから伝達関数を求めていきます。
定常解を求める
$$\dot{x(t)}=0$$のときを計算します。
計算結果は良く見る形になります。
計算過程は単純なので省略しますが、定常解は以下になります。
$$\small{V_{out}=\frac{1}{D’}Vin-Io\left(-r_C+\frac{r_L+D’r_C}{D’^2}\right)}$$
$$\small{I_L=\frac{Io}{D’}}$$
定常状態の状態空間表現を大文字で書き直すと、、、
\begin{eqnarray}
\small{\dot{X}(t)=AX(t)+BU(t)}\\
\small{Y(t)=CX(t)+DU(t)}
\end{eqnarray}
これに微小変動が生じたときを考えると伝達関数を導くことが出来ます。
定常状態から微小変動が生じたときの式にする
ここは全く降圧スイッチングレギュレータと同じですが、
この式↓を微小変動が発生した時を考えます。微小変動は+Δで表現します。
$$\small{\dot{X}(t)=AX(t)+BU(t)}$$
$$\small{\dot{X}(t)+Δ\dot{X}(t)=(A+ΔA)(X(t)+ΔX(t))+(B+ΔB)(U(t)+ΔU(t))}$$
展開します。
$$\scriptsize{\dot{X}(t)+Δ\dot{X}(t)=AX(t)+AΔX(t)+ΔAX(t)+ΔAΔX(t)+BU(t)+BΔU(t)+ΔBU(t)+ΔBΔU(t)}$$
微小項(Δ*Δ)の項目はちっちゃいので無視します。
$$\scriptsize{\dot{X}(t)+Δ\dot{X}(t)=AX(t)+AΔX(t)+ΔAX(t)+BU(t)+BΔU(t)+ΔBU(t)}$$
ここで見たいのは定常解から変動が起きたときにどうなるか?を知りたいので、静特性(定常解)部分は無視します。つまり
$$\small{\dot{X}(t)=AX(t)+BU(t)}$$
部分は消します。
$$\small{Δ\dot{X}(t)=AΔX(t)+ΔAX(t)+BΔU(t)+ΔBU(t)}$$
ΔAについて考えます。AはDutyを変数とした関数です。なのでDutyで偏微分したものがΔAになります。
$$\small{Δ\dot{X}(t)=AΔX(t)+\frac{\partial A}{\partial Duty}X(t)+BΔU(t)+ΔBU(t)}$$
ΔBについて考えます。BもDutyを変数とした関数です。なのでDutyで偏微分したものがΔBになります。
$$\small{Δ\dot{X}(t)=AΔX(t)+\frac{\partial A}{\partial Duty}ΔDX(t)+BΔU(t)+\frac{\partial B}{\partial Duty}ΔDU(t)}\tag{11}$$
同様にY(t)=Vout(t)についても微小変動を起こした時
$$\scriptsize{Vout(t)+ΔVout(t)=(C+ΔC)(X(t)+ΔX(t))+(D+ΔD)(U(t)+ΔU(t))\\
Vout(t)+ΔVout(t)=CX(t)+CΔX(t)+ΔCX(t)+ΔCΔX(t)+DU(t)+DΔU(t)+ΔDU(t)+ΔDΔU(t)}$$
同様に微小変動ΔΔは無視します。
$$\scriptsize{Vout(t)+ΔVout(t)=CX(t)+CΔX(t)+ΔCX(t)+DU(t)+DΔU(t)+ΔDU(t)}$$
同様に定常解のVout(t)=CX(t)+DU(t)は消します。
$$\small{ΔVout(t)=CΔX(t)+ΔCX(t)+DΔU(t)+ΔDU(t)}$$
CはDutyを変数とした関数です。なのでDutyで偏微分したものがΔAになります。
Dは定数なので、微分したら0です。なのでΔDも0です。
$$\small{ΔVout(t)=CΔX(t)++\frac{\partial C}{\partial Duty}ΔDX(t)+DΔU(t)}\tag{12}$$
(11),(12)式をまとめると微小変動が生じたとき内部状態や出力の変化量は以下の式で求まります。
\begin{eqnarray}
\small{Δ\dot{X}(t)=AΔX(t)+\frac{\partial A}{\partial D}ΔDX(t)+BΔU(t)+\frac{\partial B}{\partial D}ΔDU(t)}\\
\small{ΔVout(t)=CΔX(t)++\frac{\partial C}{\partial D}ΔDX(t)+DΔU(t)}
\end{eqnarray}
ラプラス変換して式を整理
上の式をラプラス変換します。
\begin{eqnarray}
\small{sIΔX(s)=AΔX(s)+\frac{\partial A}{\partial D}ΔD(s)X(s)+BΔU(s)+\frac{\partial B}{\partial D}ΔD(s)U(s)}\\
\small{ΔVout(s)=CΔX(s)++\frac{\partial C}{\partial D}ΔD(s)X(s)+DΔU(s)}
\end{eqnarray}
$$\small{ΔX(s)=(sI-A)^{-1}(\frac{\partial A}{\partial D}ΔD(s)X(s)+BΔU(s)+\frac{\partial B}{\partial D}ΔD(s)U(s))}\tag{13}$$
(13)式のsI-Aをまず解いてみます。
$$\small{sI-A=\begin{bmatrix}s&&0\\0&&s\end{bmatrix}
-\begin{bmatrix}-\frac{r_L+D’r_C}{L}&&-\frac{D’}{L}\\\frac{D’}{C}&&0\end{bmatrix}\\
=\begin{bmatrix}s+\frac{r_L+D’r_C}{L}&&\frac{D’}{L}\\-\frac{D’}{C}&&s\end{bmatrix}}$$
(sI-A)^-1を計算します。↑の逆行
$$\small{(sI-A)^{-1}=\frac{1}{ad-bc}\begin{bmatrix}s&&\ -\frac{D’}{L}\\ \frac{D’}{C}&&s+\frac{r_L+D’r_C}{L}\end{bmatrix}}$$
逆行列の先頭1/(ad-bc)を計算します。
$$\scriptsize{ad-bc=\left(\left(s+\frac{r_L+D’r_C}{L}\right)*s+\frac{D’^2}{LC}\right)=s^2+\frac{r_L+D’r_C}{L}s+\frac{D’^2}{LC}}$$
これを戻しますね。
$$\small{(sI-A)^{-1}=
\begin{bmatrix}
\frac{sLC}{s^2LC+sC(r_L+D’r_C)+D’^2}&&\ \frac{D’C}{s^2LC+sC(r_L+D’r_C)+D’^2}\\
\frac{D’L}{s^2LC+sC(r_L+D’r_C)+D’^2}&&\frac{(sL+r_L+D’r_C)C}{s^2LC+sC(r_L+D’r_C)+D’^2}
\end{bmatrix}\\
=\frac{1}{P(s)}
\begin{bmatrix}
\frac{sLC}{D’^2}&& -\frac{C}{D’}\\
\frac{L}{D’}&&\frac{(sL+r_L+D’r_C)C}{D’^2}
\end{bmatrix}}$$
$$\small{P(s)=s^2\frac{LC}{D’^2}+s\frac{C(r_L+D’r_C)}{D’^2}+1}$$
$$\small{P(s)=\left(\frac{s}{ω_n}\right)^2+s\frac{2δ}{ω_n}+1}$$
$$\small{ω_n=\frac{D’}{\sqrt{LC}}}$$
$$\small{δ=\frac{r_C+D’r_C}{2D’}\sqrt{\frac{C}{L}}}$$
これで(13)式の前半ちょっとが解けました。ここで(13)式を見て、ΔDで括ってみます。
$$\small{ΔX(s)=(sI-A)^{-1}\left(\left(\frac{\partial A}{\partial D}X(s)+\frac{\partial B}{\partial D}U(s)\right)ΔD(s)+BΔU(s)\right)}$$
ΔU(s)=[ΔVin ΔIo]なので制御対象ではなくて外乱です。今回は制御対象のDutyに着目しましょう。したがって、
$$\small{ΔX(s)=(sI-A)^{-1}\left(\left(\frac{\partial A}{\partial D}X(s)+\frac{\partial B}{\partial D}U(s)\right)ΔD(s)\right)}\tag{14}$$
ここでAとBをそれぞれDutyで偏微分します。
$$\small{
\frac{\partial A}{\partial D}=\frac{\partial}{\partial D}\begin{bmatrix}-\frac{r_L+(1-D)r_C}{L}&&-\frac{1-D}{L}\\\frac{1-D}{C}&&0\end{bmatrix}
=\begin{bmatrix}\frac{r_C}{L}&&\frac{1}{L}\\-\frac{1}{C}&&0\end{bmatrix}}$$
$$\small{
\frac{\partial B}{\partial D}=\frac{\partial}{\partial D}\begin{bmatrix}\frac{1}{L}&&\frac{(1-D)r_C}{L}\\0&&-\frac{1}{C}\end{bmatrix}
=\begin{bmatrix}0&&\frac{-r_C}{L}\\0&&0\end{bmatrix}
}$$
これを元の式(14)に戻します。
$$\small{ΔX(s)=(sI-A)^{-1}
\left(\left(\begin{bmatrix}\frac{r_C}{L}&&\frac{1}{L}\\-\frac{1}{C}&&0\end{bmatrix}X(s)
+\begin{bmatrix}0&&\frac{-r_C}{L}\\0&&0\end{bmatrix}U(s)\right)ΔD(s)\right)}$$
U(s)はVinとIoだけど、Vinは全部0が掛けられるから消えて、Ioだけが残る。X(s)は[iL vc]の定常解。
$$\small{\frac{ΔX(s)}{ΔD(s)}=(sI-A)^{-1}
\left(\begin{bmatrix}\frac{r_C}{L}&&\frac{1}{L}\\-\frac{1}{C}&&0\end{bmatrix}
\begin{bmatrix}I_L(s)\\V_C(s)\end{bmatrix}
+\begin{bmatrix}\frac{-r_C}{L}\\0\end{bmatrix}Io\right)}$$
(sI-A)^-1を入れてみましょうか。
$$\small{
\frac{ΔX(s)}{ΔD(s)}=
\frac{1}{P(s)}
\begin{bmatrix}
\frac{sLC}{D’^2}&& -\frac{C}{D’}\\
\frac{L}{D’}&&\frac{(sL+r_L+D’r_C)C}{D’^2}
\end{bmatrix}
\left(\begin{bmatrix}\frac{r_C}{L}&&\frac{1}{L}\\-\frac{1}{C}&&0\end{bmatrix}
\begin{bmatrix}I_L(s)\\V_C(s)\end{bmatrix}
+\begin{bmatrix}\frac{-r_C}{L}\\0\end{bmatrix}Io\right)
}$$
ILとVCは定常解なのでそれを代入します。
$$\scriptsize{
\frac{ΔX(s)}{ΔD(s)}=
\frac{1}{P(s)}
\begin{bmatrix}
\frac{sLC}{D’^2}&& -\frac{C}{D’}\\
\frac{L}{D’}&&\frac{(sL+r_L+D’r_C)C}{D’^2}
\end{bmatrix}
\left(\begin{bmatrix}\frac{r_C}{L}&&\frac{1}{L}\\-\frac{1}{C}&&0\end{bmatrix}
\begin{bmatrix}\frac{Io}{D’}\\\frac{1}{D’}Vin-Io\left(-r_C+\frac{r_L+D’r_C}{D’^2}\right)\end{bmatrix}
+\begin{bmatrix}\frac{-r_C}{L}\\0\end{bmatrix}Io\right)
}$$
これを展開して整理すると以下の式を得ます。
$$\small{
\frac{ΔX(s)}{ΔD(s)}=
\frac{1}{P(s)}
\begin{bmatrix}
s\frac{C}{D’^4}(D’Vin-r_LIo)+\frac{1}{D’^2}Io\\
-s\frac{L}{D’^3}Io+\frac{1}{D’^2}(Vin-r_CIo)-\frac{2r_L}{D’^3}Io
\end{bmatrix}
}$$
これの上側だけ取ればDutyの変化量によるIL電流の変化量Gdiが求まります。
$$\small{
G_{di}(s)=\frac{s\frac{C}{D’^4}(D’Vin-r_LIo)+\frac{1}{D’^2}Io}{P(s)}\tag{15}
}$$
さて、つぎはΔVoutについて解いてみます。
$$\small{ΔVout(t)=CΔX(t)++\frac{\partial C}{\partial D}ΔDX(t)+DΔU(t)}$$
今見たいのはΔDutyに対する変動なのでΔUは外乱なので削除します。
ΔDutyで割りますかね。
$$\small{\frac{ΔVout(t)}{ΔD}=C\frac{ΔX(t)}{ΔD}+\frac{\partial C}{\partial D}X}$$
行列CをDutyで偏微分します。
$$\small{
\frac{\partial C}{\partial D}=\frac{\partial}{\partial D}\begin{bmatrix}(1-D)r_C&&1\end{bmatrix}=\begin{bmatrix}-r_C&&0\end{bmatrix}
}$$
戻します。
$$\small{\frac{ΔVout(t)}{ΔD}=C\frac{ΔX(t)}{ΔD}+\begin{bmatrix}-r_C&&0\end{bmatrix}X}$$
忘れてましたが、ラプラス変換します。
$$\small{\frac{ΔVout(s)}{ΔD(s)}=C\frac{ΔX(s)}{ΔD(s)}+\begin{bmatrix}-r_C&&0\end{bmatrix}X}$$
X/Sは計算していますので、代入します。Xは定常解を代入します。
$$\scriptsize{
\frac{ΔVout(s)}{ΔD(s)}=\begin{bmatrix}D’r_C&&1\end{bmatrix}
\frac{1}{P(s)}
\begin{bmatrix}
s\frac{C}{D’^4}(D’Vin-r_LIo)+\frac{1}{D’^2}Io\\
-s\frac{L}{D’^3}Io+\frac{1}{D’^2}(Vin-r_CIo)-\frac{2r_L}{D’^3}Io
\end{bmatrix}\\
+\begin{bmatrix}-r_C&&0\end{bmatrix}\begin{bmatrix}\frac{Io}{D’}\\\frac{1}{D’}Vin-Io\left(-r_C+\frac{r_L+D’r_C}{D’^2}\right)\end{bmatrix}
}$$
これを整理すると以下を得ます。
$$\scriptsize{
G_{dv}(s)=\frac{ΔVout(s)}{ΔD(s)}\\
=\frac{-s^2LCr_CIo+s(D’r_CCVin-(L+(2r_Lr_C+D’r_C^2)C)Io)+D’Vin-(2r_L+D’r_C)Io}
{P(s)D’^3}\tag{16}
}$$
やっと終わりました。はい、以上で本記事は終わりです。
たぶん未来の自分しか読まないと思いますが、、、
最後までお読みいただきありがとうございました!誰かの参考になれば幸いです。


