みなさま、お疲れ様です。
今回は単相インバーターに関する記事です。
1回目:【インバーター】バイポーラSPWM制御単相インバーターの動作原理
2回目:【インバーター】バイポーラSPWM制御単相インバーターのプラント伝達関数を計算する
3回目:【インバーター】バイポーラSPWM制御単相インバーターの動作をLTspiceで確認する
4回目:【インバーター】【インバーター】プラントGdiの周波数特性をLTspiceで確認する
5回目:【インバーター】単相インバーターの制御設計をしてみる【PR制御】
6回目:【インバーター】単相インバーターのリップル電流の求め方(本記事)
今回の記事は単相インバーターのリアクトル電流のお話です。
- インバーターのリアクトルリップル電流はどう計算したらいいかわからない。
- 実験でリアクトル電流を見ると出力交流の半分くらいでピーク値になったけど、なぜかわからない。
と悩みをお持ちの方の解決になると思います。
リアクトルリップル電流の計算式とその導出過程、またピーク値の求め方までを解説します。
では、始めます。
【結論】単相インバーターのリップル電流計算式
早速結論ですが、単相インバーターのリップル電流は以下の式で計算できます。
$$\small{
ΔI_L=\frac{V_{DC}T_{SW}}{L}(1-msin(ωt))msin(ωt)
}$$
ΔIL:リアクトルリップル電流[A]、VDC:入力直流電圧[V]、Tsw:スイッチング周期[sec]、m:モジュレーションインデックス(変調率)
更にΔILのピーク値は以下の式で計算できます。
$$\small{
ΔI_{Lpeak}=\frac{V_{DC}T_{SW}}{4L}
}$$
なんでこの式になるの?について、導出過程を以下に示します。
導出過程
まず、パワエレの最重要の式(=リアクトルの式)から始めます。
$$\small{
ΔI_L=\frac{V_L}{L}Δt
}$$
インバーターのスイッチがONしているとき、つまりリアクトルにエネルギー供給時を考えます。
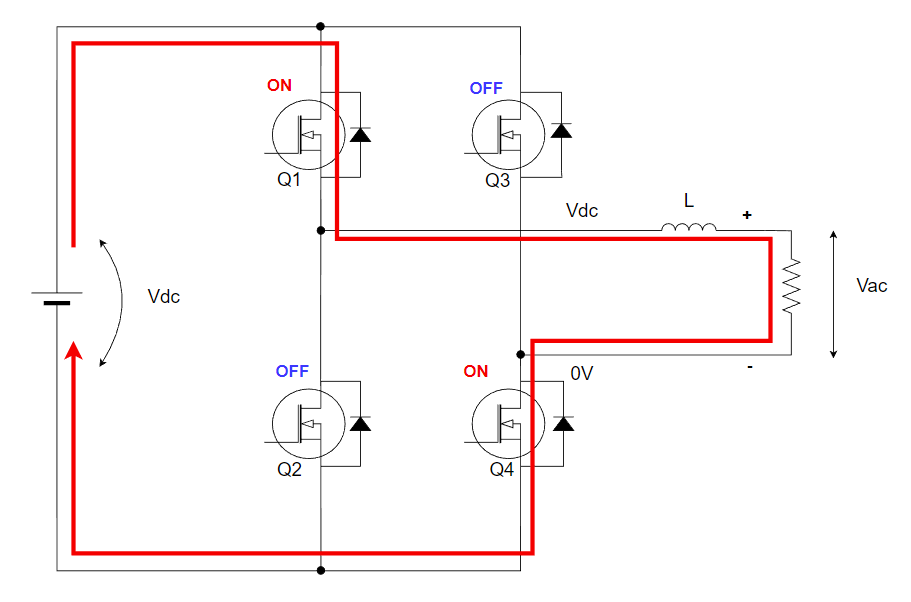
(LにはVdc-Vacの電圧がかかる。)
ちなみに詳しい動作解説はこちらの記事
リアクトルにはVDC – Vacの電圧がかかってます。したがって以下の式に変形します。
$$\small{
ΔI_L=\frac{V_{DC}-V_{ac}}{L}Δt
}$$
Δt=Duty*Tswを使って表せるので代入します。
$$\small{
ΔI_L=\frac{V_{DC}-V_{ac}}{L}DT_{sw}
}$$
Duty=Vac/Vdcなので、代入します。
$$\small{
ΔI_L=\frac{V_{DC}-DV_{DC}}{L}DT_{sw}
}$$
さて、Dutyというのはインバーターでは出力電圧が正弦波(=sin)になるように時々刻々と変化しています。このDutyは以下の式で表せます。
$$\small{
D=msin(ωt)
}$$
m:変調率、ω=2πf
それを代入すると以下の式になります。
$$\small{
ΔI_L=\frac{V_{DC}-msin(ωt)V_{DC}}{L}msin(ωt)T_{sw}
}$$
いい感じに括ると最初の式が現れます。
$$\small{
ΔI_L=\frac{V_{DC}T_{SW}}{L}(1-msin(ωt))msin(ωt)
}$$
ΔILの式をグラフにして見る
式をパッと見ただけでは分かりづらいので、グラフにして見ました。
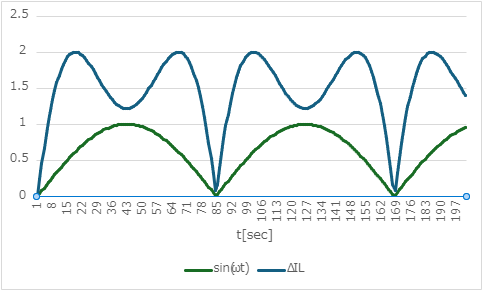
緑線:sin(ωt)
上側半サイクル、下側半サイクルとやってることは同じなので、絶対値で表示しています。
このグラフを見ると、sin(ωt)の実効値付近でΔILのピークを迎えて、sin(ωt)のピーク付近でΔILが小さくなっています。
実際にインバーターのリップル電流を見たことある方はなんとなくイメージと合うのではないでしょうか。
「なんで出力交流電圧の実効値付近でリップル電流が大きくなるの?なんで?ねぇなんで?え?そゆとこを疑問に思わないとダメなんじゃないの?ねぇねぇ。」
と先輩が詰めて来たとしても、冷静に
「いや、理論式通りに動いてるだけでしょ。むしろ何がわからないんですか?」
と返しましょう。
微分して=0を解くとΔILのピーク値が求められる
ピーク値を求めたいと思ったとき、以下のグラフの頂点がピーク値ですね。
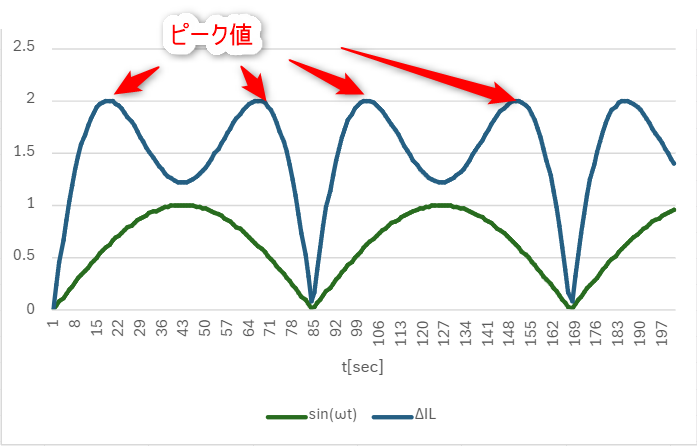
つまり傾き=0を求めるとピーク値が求められるということになります。
では、先ほどのΔILの式を微分してみます。
$$\small{
ΔI_L’=\left( \frac{V_{DC}T_{SW}}{L} \left( 1-msin(ωt) \right)msin(ωt) \right)’
}$$
項を分けます。
$$\small{
ΔI_L’=\frac{V_{DC}T_{SW}}{L}m(sin(ωt))’-\frac{V_{DC}T_{SW}}{L}m^2(sin^2(ωt))’
}$$
sinの微分をしたらいい感じです。(sinωt)’=ωcos(ωt)、(sin^2ωt)’=2ωsin(ωt)cos(ωt)です。
$$\small{
ΔI_L’=\frac{V_{DC}T_{SW}}{L}mωcos(ωt)-\frac{V_{DC}T_{SW}}{L}m^22ωsin(ωt)cos(ωt)
}$$
ΔI_L’=0を解きます。
$$\small{
\frac{V_{DC}T_{SW}}{L}mωcos(ωt)-\frac{V_{DC}T_{SW}}{L}m^22ωsin(ωt)cos(ωt)=0
}$$
移行して、共通の部分を消すと以下の簡単な式になります。
$$\small{
1=m2sin(ωt)
}$$
sin(ωt)=の形にすると以下のようになります。
$$\small{
sin(ωt)=\frac{1}{2m}
}$$
つまり、sin(ωt)=1/2mのときにΔILはピーク値になるということです。ではΔILの式にこれを代入します。
$$\small{
ΔI_L=\frac{V_{DC}T_{SW}}{L}(1-msin(ωt))msin(ωt)\\
ΔI_L=\frac{V_{DC}T_{SW}}{L}(1-m\frac{1}{2m})m\frac{1}{2m}
}$$
mを消して、整理すると以下のようになります。
$$\small{
ΔI_L=\frac{V_{DC}T_{SW}}{4L}
}$$
これで最初に提示した式の二つ目が出てきました。
素晴らしいですね。この式でピーク値を計算できます。この式を使えば、「リアクトル値をいくつにしたらピーク値をある値以下に出来ますね。」って設計出来ますね!
はい、これで本記事を終わります。
誰かの参考になれば幸いです。最後までお読みいただきありがとうございました!!!

