どうも。最近LTspiceで伝達関数の計算が出来る!ってことを初めて知ったのでその内容とやり方を解説します。
何かの参考になれば幸いです。
先に結論を言ってしまうと
・回路コンポーネント「e」を使う。
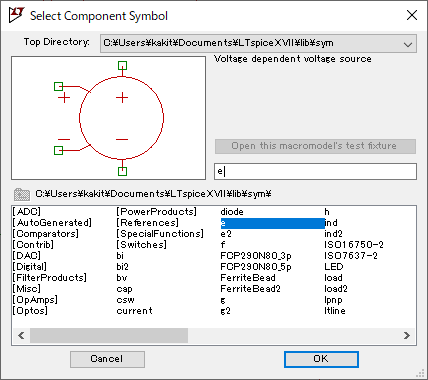
・この「e」に”laplace=~”と伝達関数を記述すると記述した伝達関数で「e」が動作する。
・ただ2次以上になると正しく計算できない。。。
です。
RCフィルタの1次遅れ回路とLCフィルタの2次遅れ回路を例に出しながら解説します。
RCフィルタの伝達関数表現
先にRCフィルタがどんなんかを見てみましょう。こんなんです。↓
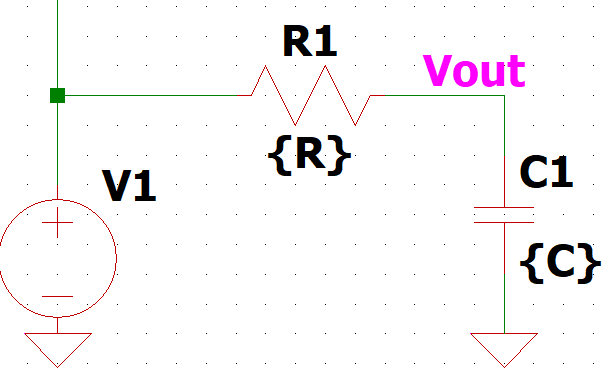
RとCがあり、V1の電圧変化をVoutに伝えるときにちょっとゆっくり立ち上げる効果があります。
そのゆっくり度合いを計算するのに活躍するのが伝達関数なんですね。
今回はR=10Ω、C=1uFの回路を対象にしてみます。
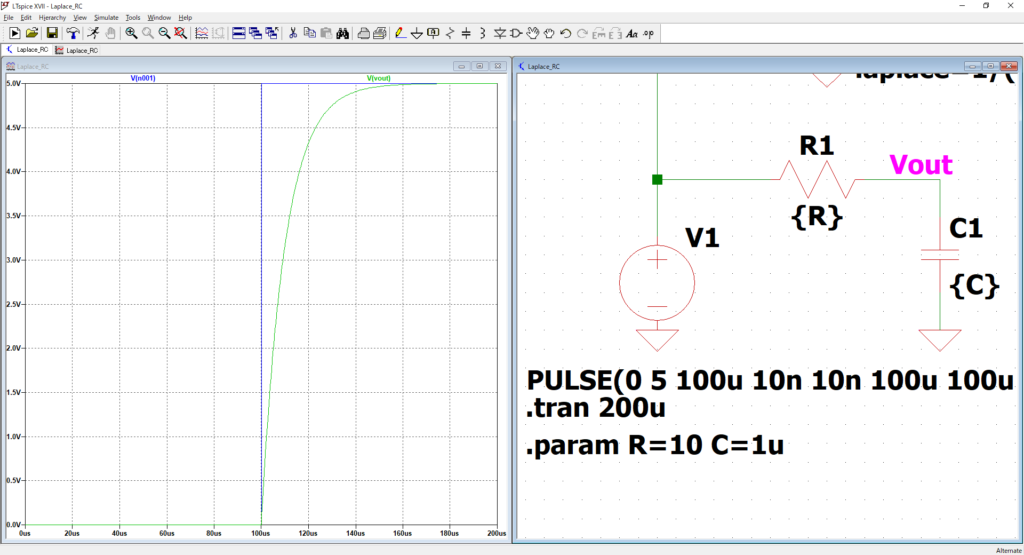
回路図中の”.pram ~”でRCの値を設定しています。
波形を見ると、V1のステップ入力に対して、ちょっとなまった波形が出力されています。
まずは伝達関数を計算する
伝達関数=出力/入力で表現されるので、これを計算していきます。
まずRとCをそれぞれ周波数領域に持っていきます。いわゆるラプラス変換ですね。
RはそのままRで、Cは1/sCとなります。こんなイメージです↓。ラプラス変換後は回路素子はZとして捉えましょう。

このときのVoutを計算しようとすると単純にRと1/sCの分圧になりますね。
つまり
$$V_{out}=\frac{\frac{1}{sC}}{R+\frac{1}{sC}}*V1$$
分子分母にsCを掛けます。
$$V_{out}=\frac{1}{1+sCR}*V1$$
V1を移項して完成です。
$$G(s)=\frac{V_{out}}{V1}=\frac{1}{1+sCR}$$
伝達関数を書いてみる
まず回路エディタで「e」を持ってきましょう。Slect Component Symbolから選択します。

配置したら部品の上で右クリックします。
そこのValueのところに”laplace=1/(1+10*1u*s)”と入力しましょう。
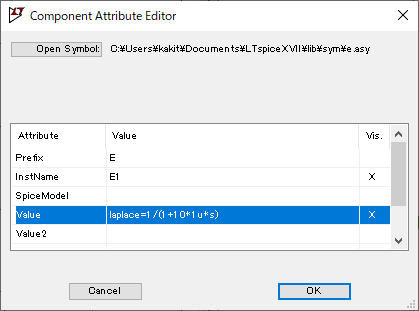
これでOKです。
動作確認
では動作を見てみましょう。
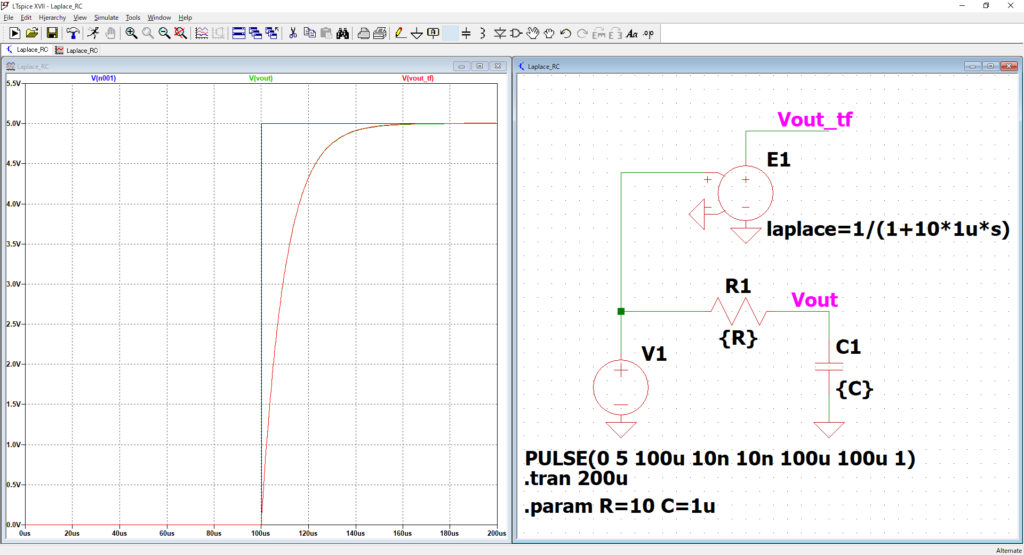
赤と緑が重なっていますね。完璧です。
ちなみにパラメータ化もできる
laplace=1/(1+{R}*{C}*s)と記入すると.paramで設定した値で動いてくれるので、楽です。
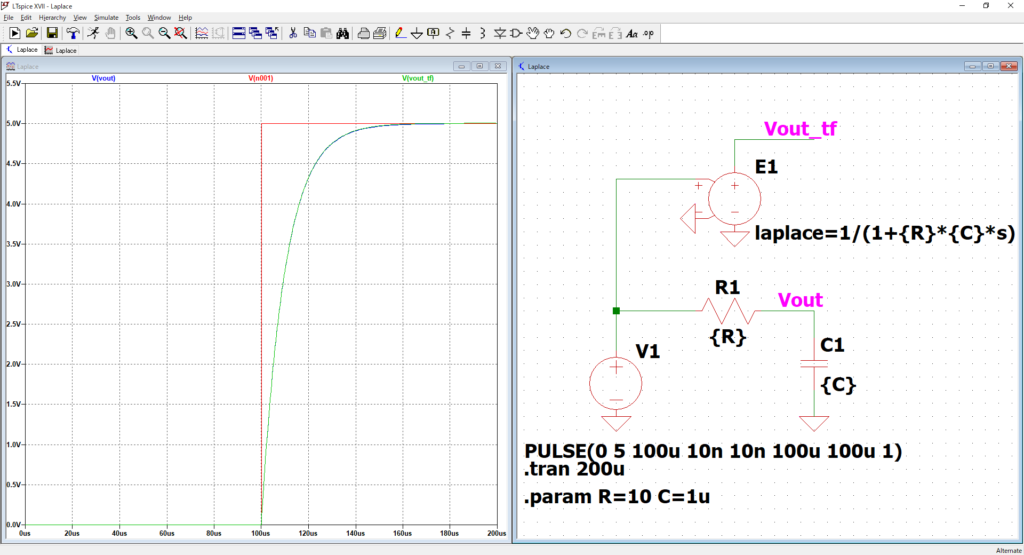
LCフィルタの伝達関数表現
LCフィルタはこんなんです。↓
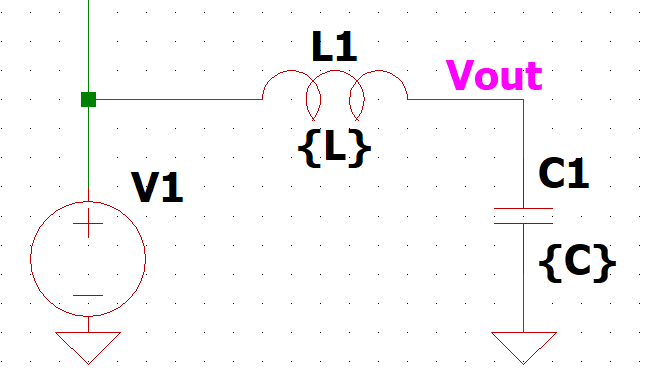
RC同様、V1の電圧変化をVoutに伝えるときにちょっとゆっくり立ち上げる効果があります。
今回はL=10uH、C=1uFの回路を対象にしてみます。
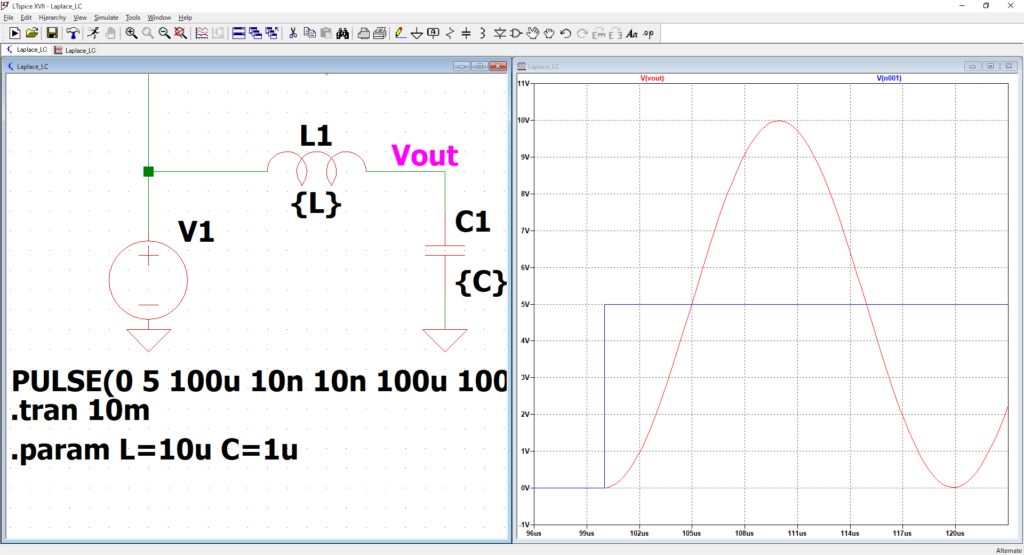
動作はこんな感じ。
伝達関数を計算する
さっきと同様です。伝達関数=出力/入力を目指します。
まずLとCを周波数領域へ持っていきます。L->sL、C->1/sCとなります。
つまりこう↓です。
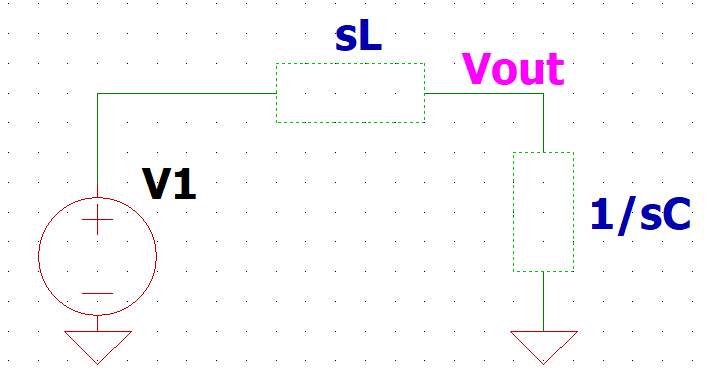
これまた同じようにVoutはV1をsLと1/sCで分圧した値になるので
$$V_{out}=\frac{\frac{1}{sC}}{sL+\frac{1}{sC}}*V1$$
分子分母にsCを掛けます。
$$V_{out}=\frac{1}{1+s^2LC}*V1$$
V1を移項します。
$$G(s)=\frac{V_{out}}{V1}=\frac{1}{1+s^2LC}$$
はいこれでOKです。
伝達関数記入と動作確認
以下のように記述しました。
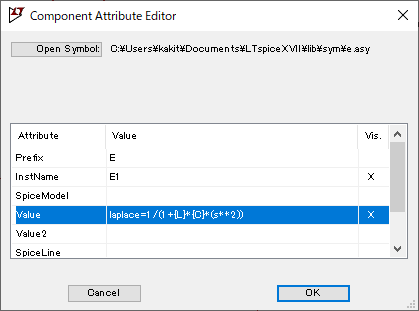
LTspiceで2乗は”**”です。
そして動作確認です。↓
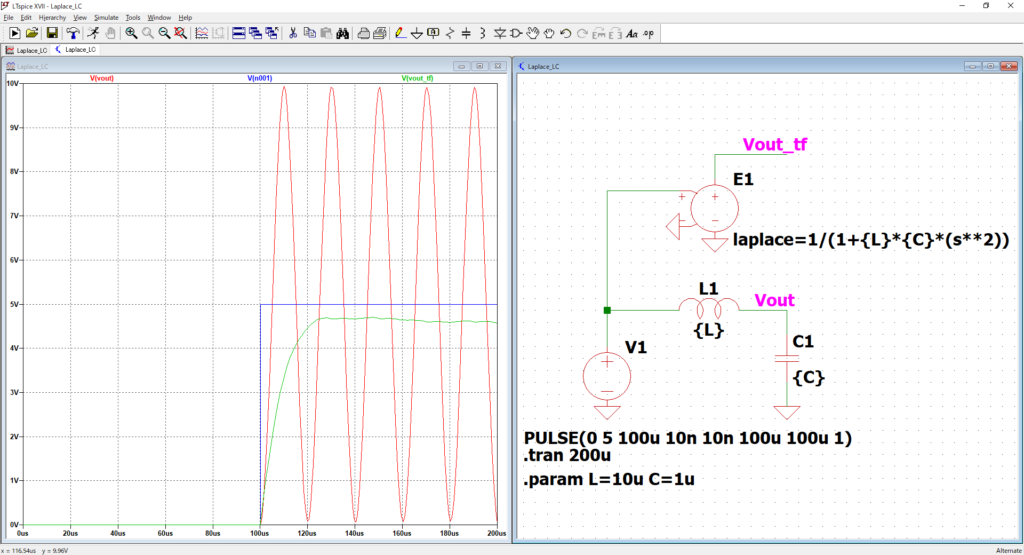
ん~合わないですね。緑が伝達関数です。
なぜかを調べるとこちらのサイトに記載がありました。
どうやら振動するものや2次以上の伝達関数の計算は怪しいようです。
ちょっと残念ですね。
まとめ
LTspiceで伝達関数を表現する方法を紹介しました。
「e」にLaplace=~と記述すれば、良いです。
ただ、2次以上は計算が微妙なので、実用はできないですかねぇ~。。。
はい。以上です。最後までお読みいただきありがとうございました。

