みなさま、お疲れ様です。
今回はPFCコンバータの出力コンデンサの話です。
PFCコンバータの出力には、大容量の平滑コンデンサが配置されます。このコンデンサの容量値を計算するときに以下の2式が出てきます。(参考文献の15ページ)
$$\small{
C_o = \frac{2 P_{out} t_{hold}}{V_{o}^2 – V_{omin}^2} \\
C_o = \frac{P_{out}}{2 \pi f_{line} \Delta V_{ripple}V_o}
}$$
上式がホールドアップ時間から容量値を計算する式で、下式は出力リップル電圧から容量値を計算する式です。
この記事では、なぜこの式で計算できるのか?を解説したいと思います。
ホールドアップ時間から容量を算出する方法
ホールドアップとは
AC入力が一時的に途絶えても、PFC出力(DCバス電圧)を一定時間維持する必要があります。
この「電源断から出力が許容電圧まで下がるまでの時間」を ホールドアップ時間(Hold-up time) と呼びます。
つまり、出力コンデンサに蓄えた電荷が放電しながら負荷を支える時間です。
計算式の導出方法_エネルギーの収支で考える
コンデンサに蓄えられるエネルギーは、
$$\small{
E = \frac{1}{2} C V^2
}$$
電源が遮断されてからホールドアップ時間 ( thold ) の間に、
出力電力 ( Pout ) が負荷に供給されるとすると、
その間に消費されるエネルギーは ( Pout×thold ) です。
したがって、電圧が初期値 ( Vo ) から許容値 ( Vomin ) に低下する間に放出されるエネルギーは:
$$\small{
\frac{1}{2}C_o(V_o^2 – V_{omin}^2) = P_{out} t_{hold}
}$$
ここからCoについてを解くと、
$$
\small{C_o = \frac{2 P_{out} t_{hold}}{V_o^2 – V_{omin}^2}}
$$
というようにエネルギーから考えるとホールドアップ時間から容量値を計算する式が導かれます。
出力リップル電圧から容量を算出する方法
リップル発生のメカニズム
PFCコンバータの出力電圧には、ACライン周波数の2倍成分(100 Hzまたは120 Hz)のリップルが含まれます。これは整流後の電圧が2倍周波数で脈動するためです。
出力コンデンサはこのリップル電流を吸収・放出して、出力電圧を平滑化します。
計算式の導出方法_Cのインピーダンス×電流で考える
コンデンサのインピーダンスをZcとして、コンデンサ電流をIrmsとすると、リップル電圧ΔVrippleは
$$\small{
\Delta V_{ripple} = Z_c I_{rms}
}$$
となります。オームの法則ですね。Zc=1/ωCoですので、
$$\small{
\Delta V_{ripple} = \frac{I_{rms}}{ωCo} \\
\Delta V_{ripple} = \frac{I_{rms}}{2 \pi f_{2line} C_o}
}$$
f2lineは系統の周波数の2倍です。
1周期あたりに負荷電力をPout、出力電力をVoとすると
$$\small{
P_{out} = V_o I_{rms}\\
C_o = \frac{P_{out}}{2 \pi f_{2line} \Delta V_{ripple} V_o}
}$$
といったように出力リップル電圧から容量値を計算する式が導出されます。
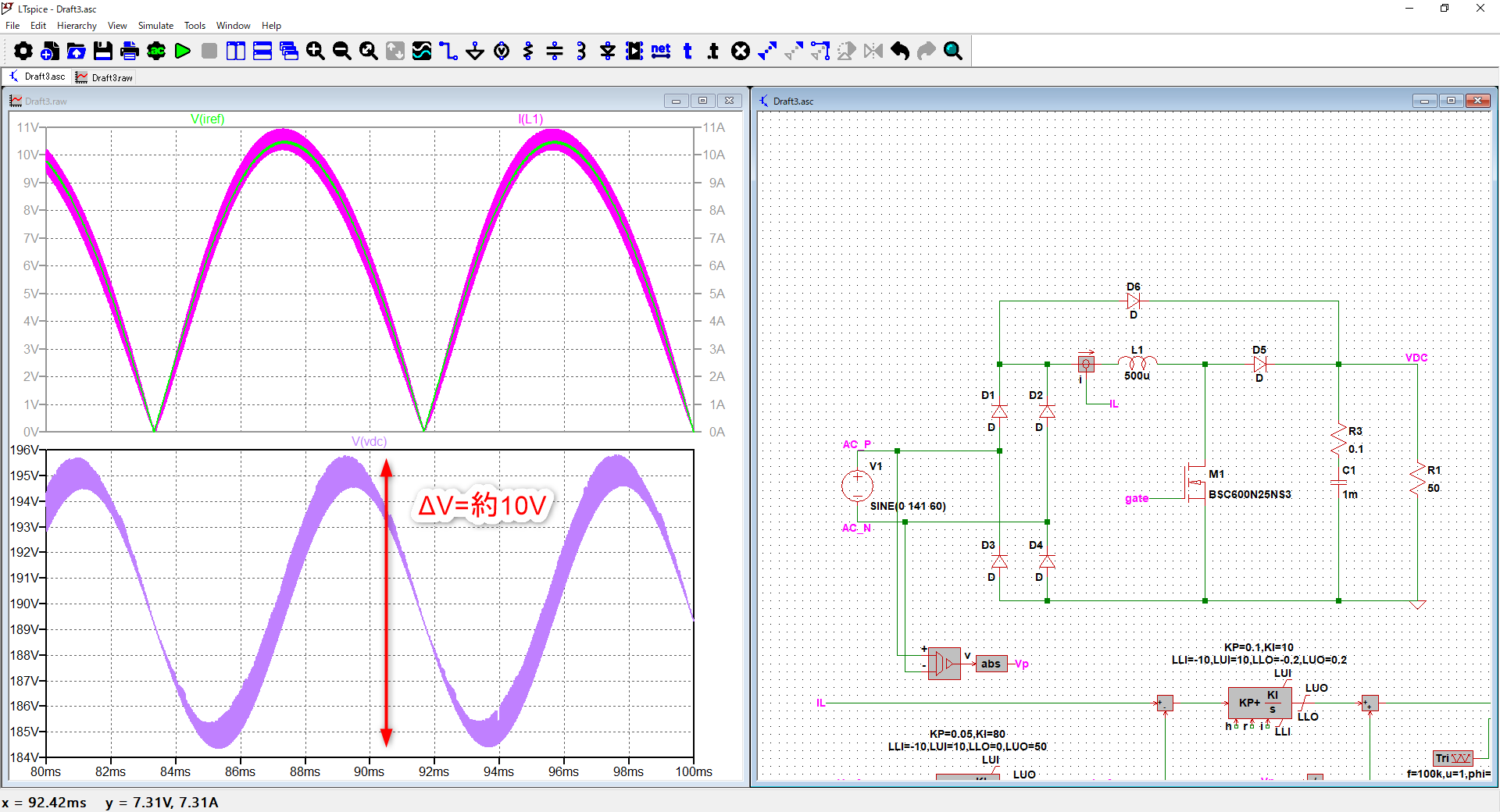
試しにシミュレーションで確認してみる
出力リップル電圧は試しに計算してシミュレーションで計算結果が合うかを見てみましょう。
計算条件は下表で計算してみます。
| パラメータ | 値 |
|---|---|
| Vout | 200V |
| f_2line | 120Hz |
| Co | 1mH |
| Pout | 800W |
$$\small{
\Delta V_{ripple} = \frac{P_{out}}{2 \pi f_{2line} C_o V_o}\\
=\frac{800W}{2 \pi 120 1m 200}≒5.3V
}$$
ということでリップル電圧は5.3Vです。さて、シミュレーション結果です。
左下の波形が出力電圧です。
計算、合わないです。なぜでしょうか。そもそもQ=CVとかで考えるべきなのかもですね。
ΔV=∫i(t)dt/Cみたいにして、計算するという感じで。
いまさら大変なので本記事は終わります。最後までお読みいただいたのに、なんかすみません。