みなさま、お疲れ様です。
本記事は物理の話です。自己インダクタンスと相互インダクタンスは何か?について解説します。
自己インダクタンス?相互インダクタンス?何ですかそれ?
高校物理の授業は寝てました。
というくらい人に向けて解説してみようと思います。
自己インダクタンスとは
自己インダクタンスはLですね。よく見るコイルの式に出てくるLです。
$$\small{
V=L\frac{Δi}{Δt}
}$$
この式を言葉にするならば、「Δiの電流をΔtの時間流すとL倍した電圧が生じる。」って感じです。
ちょっと式を変えて
$$\small{
Δi=\frac{V}{L}Δt
}$$
この式も言葉にするならば、「電圧VをΔtの時間かけると1/Lかけた電流分増加する。」って感じです。
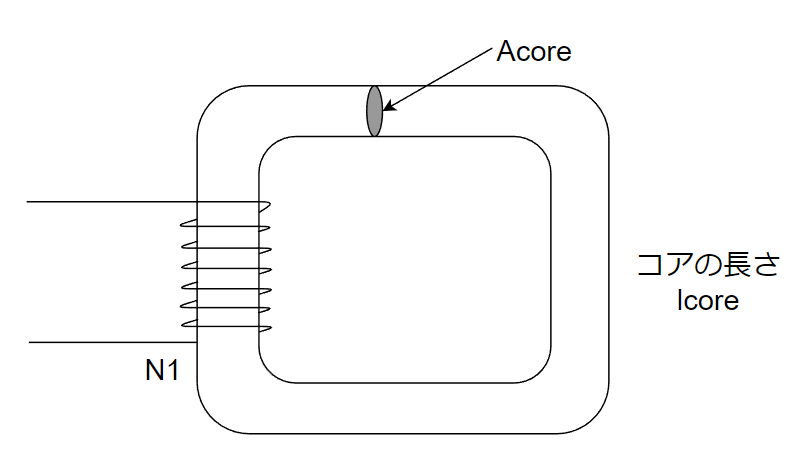
このLはコイルの形状や鉄心の種類によって決まります。以下の式で決まります。
$$
L=N^2\frac{μ_0μ_kA_{core}}{l_{core}}
$$
μ0:真空の透磁率(定数)、μk:コアの透磁率(定数)、lcore:コアの長さ、Acore:コアの断面積、N:巻き線数
相互インダクタンスとは
問題はこっちです。
まずは相互インダクタンスを考えるときは以下のようなコアを共通に持つ複数巻き線を考えます。

n1の方のインダクタに電流Δi1をΔt時間流した時を考えます。すると磁束Φ1が生じてそれがn2を貫きます。
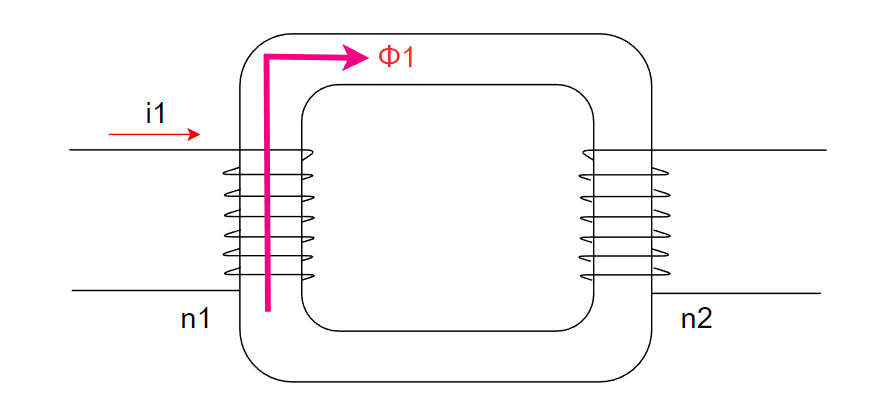
このΦ1は以下の式で計算できます。
$$\small{
ΔΦ1=\frac{N_1μA_{core}}{l_{core}}Δi_1
}$$
漏れ磁束を考えない理想的な場合を考えるとΔΦ1はそのままn2コイルを貫きます。
そのときの誘導起電力は
$$\small{
V2=N_2\frac{ΔΦ}{Δt}
}$$
このΔΦはΔΦ1なので
$$\small{
V2=N_2\frac{\frac{N_1μA_{core}}{l_{core}}Δi_1}{Δt}\\
V2=\frac{N_1N_2μA_{core}}{l_{core}}\frac{Δi_1}{Δt}\\
}$$
となります。この式前半を相互インダクタンスと言います。
$$\small{
M=\frac{N_1N_2μA_{core}}{l_{core}}
}$$
つまり
$$\small{
V2=M\frac{Δi_1}{Δt}
}$$
この相互インダクタンスは「1次コイルに電流変化させるとM倍されて2次側に電圧が生じる。」って意味です。
この式もちょっと変形すると
$$\small{
Δi_1=\frac{V2}{M}Δt
}$$
言葉にするならば、「2次コイルにV2掛けられたら1次コイル電流はV2/Mで増加していきます。」って意味になります。
自己インダクタンスはコイル1に流れる電流がコイル1に起電圧を発生させます。
相互インダクタンスはコイル1に流れる電流がコイル2に起電圧を発生させます。
って感じに覚えるといいかなと思います。
ちなみに相互インダクタンスMの式と自己インダクタンスの式を並べると
$$\small{
M=\frac{N_1N_2μA_{core}}{l_{core}}
}$$
$$\small{
L_1=N_1^2\frac{μA_{core}}{l_{core}}
}$$
$$\small{
L_2=N_2^2\frac{μA_{core}}{l_{core}}
}$$
以下の関係があることが分かります。
$$\small{
M=\sqrt{L_1L_2}
}$$
実際は磁束の漏れがあるので、結合係数を使用して
$$\small{
M=k\sqrt{L_1L_2}
}$$
と表現します。
もしL1=L2なら
$$\small{
M=k\sqrt{L^2}\\
M=kL
}$$
ってなりますね。
つまりL1=L2において、漏れインダクタンスLlkは
$$\small{
Llk=L-M
}$$
ですね。
はい、そんな感じで本記事は終わります。
誰かの参考になれば幸いです。最後までお読みいただきありがとうございました!!

