【電源回路】フルブリッジ型LLCコンバータの励磁インダクタンス最大値はなぜLm≦TTdead/16Cossなのか？

みなさま、お疲れ様です。フルブリッジ型LLCコンバータを勉強する記事の3回目です。

今日はフルブリッジ型LLCコンバータの励磁インダクタンスについての話です。

まずはこちらの資料を見て下さい。この資料の式(14)にフルブリッジ型LLCコンバータの励磁インダクタンスの最大値を制約する式が出てきます。これです↓。

$$\small{
L_m≦\frac{TT_{dead}}{16C_{oss}}
}$$

は？何この式？なんで励磁インダクタンスをこの値以下にしなきゃいけないの？という非常にニッチな疑問について解説します。

と悩んでいる方の参考になれば幸いです。

では始めます。

この式はターンオンするときにZVSを成立させたい！って思いから来てる

まず右脳で理解するためにイメージです。

フルブリッジLLCコンバータのQ1とQ4がONからOFFに切り替わるシーンを考えます。

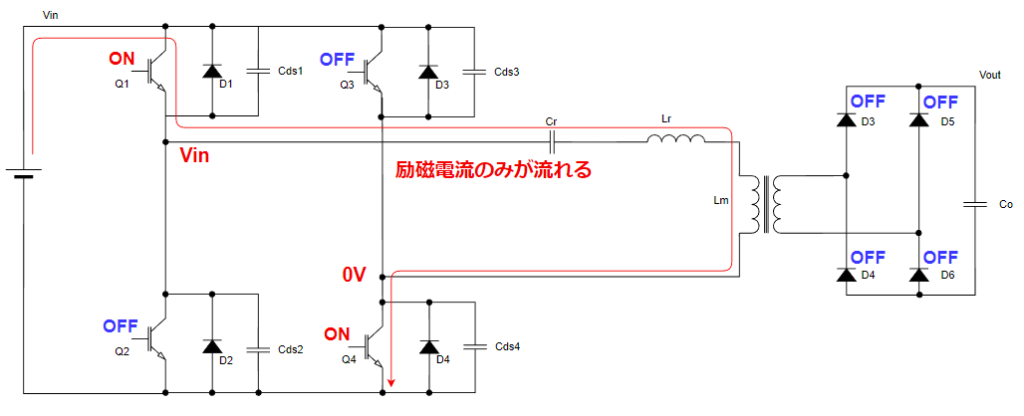
波形でいうとモード2からモード3への切り替わり時の話です↓。

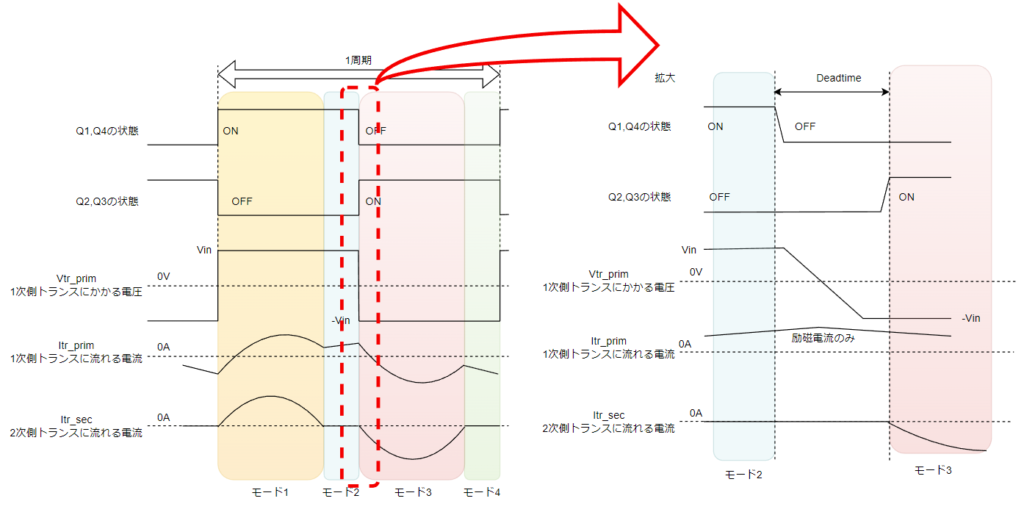
スイッチング周波数はfm～frの間で動かしていた場合、オフする前のトランス電流は励磁電流のみとなっています。

その励磁電流がスイッチの寄生容量に充放電することによって、スイッチの中間電位はじわじわと上昇していきます。

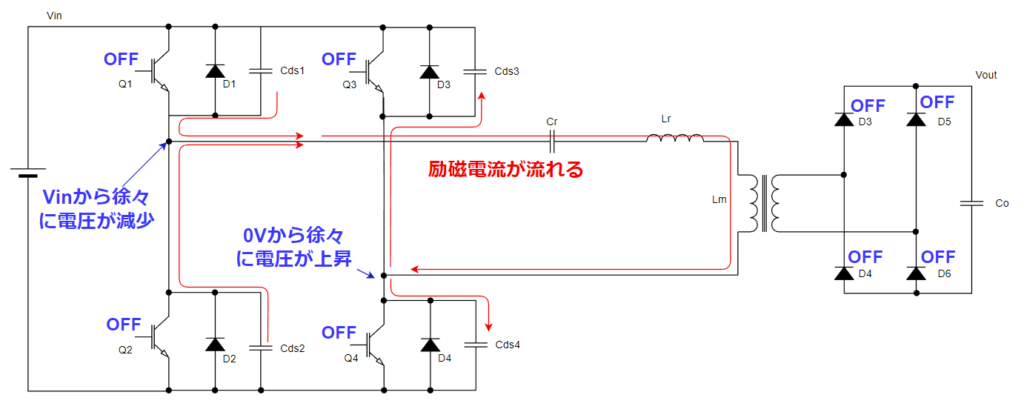
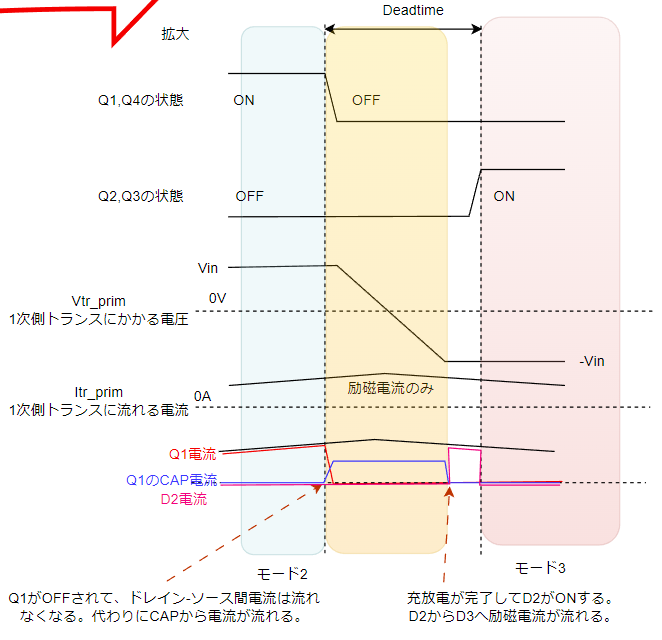
これによりスイッチがターンオフするときのZVSを成立させています。

スイッチON時は中間電位が上がり切って、ダイオードD2とD3がONしてからスイッチQ2,Q3をターンオンしますが、ここがポイントです。

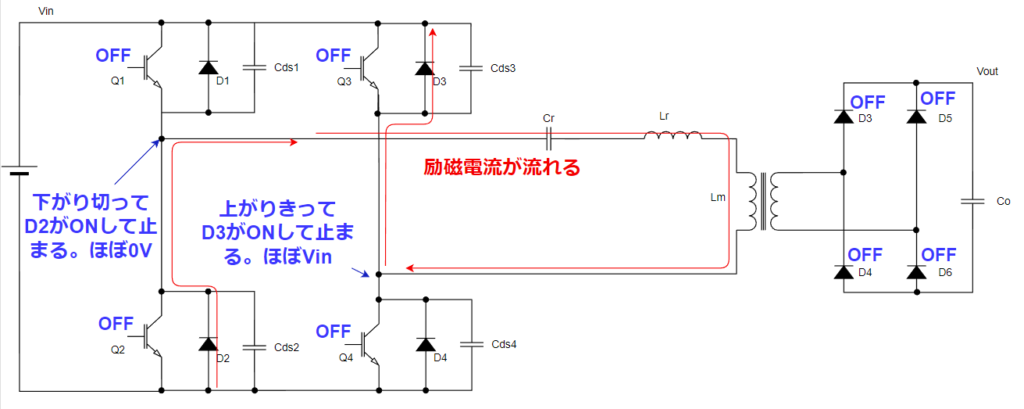
ここで励磁電流が小さすぎて、充放電時間がめっちゃ長かったらどうなるでしょうか？

つまり中間電位がめっちゃゆっくり上がっていったらどうなるでしょうか？

電圧が上がり切ってダイオードから流れだす前にスイッチQ2,Q3がターンオンします。そのすると充放電の電荷がスイッチQ2,Q3にズゴーって流れます。

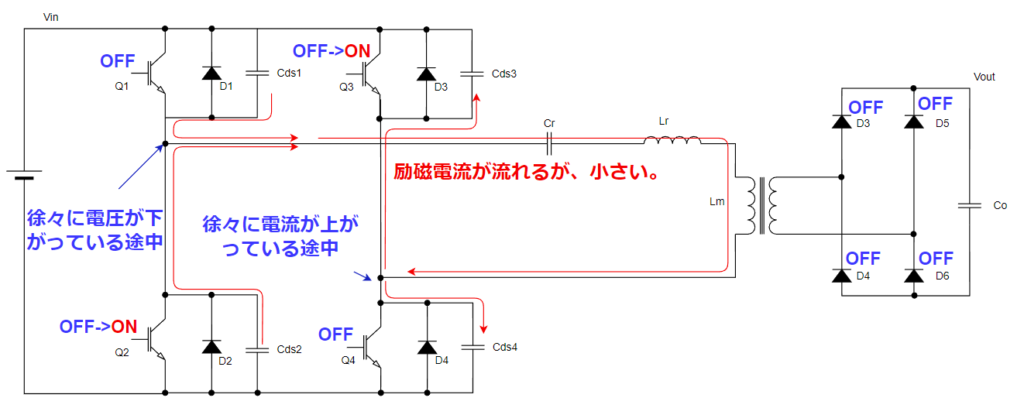
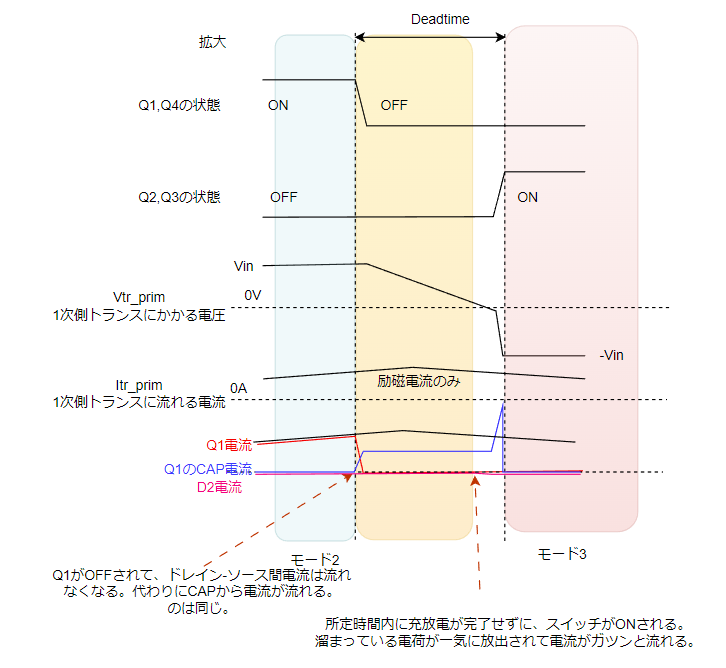
ZVS失敗です。このようにコンデンサへの充放電時間が長すぎるとZVS失敗してしまいます。

充放電時間を決めているのは単純に容量値と電流値です。(Q=CV⇔It=CVだから)

電流値は励磁電流のことです。励磁電流が小さすぎると充放電時間が長くなります。励磁電流は励磁インダクタンスが大きいと小さくなります。(V=Ldi/dtだから)

つまり、ターンオン時にZVSさせるためにはスイッチがONする前に充放電を完了させないといけない。そうなる励磁電流になるように励磁インダクタンスはある値以下にしないといけないよ！という思いが詰まっているのが

$$\small{
L_m≦\frac{TT_{dead}}{16C_{oss}}
}$$

この式なんですね。

じゃあ、この式はどうやって導出されるのかを解説します。

励磁インダクタンス最大値の式　導出過程

Q1,Q4OFF後、中間電位はGND基準からみるとVIN電圧まで上がっています。これを励磁電流で抜いていきます。

まずQ=CVの式でこの充放電時間を計算します。

次に充放電電流の励磁電流を計算します。

その結果を利用して、Lmの制約式を導出していきます。

容量への充放電時間を計算する

1次側の4つのスイッチに付いているコンデンサに励磁電流Imで充放電を行います。なので単純にコンデンサの式Q=CVから

$$\small{
I_mt=4C_{oss}V_{DS}
}$$

これをt=に整理します。

$$\small{
t=\frac{4C_{oss}V_{DS}}{I_m}
}$$

はい、これが充放電にかかる時間です。

励磁電流を計算する

励磁電流Imを計算します。励磁電流は三角波ですが、OFFする瞬間はこんな感じ↓でピーク値です。

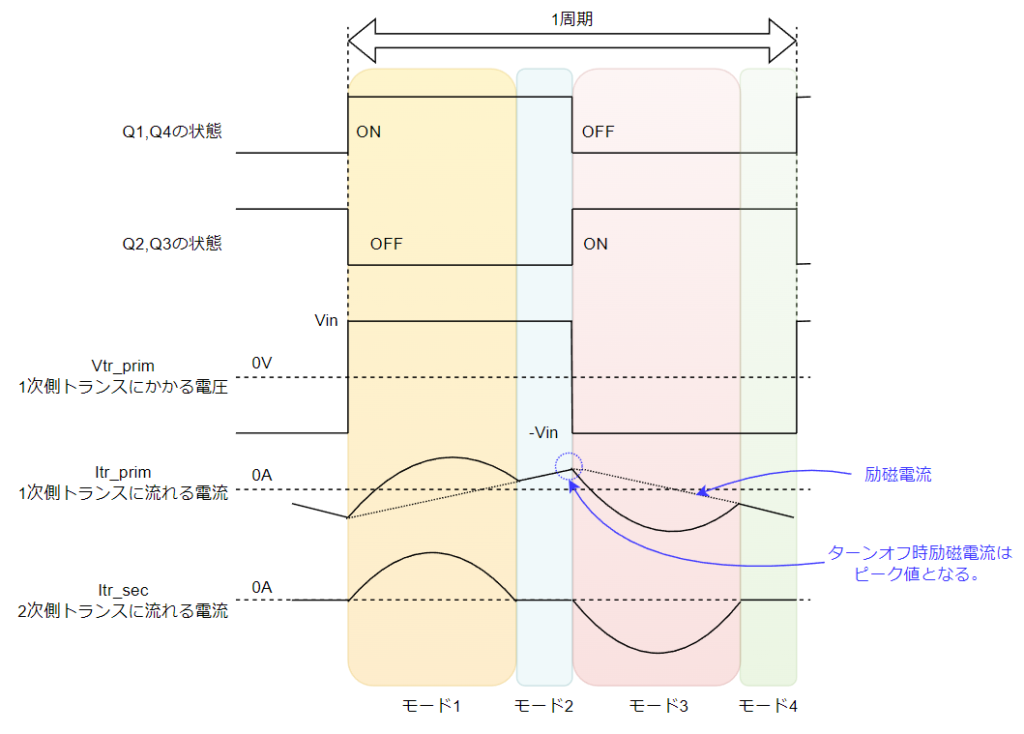
スイッチOFF/ONの切り替え時間は一瞬なので、ほぼずっとこのピーク値で電荷を引き抜きます。なので、ピーク値を計算したらいいですね。

励磁電流は一周期でこんな感じ↓なので、ピーク値はΔImの1/2です。

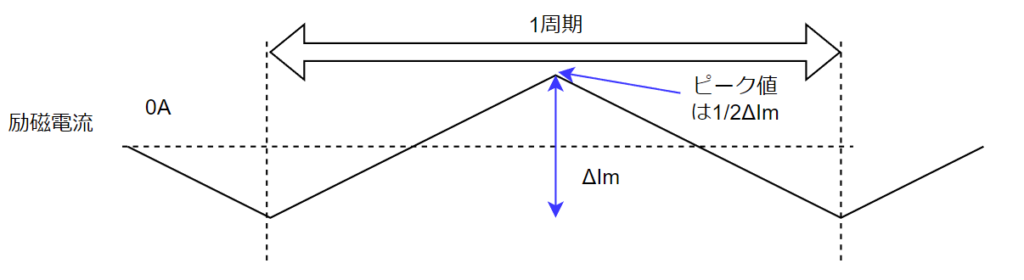
まずΔImを計算します。単純にコイルの式V=Ldi/dtから

$$\small{
V_{DS}=L_m\frac{ΔI_m}{Δt}
}$$

ΔIm=に整理します。

$$\small{
ΔI_m=\frac{V_{DS}Δt}{L_m}
}$$

この1/2が励磁電流です。

$$\small{
I_m=\frac{V_{DS}Δt}{2L_m}
}$$

はい、これが充放電電流になります。

ここでΔtはLLCコンバータのON時間です。LLCコンバータは50%Duty固定で動くので、

$$\small{
Δt=\frac{T_{sw}}{2}
}$$

となります。

励磁電流を充放電時間の式に代入する

この式↓にさっきの励磁電流を代入します。

$$\small{
t=\frac{4C_{oss}V_{DS}}{I_m}
}$$

$$\small{
t=\frac{4C_{oss}V_{DS}}{\frac{V_{DS}Δt}{2L_m}}
}$$

VDSを消して、いい感じに整理します。

$$\small{
tΔt=4C_{oss}2L_m
}$$

Δt=Tsw/2なので

$$\small{
t\frac{T_{SW}}{2}=4C_{oss}2L_m
}$$

Lm=の形に整理すると、、、

$$\small{
L_m=\frac{T_{SW}t}{16C_{oss}}
}$$

出てきましたね。充放電時間tがスイッチS2,3がONするまでの時間tdeadより小さくないといけないので、

$$\small{
L_m=\frac{T_{SW}t}{16C_{oss}}≦\frac{T_{SW}t_{dead}}{16C_{oss}}
}$$

となって、これが最初の式ですね。

はい、以上です。何かの参考になれば幸いです。

最後までお読みいただきありがとうございました！！！