みなさま、お疲れ様です。
本記事ではフライバックコンバータの動作原理を解説してみようと思います。
- フライバックコンバータの動作が分からない!!!
- 入出力電圧関係式がなんでこの式になるのか分からない!!!
という方の参考になれば幸いです。
ちなみに回路図はこんな感じですね↓。
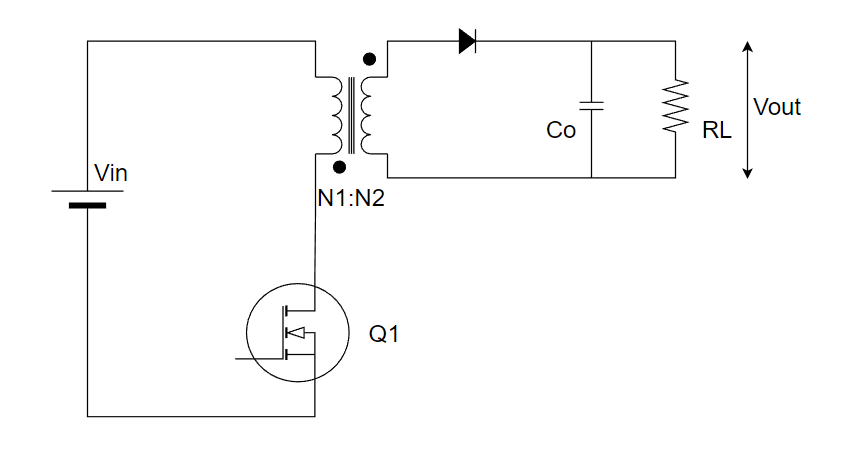
では、始めます。
2つの動作モード
動作モードは2通りです。
そもそもスイッチが1個だけなので、まぁこの2個だけです。
| モード | Q1 | 備考 |
|---|---|---|
| 1 | ON | 1次側に電流を流す。 |
| 2 | OFF | 2次側に電流を流す。 |
ちょっとややこしいのが、トランスに流れる電流が連続のときと不連続のときとで計算式が異なるってことです。
連続モード(CCM)はトランス電流が0Aのときがありません。

不連続モード(DCM)はトランス電流が0Aのときがあります。
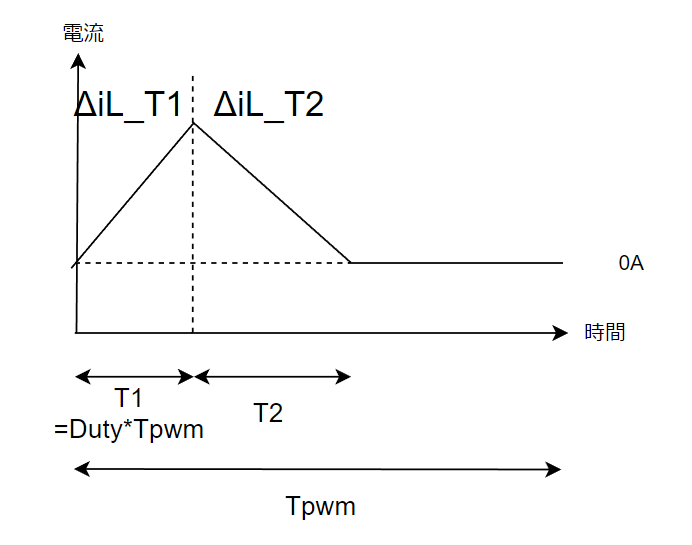
DCM(=Discontinious不連続 Current電流 Mode)です。
モード1:Q1=ONのとき
Q1がONのときはそのままトランス1次側に電流が流れます。
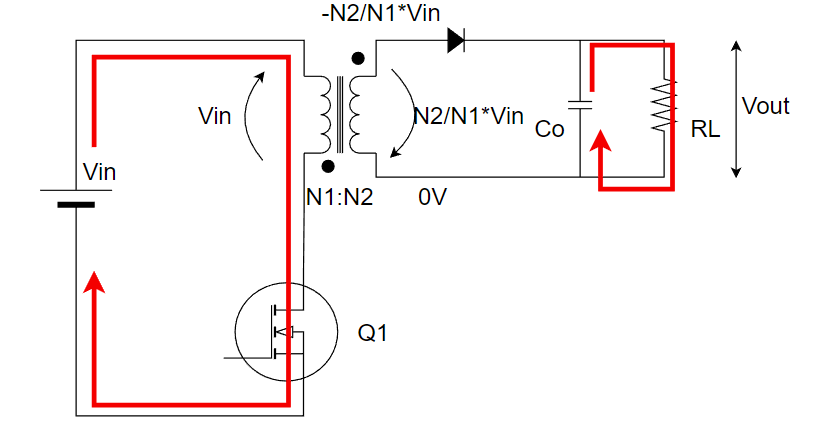
1次側トランスにVin電圧がかかるため、ファラデーの法則で2次側には巻き線比に応じた電圧が現れます。
$$\small{
V_2=\frac{N_2}{N_1}V_{in}
}$$
Vin:入力電圧[V]、V2:2次側トランス電圧、N1:1次側トランス巻き線数、N2:2次側トランス巻き線数
2次側は巻き線方向が逆なので、2次トランスの下側を0Vとするとトランスの上側電圧は-N2/N1Vinとなります。
なのでダイオードは逆バイアスされている状態のため、導通しません。出力キャパシタから電力を供給します。
1次側トランスの自己インダクタンスをLpとすると一次側トランスの電流増分は以下の式で計算できます。
$$\small{
Δi_L=\frac{V_{in}}{L_p}T_1
}$$
Lp:1次側自己インダクタンス[H]
モード2:Q1=OFFのとき
Q1がOFFすると、トランス1次側の電流は二次側に流れます。
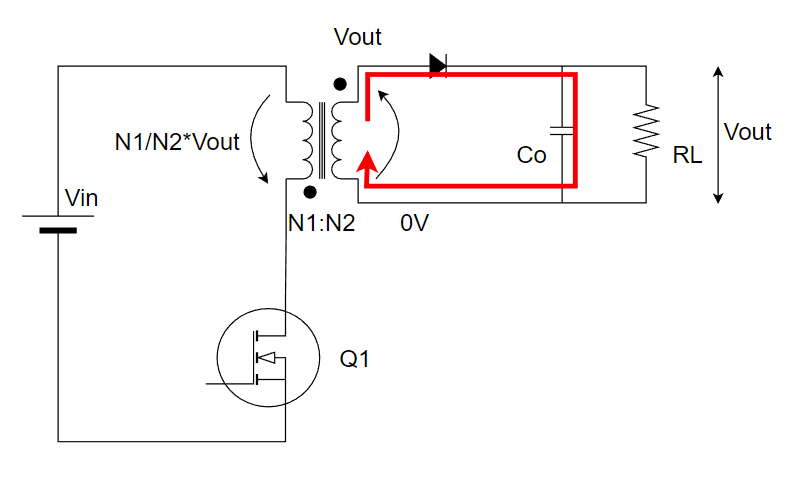
そうなると二次側のダイオードが導通して、2次側トランスにはVout電圧がかかることになります。ということはファラデーの法則で1次側トランスにはN1/N2*Voutの電圧が逆にかかっていることになります。
このときに流れている電流値を1次側に換算すると、、、
$$\small{
Δi_L=\frac{-\frac{N_1}{N_2}V_{out}}{L_p}T_2
}$$
入出力電圧関係式
CCM 連続モードのとき
電流連続モードの時は1周期で電流が連続状態にあります。

出力電圧が安定している定常状態では「ΔiL_T1とΔiL_T2が足したら0」になります。
したがって、先ほどの式を代入して解いて行きます。
$$\small{
ΔiL_{T_1}+ΔiL_{T_2}=0\\
\frac{V_{in}}{L_p}T_1+\frac{-\frac{N_1}{N_2}V_{out}}{L_p}T_2=0
}$$
1周期をTpwm、スイッチのON割合をDutyとすると、T1=DTpwm、T2=(1-D)Tpwmです。
$$\small{
\frac{V_{in}}{L_p}DT_{pwm}+\frac{-\frac{N_1}{N_2}V_{out}}{L_p}(1-D)T_{pwm}=0
}$$
TpwmやらLpやらを消します。
$$\small{
V_{in}D+-\frac{N_1}{N_2}V_{out}(1-D)=0
}$$
Vout=の式に直すと
$$\small{
V_{out}=\frac{D}{1-D}\frac{N_2}{N_1}V_{in}
}$$
これが電流連続モードCCMのときの入出力電圧関係式になります。
DCM 不連続モードのとき

不連続モードのときは「入力電力と出力電力は同じ!」という考えで式を立てます。
$$\small{
P_{in}=P_{out}
}$$
出力電力=出力電圧×出力電流です。出力電流=出力電圧/負荷抵抗です。
$$\small{
P_{in}=\frac{V_{out}^2}{R_L}
}$$
問題は入力電力です。入力電力=入力電圧×入力電流だろ。って思うかもですね。
$$\small{
V_{in}I_{in}=\frac{V_{out}^2}{R_L}
}$$
入力電圧はVinですが、入力電流Iinはいくつですか?ってなります。
この式の入力電流Iinは1周期当たりの平均値となります。平均値ってどうやって計算したらいいの?ってなります。
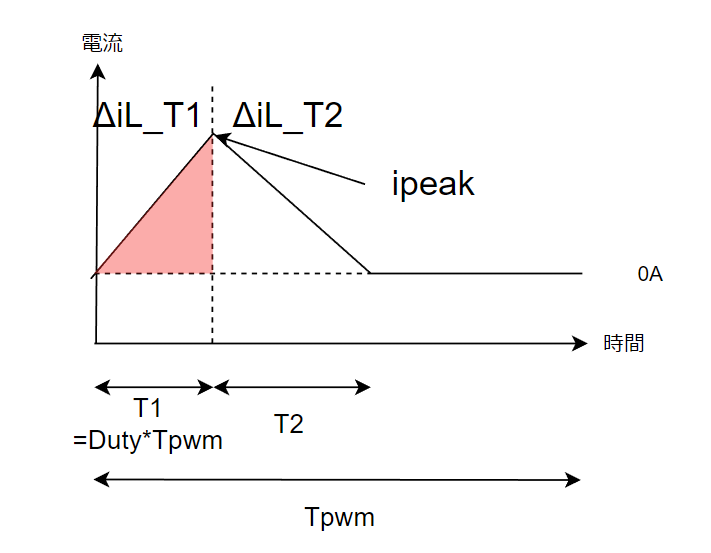
入力電荷量はこの赤のエリアになります。そのピーク値はΔiLで分かります。この面積を1周期で割ったら平均電流値になります。
したがって、
$$\small{
I_{in}=\frac{Q}{T_{pwm}}
}$$
この赤いエリアの面積は三角形の公式(底辺×高さ÷2)で計算できます。懐かしいですね。
$$\small{
I_{in}=\frac{\frac{1}{2}DT_{pmw}ipeak}{T_{pwm}}
}$$
ipeak=ΔiL_T1なので
$$\small{
I_{in}=\frac{\frac{1}{2}DT_{pmw}\frac{V_{in}}{L_p}DT_{pwm}}{T_{pwm}}
}$$
ちょっと整理します。
$$\small{
I_{in}=\frac{D^2V_{in}T_{pwm}}{2L_p}
}$$
この式をさきほどの電力の式に代入します。
$$\small{
\frac{D^2V_{in}^2T_{pwm}}{2L_p}=\frac{V_{out}^2}{R_L}\\
V_{out}^2=\frac{D^2V_{in}^2T_{pwm}R_L}{2L_p}
}$$
平方根とったらVoutが出てきますね。
$$\small{
V_{out}=\sqrt{\frac{D^2V_{in}^2T_{pwm}R_L}{2L_p}}\\
V_{out}=DV_{in}\sqrt{\frac{T_{pwm}R_L}{2L_p}}
}$$
まとめ
フライバックコンバータの入出力電圧関係式は以下の通りです。
CCM電流連続モード
$$\small{
V_{out}=\frac{D}{1-D}\frac{N_2}{N_1}V_{in}
}$$
DCM電流不連続モード
$$\small{
V_{out}=DV_{in}\sqrt{\frac{T_{pwm}R_L}{2L_p}}
}$$
はい、以上です。誰かの参考になれば幸いです。
最後までお読みいただきありがとうございました!!