皆さんお疲れ様です。
本記事ではEMCフィルターのT型フィルタの伝達関数を導出します。
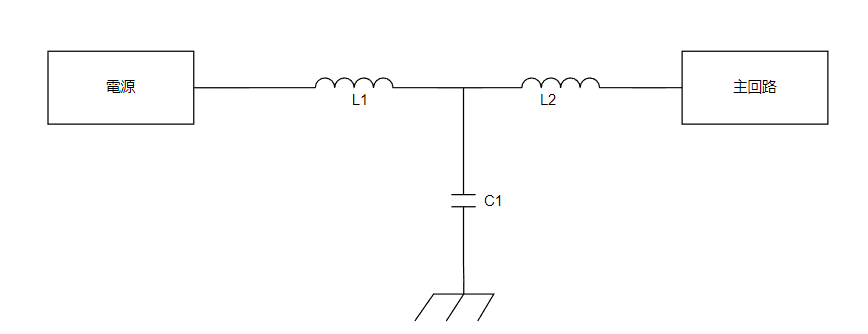
T型フィルタの周波数特性と伝達関数の導出の仕方がよくわからない
と言うお悩みを持った方に向けて、解決となると幸いです。
【結論】T型フィルタ(LCLフィルタ)の伝達関数
まず結論として伝達関数は以下の式になります。
$$\small{
\frac{I_1[s]}{V_{in}[s]}=\frac{1}{L_1C_1L_2s^3+(L_1+L_2)s}
}$$
見ての通り、3次のフィルタとなります。カットオフ周波数は以下の式になります。
$$\small{
f_c=\frac{1}{2\pi}\sqrt{\frac{L_1+L_2}{L_1C_1L_2}}
}$$
この周波数以降は-60dB/decでゲインが落ちていきます。
なんでこれになるんだよ!を以下で解説します。
T型フィルタ(LCLフィルタ)伝達関数の導出過程
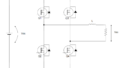
T型フィルタでノイズvin(t)が発生したとしてi1(t)がどう変動するか?を考えます。

キルヒホッフの法則やQ=CVやV=Ldi/dtを使って、式をわーっと立てます。
$$\small{
i_1(t)+i_{C1}(t)=i_2(t) \tag{1}
}$$
$$\small{
v_{L1}(t)=v_{C_1}(t) \tag{2}
}$$
$$\small{
v_{L1}(t)=L_1i_1′(t) \tag{3}
}$$
$$\small{
v_{c1}(t)=\frac{1}{C_1}\int_0^ti_{c1}(t) \tag{4}
}$$
$$\small{
v_{L2}(t)=L_2i_2′(t) \tag{5}
}$$
$$\small{
v_{L2}(t)=v_{in}(t)-v_{C_1} \tag{6}
}$$
ここから、頑張ってVinとi1の関係式を求めます。式2と3から
$$\small{
v_{C_1}(t)=L_1i_1′(t) \tag{7}
}$$
この式を式6へ代入
$$\small{
v_{L2}(t)=v_{in}(t)-L_1i_1′(t)
}$$
この式へ式5を代入
$$\small{
L_2i_2′(t)=v_{in}(t)-L_1i_1′(t)
}$$
この式に式1を代入
$$\small{
L_2(i_1′(t)+i_{C1}'(t))=v_{in}(t)-L_1i_1′(t)
}$$
この式をラプラス変換します。微分はsが付きます。
$$\small{
L_2(sI_1[s]+sI_{C1}[s])=V_{in}[s]-L_1sI_1[s] \tag{8}
}$$
Ic1が邪魔ですので、消したいです。式7に式4を代入します。
$$\small{
\frac{1}{C_1}\int_0^ti_{C_1}(t)=L_1i_1′(t)
}$$
この式をラプラス変換します。積分には1/sが付きます。
$$\small{
\frac{1}{sC_1}I_{C_1}[s]=L_1sI_1[t]
}$$
Ic1=の形に整理します。
$$\small{
I_{C_1}[s]=s^2L_1C_1I_1[s] \tag{9}
}$$
式8に式9を代入します。
$$\small{
L_2(sI_1[s]+s*s^2L_1C_1I_1[s])=V_{in}[s]-L_1sI_1[s]
}$$
これをI1[s]/Vin[s]の形に整理すると、、、
$$\small{
\frac{I_1[s]}{V_{in}[s]}=\frac{1}{L_1C_1L_2s^3+(L_1+L_2)s}
}$$
となります。
カットオフ周波数は分母=0を解いたらいいので、以下の式となります。
$$\small{
ω_C=\sqrt{\frac{L_1+L_2}{L_1C_1L_2}}
}$$
Hzに直すと、
$$\small{
f_c=\frac{1}{2\pi}\sqrt{\frac{L_1+L_2}{L_1C_1L_2}}
}$$
はい、出てきました。
本記事は以上となります。何かの参考になれば幸いです。
最後までお読みいただきありがとうございました!!