みなさま、お疲れ様です。単相インバーターの記事1回目です。
1回目:【インバーター】バイポーラSPWM制御単相インバーターの動作原理(本記事)
2回目:【インバーター】バイポーラSPWM制御単相インバーターのプラント伝達関数を計算する
3回目:【インバーター】バイポーラSPWM制御単相インバーターの動作をLTspiceで確認する
4回目:【インバーター】【インバーター】プラントGdiの周波数特性をLTspiceで確認する
5回目:【インバーター】単相インバーターの制御設計をしてみる【PR制御】
6回目:【インバーター】単相インバーターのリップル電流の求め方
本日はバイポーラSPWM制御の単相インバーターの動作原理を解説してみようと思います。
- バイポーラSPWM制御のインバーターがどう動いているのか分からない!
- なんでm(変調率)=Vac/Vdcになるの?
と悩みを持たれている方の参考になれば幸いです。
まず今回の対象の単相インバーターの回路図はこんな形をしています↓。
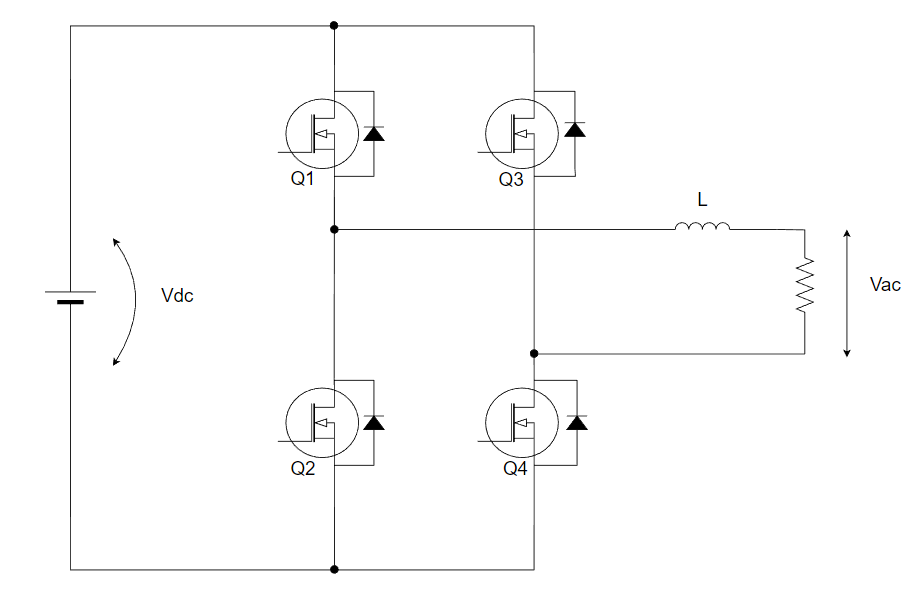
ちなみに逆方向のバイポーラSPWM制御の昇圧PWM整流器と動作は同じで、それはこちらの記事で解説しておりますので、良かったら読んでみて下さい。
【結論】Q1&Q4とQ2&Q3を交互にON/OFFする
バイポーラではQ1&Q4とQ2&Q3を交互にON/OFFします。Q1&Q4とQ2&Q3のON幅を調整することによって、出力リアクトルLにVdcと-Vdcを交互に印可しています。
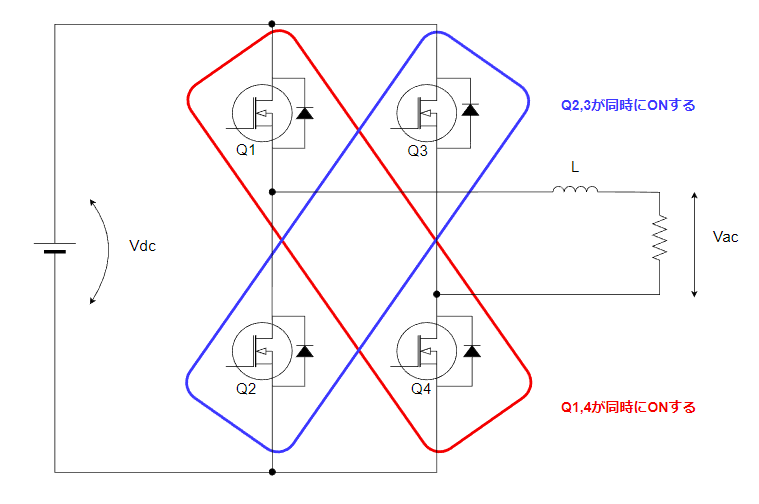
このVdc,-Vdcの印可を交互に切り替え、それぞれの印可時間を調整することによって、出力電圧を正弦波状にします。
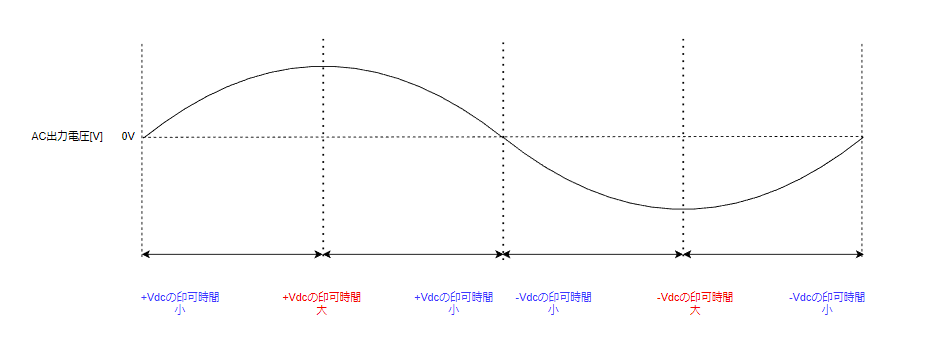
この時間を調整する方法がSPWM(正弦波PWM)制御となります。
後ほど説明しますが、三角波の搬送波と正弦波状の変調波m*sin(ωt)を比較して+Vdc,-Vdc時間を決定します。
変調波m*sin(ωt)のmは変調率というもので、DCDCコンバータでいうDuty比みたいなもんです。このmを調整することで出力電圧のピーク値を変えることが出来ます。
入出力電圧関係式は以下の式で計算することが出来ます。
$$\small{
m=\frac{V_{ac}}{V_{dc}}
}$$
Duty比って感じですが、最初はピンとこないっすね。
各動作モードがどう動くのか?とSPWMのイメージ、なぜこの入出力電圧関係式が出てくるのか?を順番に解説します。
各動作モードと電流経路
動作モードはスイッチのオンオフ状態に応じて、以下の4つのモードに分けられます。
| モード | Q1 | Q2 | Q3 | Q4 | 備考 |
|---|---|---|---|---|---|
| 1 | ON | OFF | OFF | ON | 上側半波のときの+Vdcの印可 |
| 2 | OFF | ON | ON | OFF | 上側半波のときの-Vdcの印可 |
| 3 | OFF | ON | ON | OFF | 下側半波のときの-Vdcの印可 |
| 4 | ON | OFF | OFF | ON | 下側半波のときの+Vdcの印可 |
AC入力の上側半波のときにモード1,2。下側半波のときにモード3,4となります。
モード1 上側半波の+Vdcの印可
モード1はQ1,4がオンしています。リアクトルと負荷には+Vdcが印加されています。
電流経路は以下の通りです。
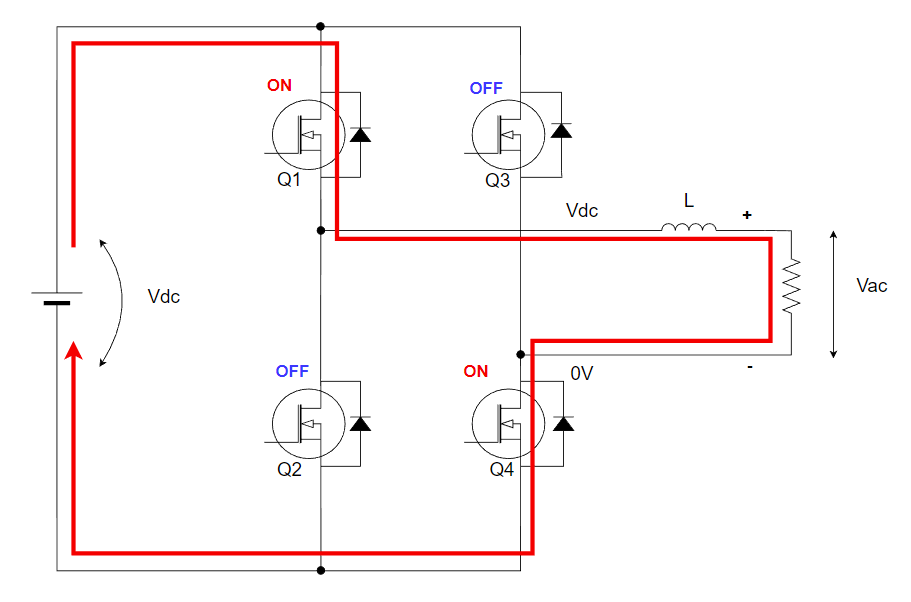
リアクトルの電流ΔILは以下の通りです。
$$\small{
ΔIL=\frac{V_{dc}-V{ac}}{L}*T_1
}$$
T1:モード1の時間
モード2 上側半波の-Vdcの印可
モード2はQ2,3がオンしています。リアクトルと負荷には-Vdcが印加されています。
電流経路は以下の通りです。
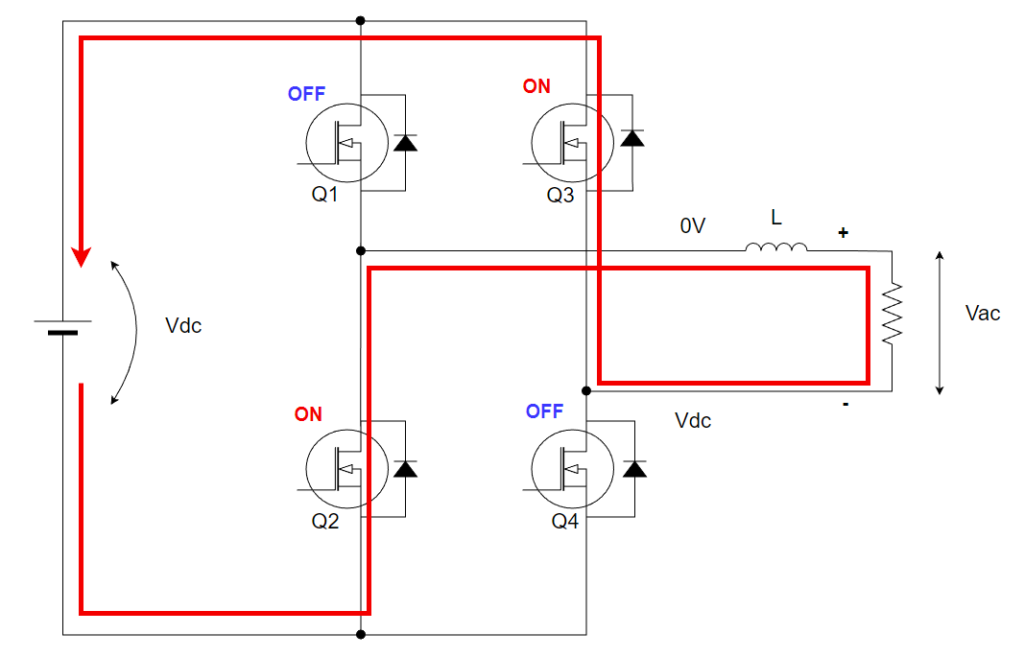
リアクトルの電流を流し続けようとする性質でモード1と同じ方向に電流が流れます。
リアクトルの電流ΔILは以下の通りです。
$$\small{
ΔIL=\frac{0-(V{ac}+V_{dc})}{L}*T_2
}$$
T2:モード2の時間
モード3 下側半波の-Vdcの印可
モード3はQ2,3がオンしています。リアクトルと負荷には-Vdcが印加されています。
電流経路は以下の通りです。
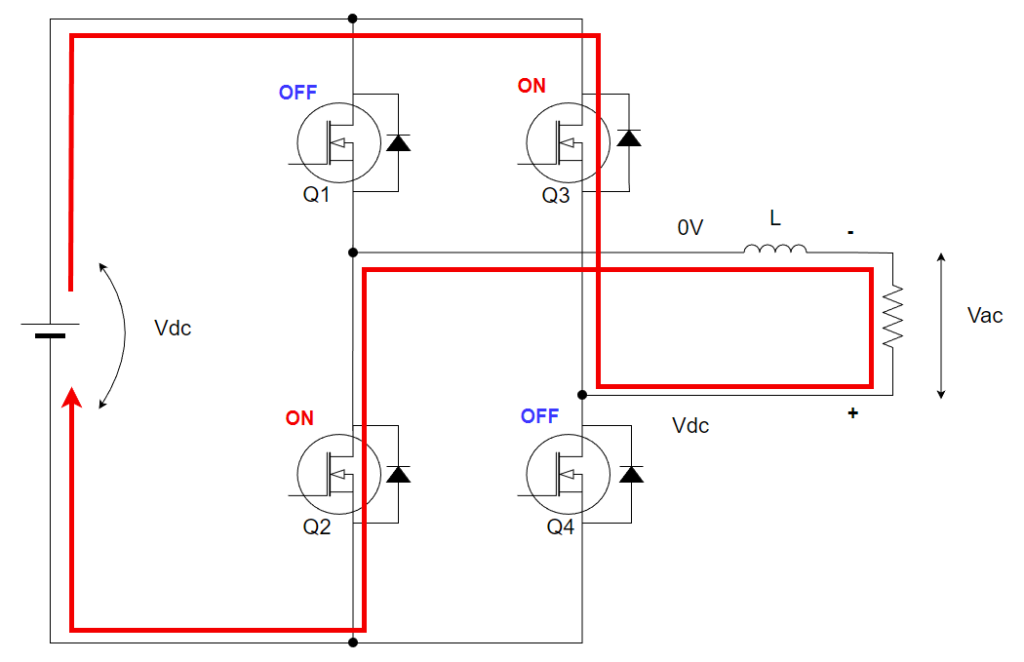
リアクトルの電流ΔILは以下の通りです。
$$\small{
ΔIL=\frac{0-(V_{dc}-V{ac})}{L}*T_3
}$$
T3:モード3の時間
モード4 下側半波の+Vdcの印可
モード3はQ1,4がオンしています。リアクトルと負荷には+Vdcが印加されています。
電流経路は以下の通りです。
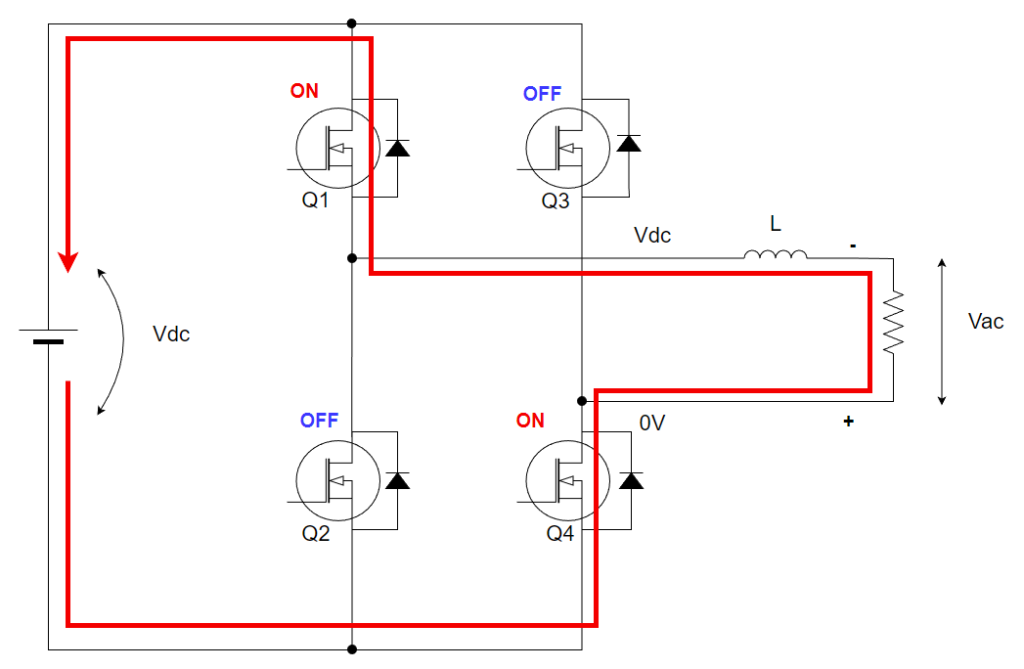
リアクトルの電流を流し続けようとする性質でモード3と同じ方向に電流が流れます。
リアクトルの電流ΔILは以下の通りです。
$$\small{
ΔIL=\frac{V_{dc}+V_{ac}}{L}*T_4
}$$
T4:モード4の時間
SPWMのイメージを解説
SPWM(正弦波PWM)制御は以下の図のような+Vdc,-Vdcの印可時間を調整することによって、出力電圧を正弦波状にする実現手段です。

具体的にはコンパレータに所望の正弦波と三角波(搬送波と言います。)を入力して、これらを比較して、ゲート信号のH/Lを決めます。
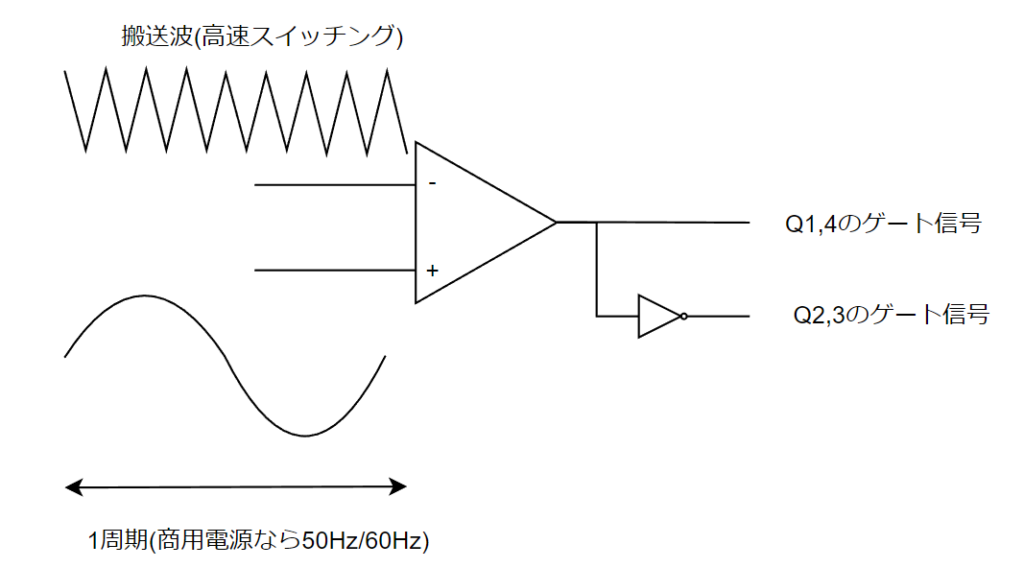
コンパレータは+入力>-入力のときはHigh出力、-入力>+入力のときはHigh出力となります。
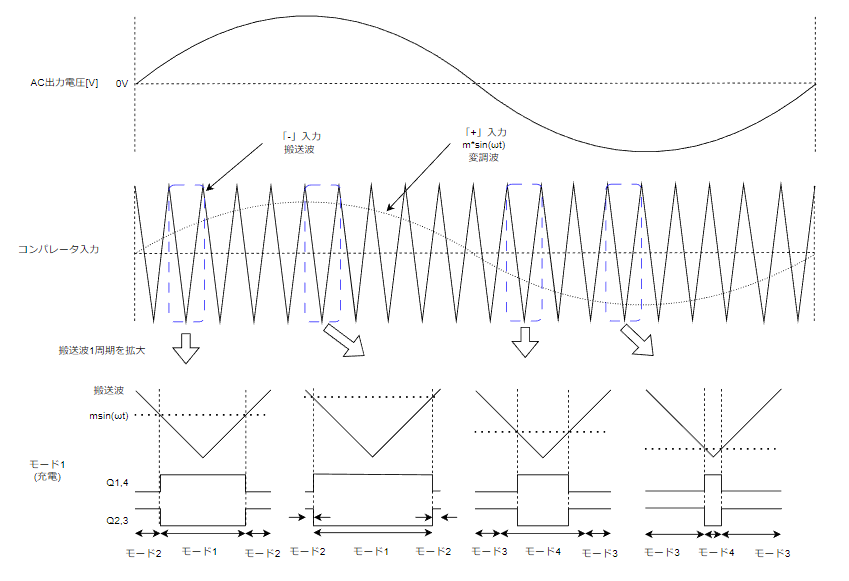
変調波のピーク付近ではモード1とモード3の時間が長くなります。上側半波では+Vdcが印可される時間が長くなるってことです。
変調波の0付近ではモード2とモード4の時間が長くなります。上側半波では+Vdcが印可される時間が短くなるってことです。
なぜm(変調率)=Vac/Vdcになるの?
なんとなく動きはわかったけど、なぜ出力電圧をコントロールする変調率mは
$$\small{
m=\frac{V_{ac}}{V_{dc}}
}$$
になるの?を解説します。
それは「正弦波(sin波)のピーク値の時点を切り取って、そのときに変調率をいくつにしたら欲しいピーク値が得られますか?」を考えたらわかります。
まずピーク値の時点を切り取って
Vacを出力したい!がやりたいことです。このときにTon,Toffの時間はいくつにしたらよいかを考えます。
単純にDCDCと同じ発想でモード1の時間(Ton)とモード2の時間(Toff)でΔILが足し合わせて0になるように時間を設定したら、出力を一定にできます。
つまり
$$\small{
\frac{V_{dc}-V_{ac}}{L}T_{on}+\frac{-(V_{dc}-V_{ac})}{L}T_{off}=0
}$$
Lを消して、Toff=Tsw-Tonなのでそれを代入して、整理すると以下の式になります。
$$\small{
\frac{T_{on}}{T_{SW}}=\frac{V_{dc}+V_{ac}}{2V_{dc}}
}$$
この式をひとまず覚えておきます。
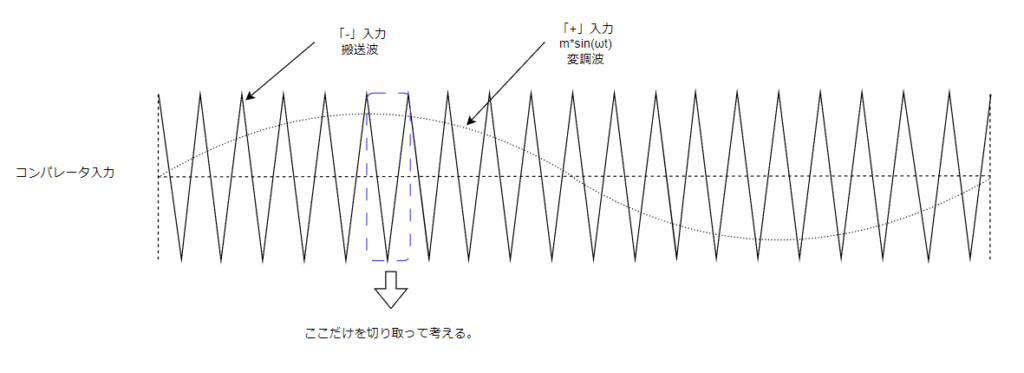
次にTonと変調率mとの関係を図形的に解きます。
搬送波1周期に限定して、変調波は一定とみなして考えると、以下の図のようになります。
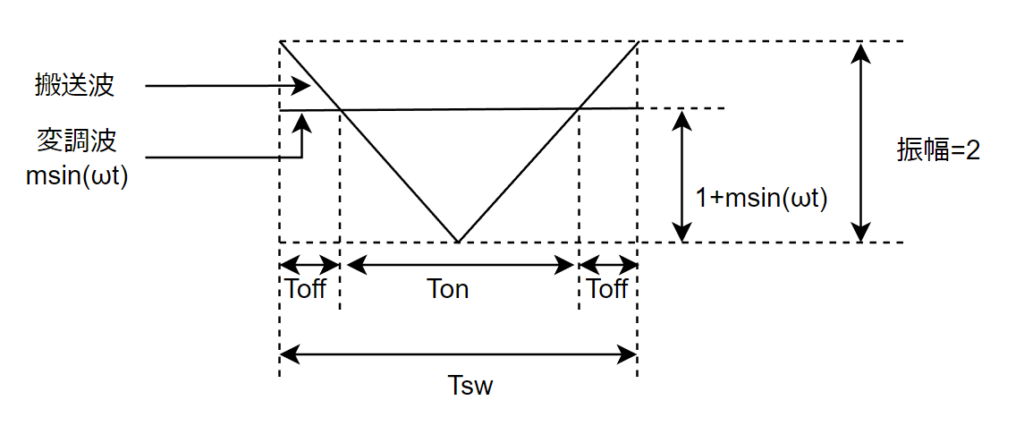
これを見ると大きい三角形とその内側に小さい三角形があります。これらは相似関係にあります。
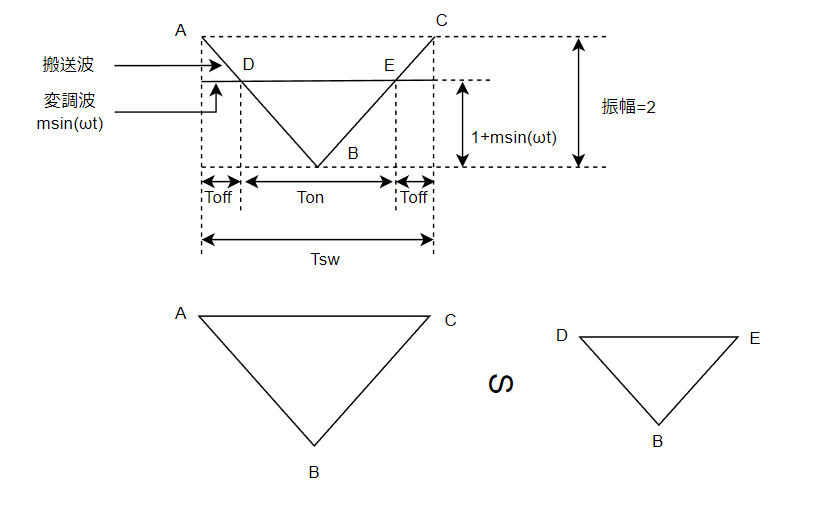
したがって、各辺の比は同じになります。つまり
$$\small{
\frac{T_{on}}{T_{SW}}=\frac{1+msin(ωt)}{2}
}$$
となります。
先ほどの式と結合します。
$$\small{
\frac{V_{dc}+V_{ac}}{2V_{dc}}=\frac{1+msin(ωt)}{2}
}$$
ピーク値はsin(ωt)=1のときなので
$$\small{
\frac{V_{dc}+V_{ac}}{2V_{dc}}=\frac{1+m}{2}
}$$
これを解くと
$$\small{
m=\frac{V_{ac}}{V_{dc}}
}$$
となります。だからm=Vac/Vdcなんですね。
はい、以上になります。
何かの参考になれば幸いです。最後までお読みいただきありがとうございました!!