PFCコンバータってむっずいですね。
初見では一体何を見て何を制御しているのか?さっぱりわかりません。しかもループ制御の設計方法って調べてもなっかなか出てこない。日本のメーカーのデータシートを読んでも書いてないし、海外メーカーのデータシート読んでも意味不明です。
ということで今回は
昇圧PFCコンバータ(CCM)の制御ってどうなってんだよ!
まずは電流ループについて考える。
という私が持っている疑問を解決できるように記事を書いていきます。
1回目:【単相PFCコンバータ】昇圧型PFCコンバータの電流ループの設計(本記事)
2回目:力率の求め方
3回目:【単相PFCコンバータ】コントローラー回路の修正と電流追従性の改善
4回目:【単相PFCコンバータ】昇圧型PFCコンバータの電圧ループの設計
ネットの海をさまよって見つけた参考資料はこことかここでございます。イングリッシュですね。あー辛い。
そもそも昇圧回路の動作
まずはさくっと昇圧回路の動作をおさらいです。以前こちらの記事で書きましたが
回路はこんな感じです。
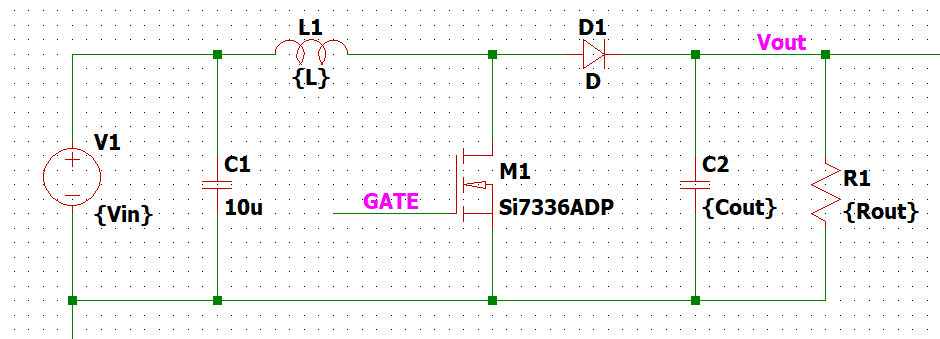
スイッチONのときは電流がこう↓流れます。
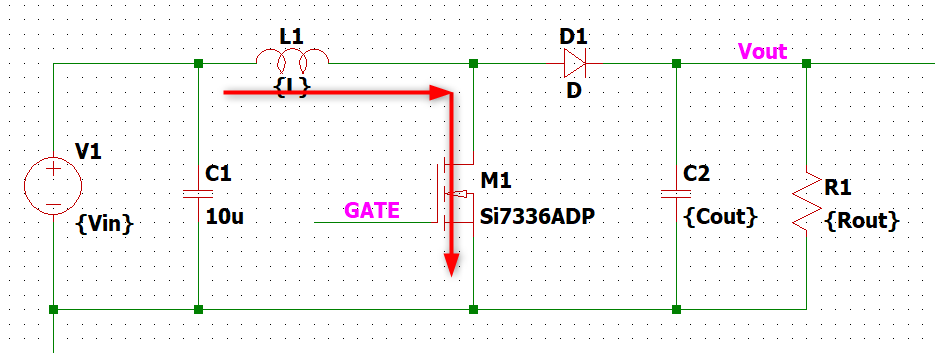
スイッチOFFのときは電流がこう↓流れます。
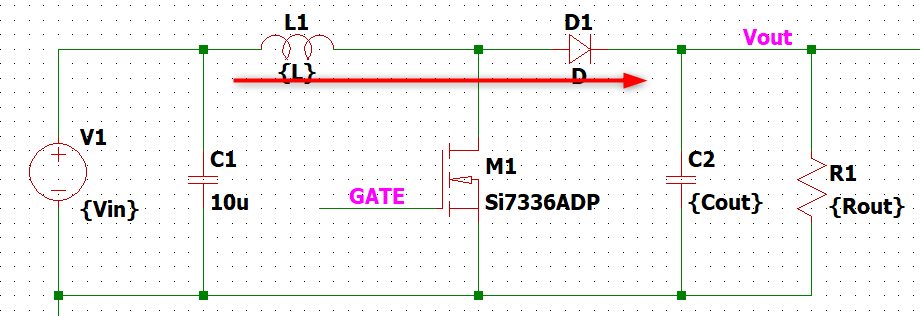
コイルの電流を流し続ける特性を活かして出力に電力を送ってます。
以下の式で出力電圧を昇圧します。
$$\small{
Vout=\frac{1}{1-Duty}Vin
}$$
ON時間が大きくなるとVoutも大きくなるって感じですね。
PFCコンバータは出力電圧と入力電流を制御している
この回路でじゃあ何を制御するんな?単純な昇圧コンバータみたいに出力電圧を制御するんか?って話ですけど、違います。
入力コイル電流と出力電圧を制御します。
は?どうやって二つ制御するんだ?って感じですが、具体的には以下のようなブロック線図で出力電圧と入力コイル電流を制御しています。
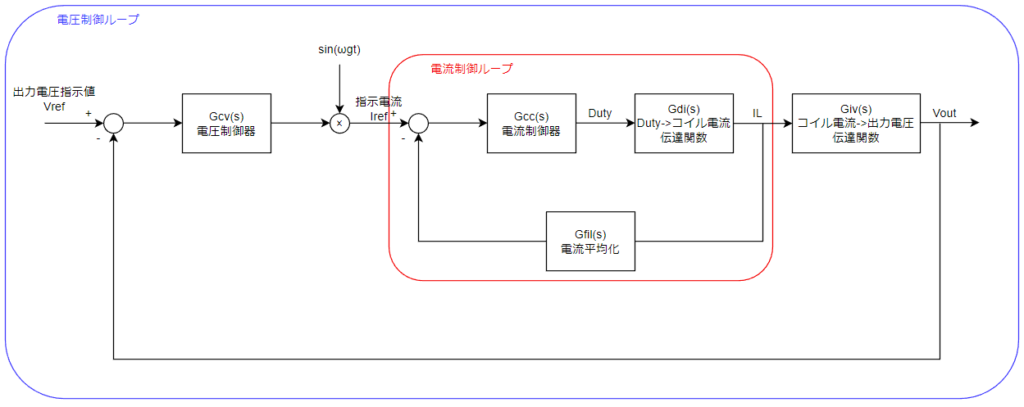
ILをフィードバックして電流が指示通りになるようにDutyで制御しつつ、出力電圧をフィードバックしてILのsin波形の高さを調整して、出力電圧が極力一定になるようにしているイメージです。
sin(ωgt)は入力のAC電源の周波数です。60Hz/50Hzですね。厳密にいえば|sin(ωgt)|ですね。これで指示電流を山なりの波形にして入力電流をsin波形にして力率を改善してぇよっていうのがPFCコンバータのやりたいことです。
電流を早く(数kHz)で制御して、出力電圧をゆっくり(数Hz)で制御します。
今回は赤枠内の電流ループのみを考えてみます。つまり、指示電流に応じてILが追随するようにするにはどうしたらいいか?を考えます。
電流制御ループの設計
電流ループの制御もふつーに電圧制御設計と発想は同じです。
伝達関数を計算して、オープンループの周波数特性で位相余裕度が確保できるようにする。というのが基本方針です。
色々資料を読んでると2pole1zero補償器を入れるって資料とP制御のみでいけるって資料がありました。
正直P制御のみで行けるって資料がよく理解できなかったので今回は2pole1zero補償器で制御を考えます。
プラント伝達関数と周波数特性
まずはDutyの変化に対するILの変化量を表す伝達関数です。
これも色々資料を読んでると抵抗負荷のときと一定電力負荷のときの伝達関数が出てきました。
まずは抵抗負荷の場合、Dutyに対する電流の伝達関数は以下の式で表されます。
$$\small{
G_{di-R}(s)=\frac{2V_{rms}}{RD’^3}\frac{1+\frac{sCR}{2}}{Δ(s)}\\
Δ(s)=\frac{s^2}{ω_o^2}+\frac{s}{ω_oQ_o}+1\\
ω_o=\frac{D’}{\sqrt{LC}},Q_o=\frac{R}{Lω_o}
}$$
Vrms:入力交流電圧実効値[V]、R:負荷抵抗[Ω]、C:出力コンデンサ容量値[F]、D’:1-D、D:スイッチングON DUTY[%] (Vout-Vin/Vout)、L:コイルのインダクタンス値
定電力負荷の場合は以下の式で表されます。
$$\small{
G_{di-CP}(s)=\frac{V_{rms}}{D’^3}\frac{sC}{Δ(s)}\\
Δ(s)=\frac{s^2}{ω_o^2}+\frac{s}{ω_oQ_o}+1\\
}$$
この式の導出には状態平均化法で状態空間モデルを書いて、しこしこ解いて行ったら出てきます。
でも、偉い人が解いているんだから、それを使わしてもらえばいいじゃんか。そう思っています。
今回の記事はこの論文から式を持ってきてます。
さてこの2つの伝達関数ですが、実は周波数特性がほぼ同じです。低域に零点があり、LCの2次共振ポールがある感じです。試しにこの2式の周波数特性を計算してみます。
まずPspice for TIで伝達関数ブロックを書いて
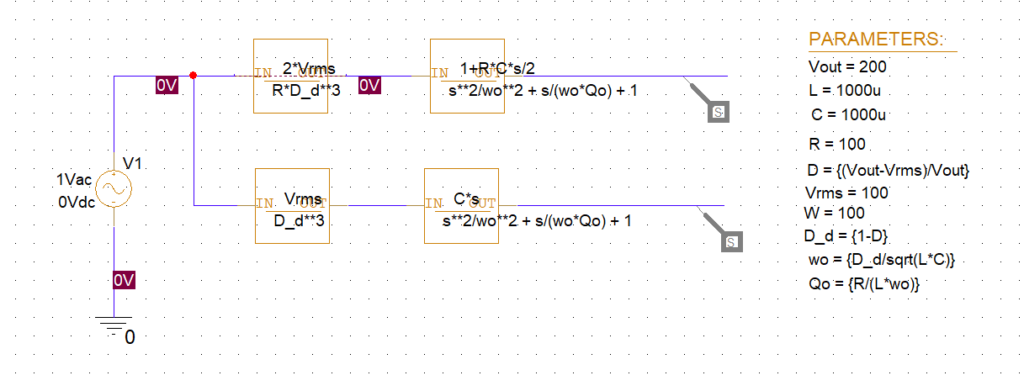
下:定電力負荷
シミュレーション結果が以下の通り。
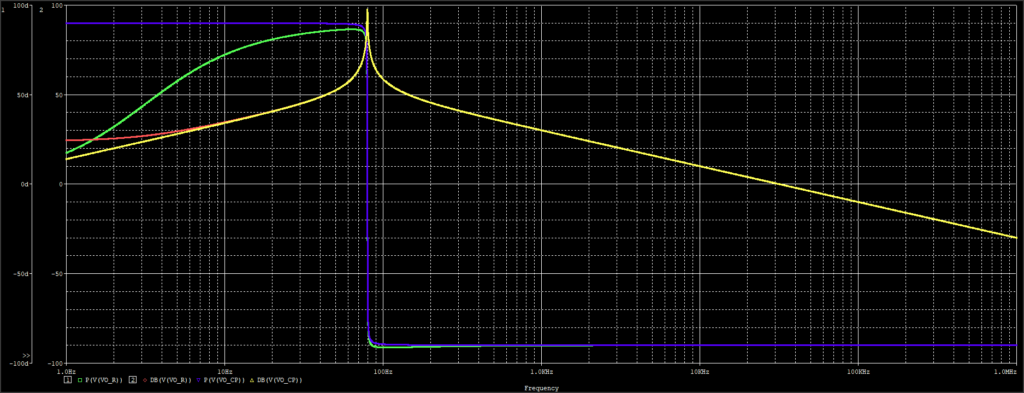
定電力負荷のゲイン(青)と位相(黄)
条件:L=1000uH、C=1000uF、Vo=200V、R=100V(=100W出力)、Vrms=100Vac
LC共振周波数以降はほぼ一緒です。なので、抵抗負荷だの定電力負荷だのと議論するのは些末な問題です。
また、電流ループのゼロクロス周波数はLC共振周波数より高い位置(数kHz)で取るから、低周波数領域邪魔だよね。ってことで近似したら以下の1次ポールの形で表されます。
$$\small{
G_{di-app}(s)=\frac{Vo}{sL}
}$$
え?マジで?こんな単純な式で本当に近似できるのかよ?と私は思ったので、試しに周波数特性を見てみます。同様に伝達関数ブロックを書いて
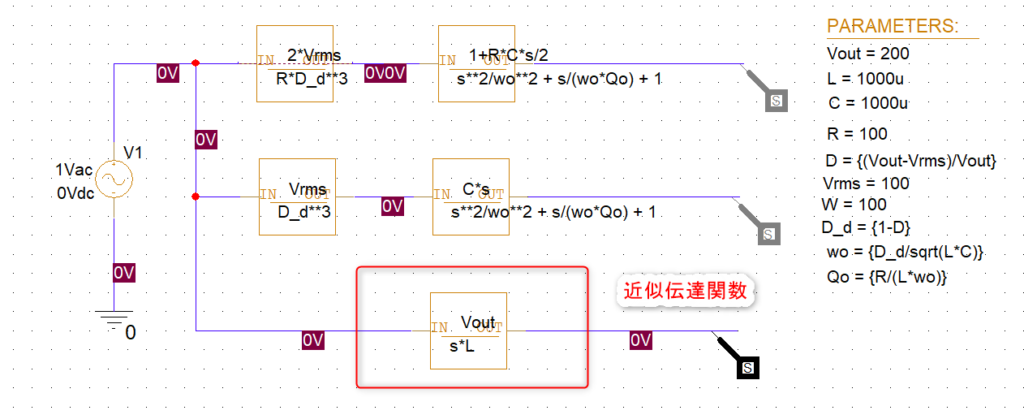
シミュレーション結果が以下です。
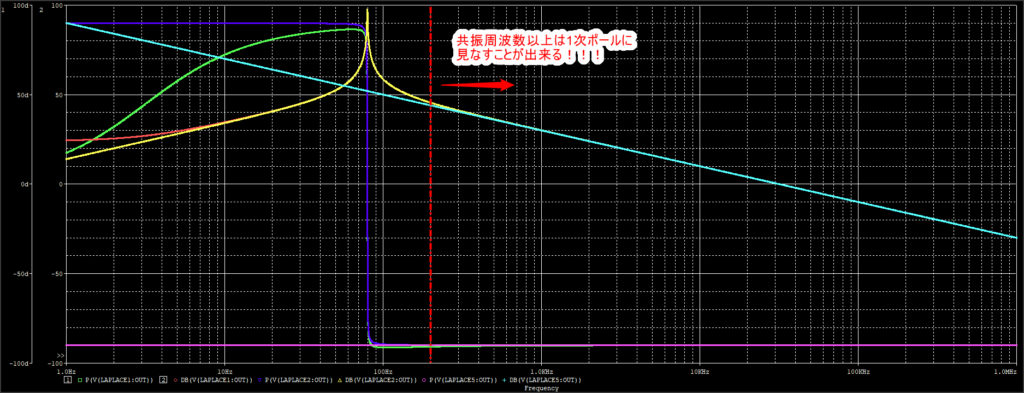
定電力負荷のゲイン(青)と位相(黄)
近似のゲイン(水色)と位相(紫)
本当に一致してますね。
はい。まぁこれらをもとに電流ループの制御設計したらいいですね。
電流平均化フィルタ
電流フィードバックするときにコイルに流れる電流のリップル成分を除去するためのGfil(s)があります。1次のLPFと想定すると以下の式で表されます。
$$\small{
G_{fir}(s)=\frac{1}{1+\frac{s}{ω_{fil}}}
}$$
これはどこら辺に置くのか良く分かってないですが、、、スイッチング周波数付近のポールなので、まぁあんまし影響はなさそうっすね。
補償器Gcc(s)
補償器は2pole1zero補償器としました。無駄時間や電流平均化フィルタの位相遅れがあるから、PI制御器(=1pole1zero)でも行けるような気がします。実際そういう資料もありました(どれか忘れましたが)。
$$\small{
G_{cc}=\frac{ω1}{s}\frac{1+\frac{s}{ωz}}{1+\frac{s}{ωp}}
}$$
セオリーとしてはスイッチング周波数の1/10程度になるようにゼロ点ωzとDCゲインω1を設定します。
系全体の周波数特性を見ながら補償器の係数を設定
さて、さきほど出てきた伝達関数たちを繋げて周波数特性を見ながら係数を調整します。
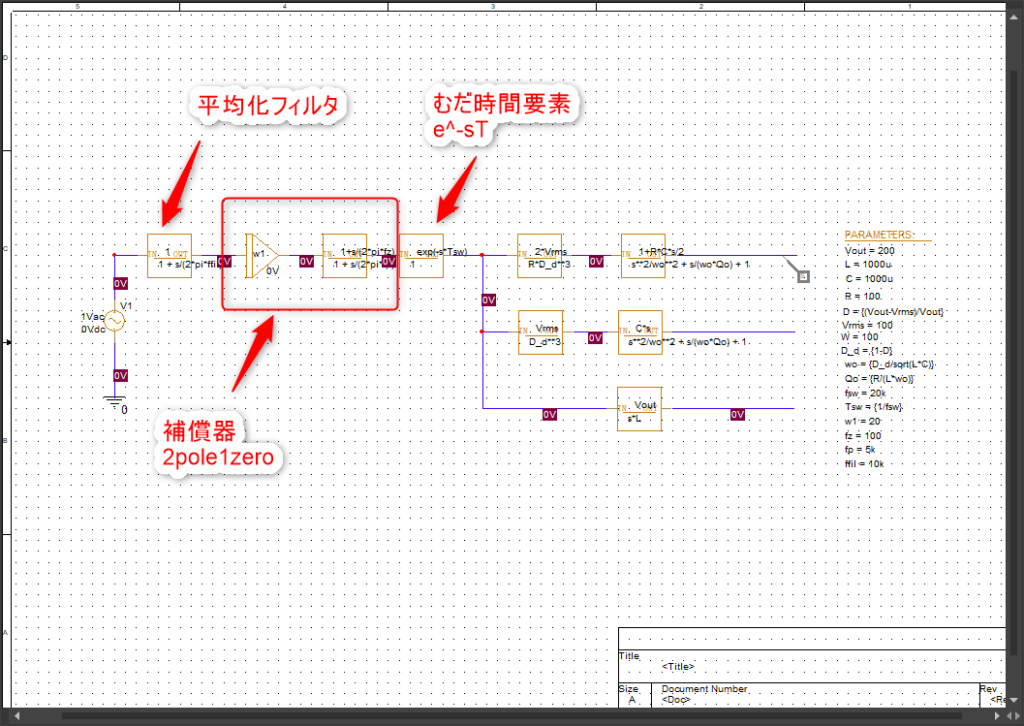
今回はスイッチング周波数=20kHz、L=1mH、C=1mFという条件で
pole周波数=5kHz、ゼロ点周波数=100Hz、DCゲインω1=20としてみました。その結果が以下の周波数特性です↓。
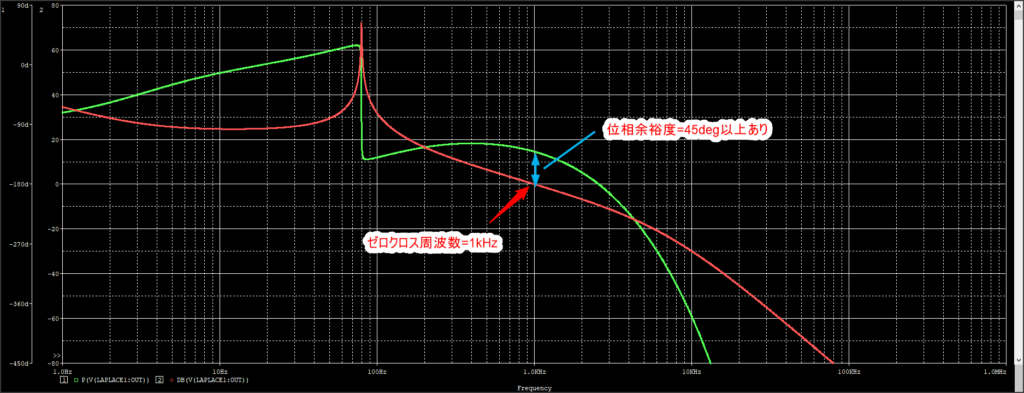
一応安定と判断できます。まぁこれでいいんかな?いったんこれでシミュレーションしてみます。
シミュレーションにて動作確認
はい、シミュレーション回路図を以下に用意しました。
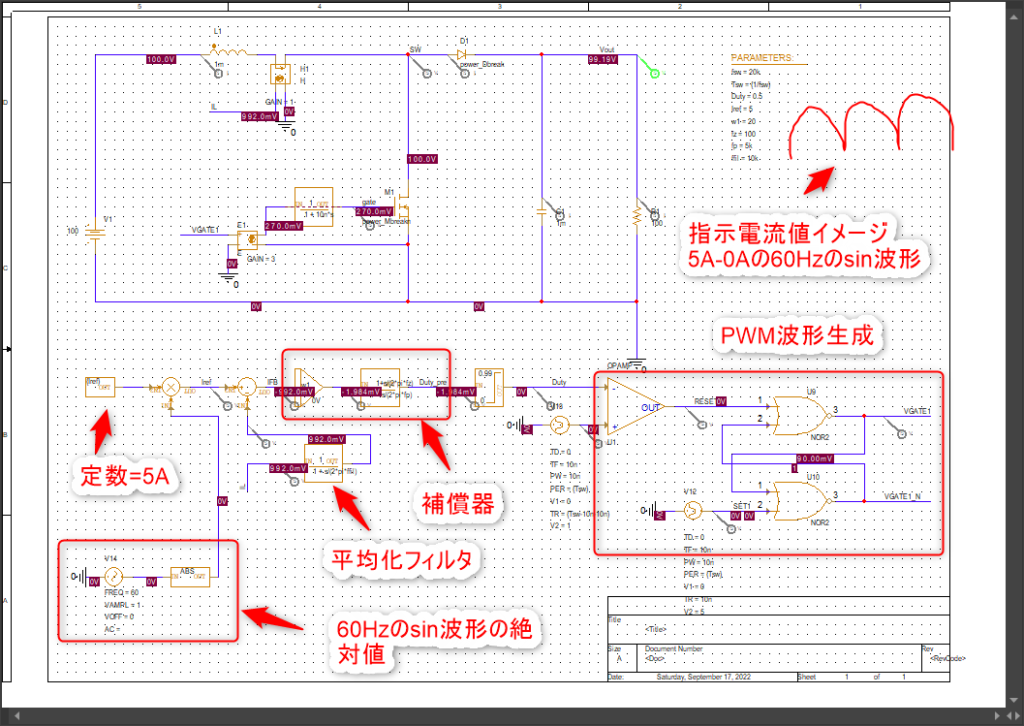
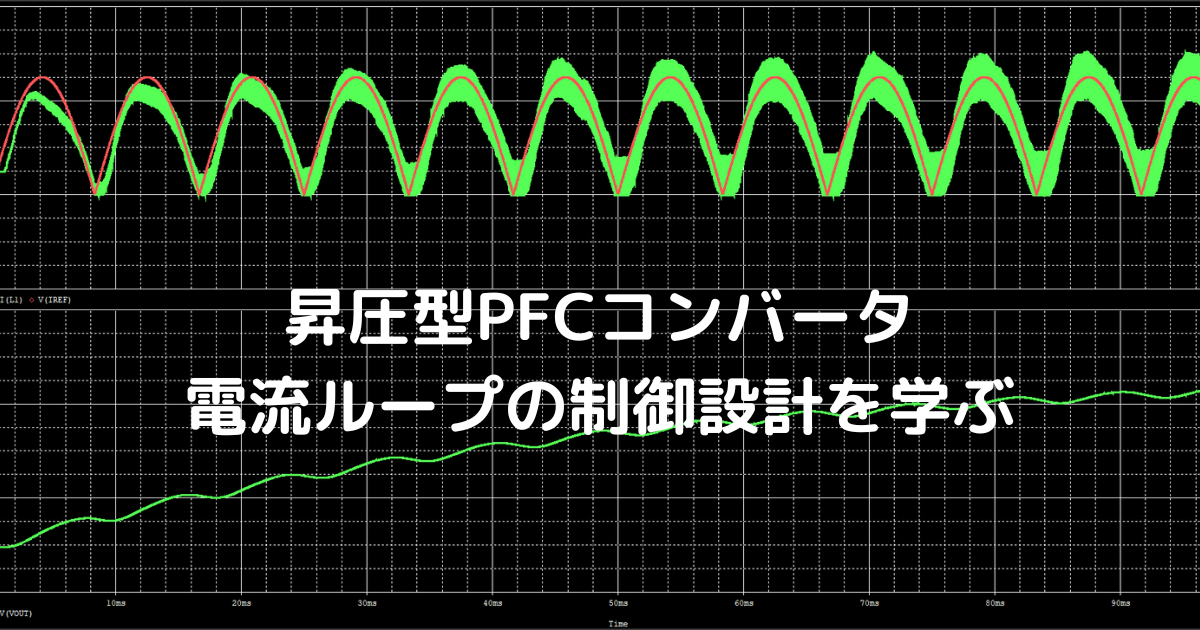
シミュレーション結果が以下になります。
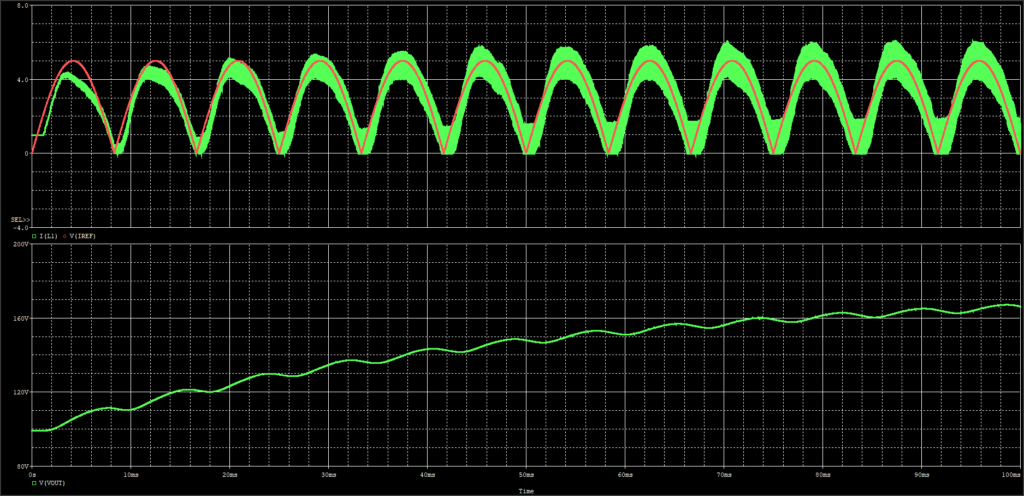
赤:指示電流Iref
緑:入力コイル電流
下段:出力電圧
電流の歪はあるものの、ちゃんと指示電流に追従していますね。オッケーでしょう。出力容量に電荷が貯まっていって、徐々に電圧が増加していって、リップル電流が大きくなっていってますね。
まぁ電流ループの設計は以上とします。
次は電圧ループの設計を勉強します。
以上です。誰かの参考になれば幸いです。最後までお読みいただきありがとうございました!!