前回記事で状態平均化法を使って非絶縁型降圧スイッチングレギュレータの伝達関数を導出しました。今回はその結果を用いて動作モデルをPspice for TIで作りましたので、その内容を報告します。
- 降圧スイッチングレギュレータの伝達関数
- 動作モデルの作り方
誰かの参考になれば幸いです。では、やってみます。
前回記事の結論
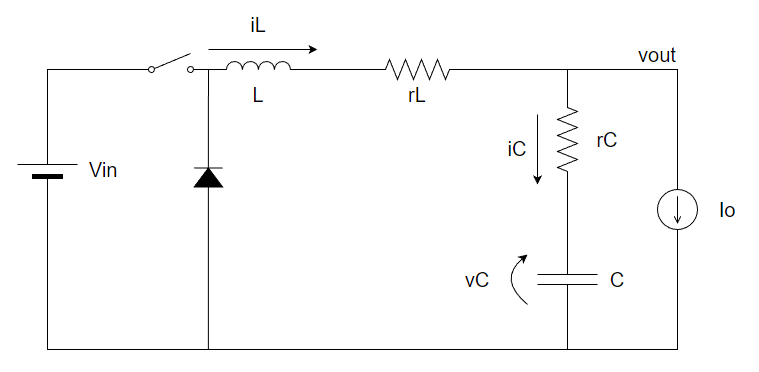
非絶縁型降圧スイッチングレギュレータの伝達関数は以下の通りになります。
$$\small{\frac{ΔVout(s)}{ΔVin}=G_{vv}=\frac{1}{P(s)} \left( 1+\frac{s}{ω_{esr}} \right) Duty}$$
$$\small{\frac{ΔVout(s)}{ΔDuty}=G_{dv}=\frac{1}{P(s)} \left( 1+\frac{s}{ω_{esr}} \right) Vin}$$
$$\small{\frac{ΔVout(s)}{ΔIo}=G_{iv}=-\frac{1}{P(s)} \left( s^2LCr_C+s(L+Cr_Lr_C)+r_L \right)}$$
ただし
$$\small{P(s)=\frac{s^2}{ω_n^2}+\frac{2δ}{ω_n}s+1}$$
$$\small{ω_n=\frac{1}{\sqrt{LC}},δ=\frac{r_L+r_C}{2}\sqrt{\frac{C}{L}},ωesr=\frac{1}{Cr_C}}$$
定常解(静特性)
$$\small{V_{out}=DutyVin-I_or_L}$$
Vin:入力電圧[V]、Vout:出力電圧[V]、Duty:スイッチングON DUTY[%]、L:出力コイルインダクタンス値[H]、C:出力コンデンサ容量値[F]、r_L:インダクタのDCR[Ω]、r_C:コンデンサのESR[Ω]、Io:出力電流[A]
導出過程の詳細は前回記事を参照してください。
Pspice for TIには伝達関数を表現する”LAPLACE”があるので、それを使って動作モデルを作ります。
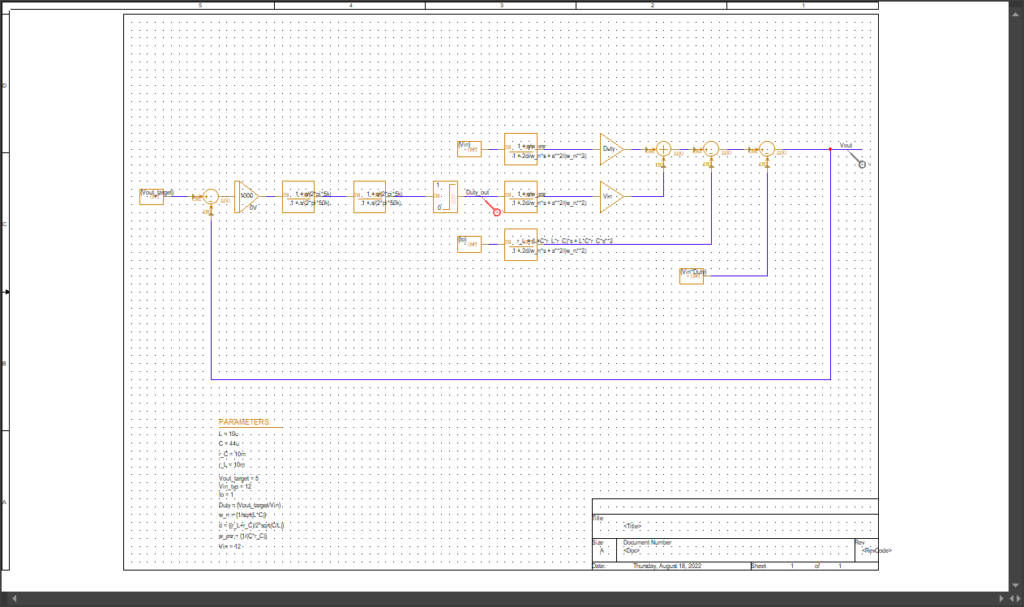
作成した動作モデル
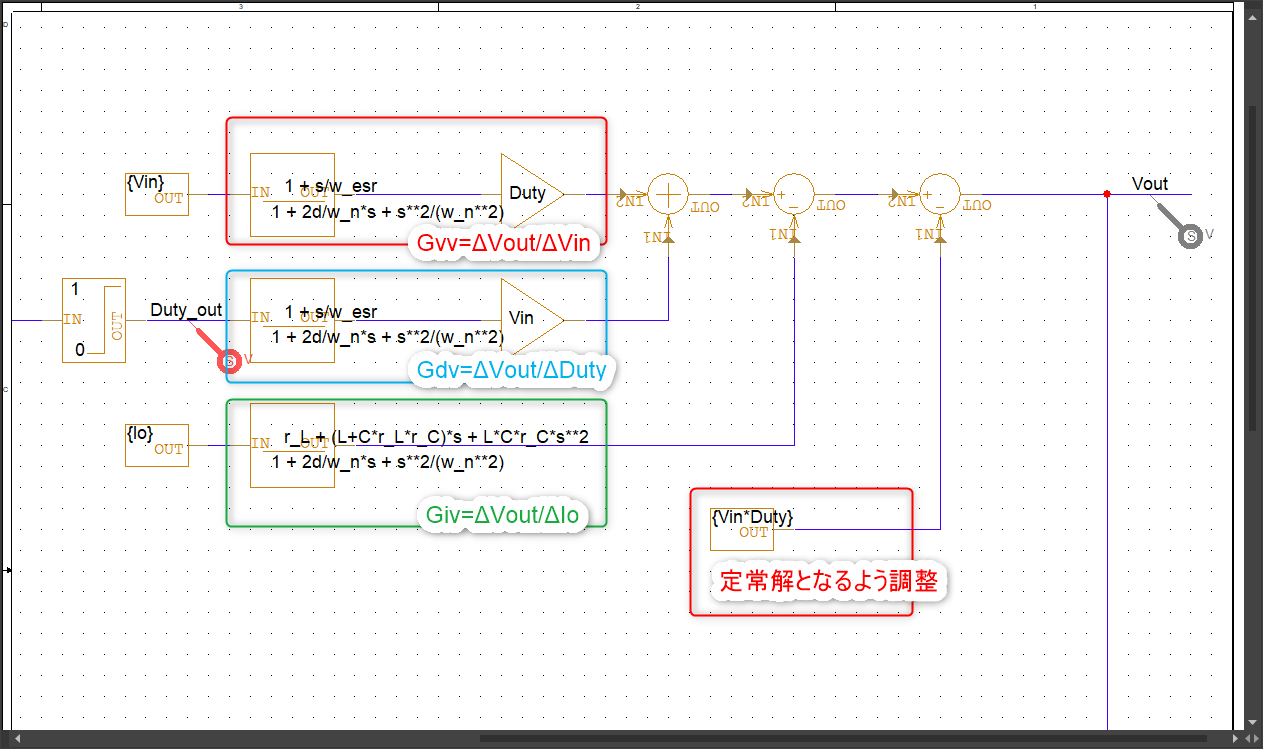
まず出力部分は以下のようにしました。最初に書いた伝達関数を全て足し合わせた形です。
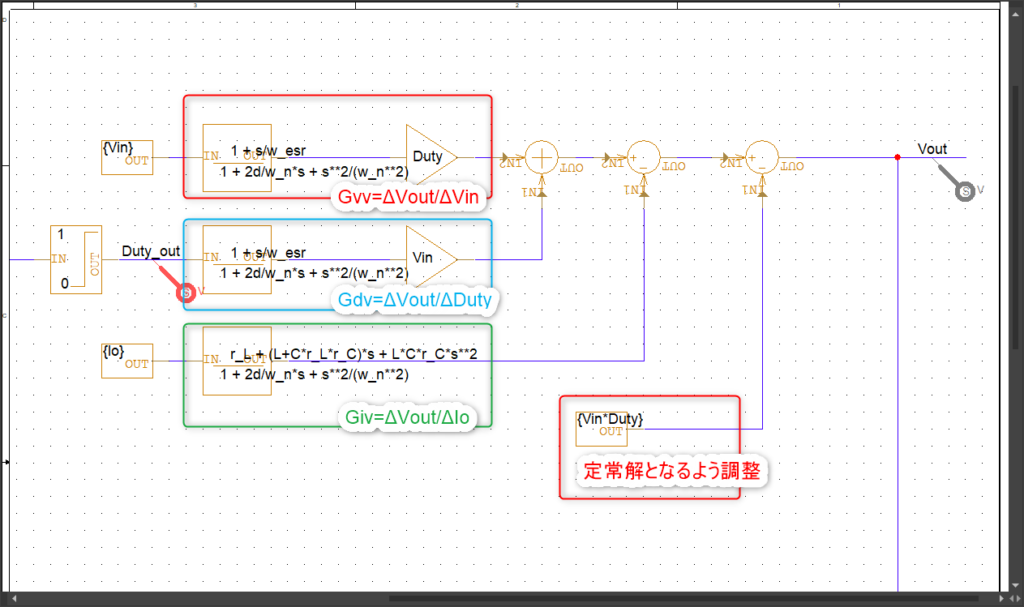
Vin,Duty,Ioの変動による出力の変動は以下の通り足し算になるからです。足すことで変動分を計算しています。(ΔIoに関しては符号が逆になるので注意です。)
$$\scriptsize{ΔVout(s)=\frac{1}{P(s)} \left( \left(1+\frac{s}{ω_{esr}} \right)DutyΔVin
+\left(1+\frac{s}{ω_{esr}} \right)VinΔDuty
-\left(s^2LCr_C+s(L+Cr_Lr_C)+r_L\right)ΔIo \right)}$$
それから定常解(静特性)を引き算しています。これはs=0を入れたときのそれぞれの出力を見たらわかるかと思うんですが、
$$\small{Gvv(s=0)=Vin*Duty, Gdv(s=0)=Vin*Duty, Giv(s=0)=r_L*Io\\
Vout(s=0)=Gvv+Gdv-Giv\\=Vin*Duty+Vin*Duty-r_L*Io\\=2Vin*Duty-r_L*Io}$$
とVoutが定常解Vin*Duty-r_L*Ioに比べてVin*Duty分だけ大きくなります。そのためVin*Duty分引き算して調整してあげてます。
次にフィードバック制御部です。
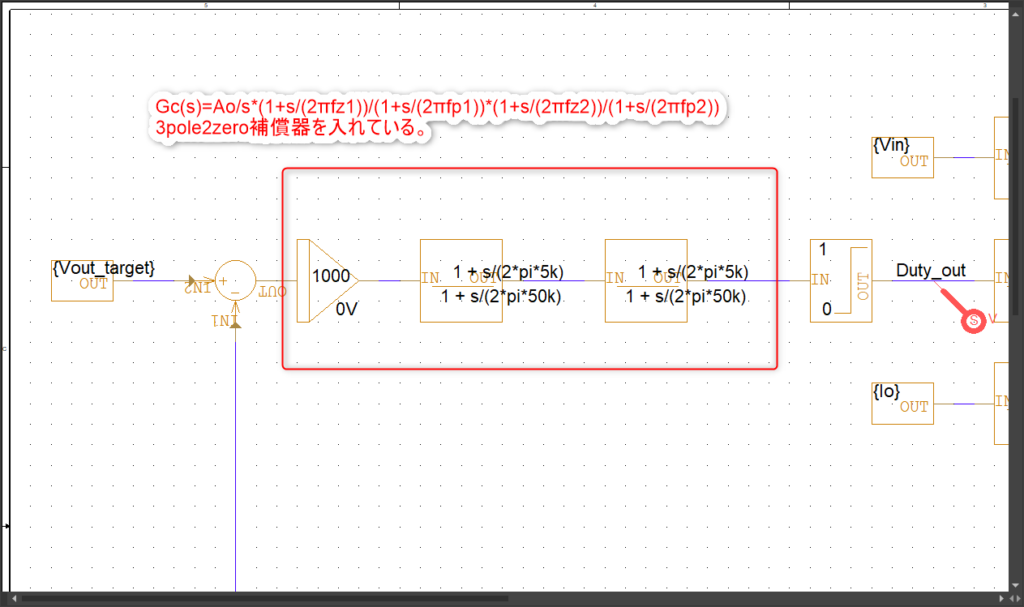
出力電圧の狙い値と比較して、Gc(s)のコントローラーでDutyを計算して、Limitで0~100%となるように制限を掛けてます。
Gc(s)は3pole2zero補償器を使用しています。(3個ポールがあって、2個ゼロがある。)電圧モード制御を行っているので、この補償器を使用しています。
$$\small{
G_c(s)=\frac{A_o}{s}\frac{1+\frac{s}{2pif_{z1}}}{1+\frac{s}{2pif_{p1}}}\frac{1+1+\frac{s}{2pif_{z2}}}{1+1+\frac{s}{2pif_{p2}}}
}$$
制御の係数はかなり適当に設定しています。
DCゲインAoはとりあえず60dBくらい。ゼロ点はLCの共振周波数が
$$\small{
f_{pLC}=\frac{1}{2pi\sqrt{LC}}\\
=\frac{1}{2pi\sqrt{10u*44u}}=7.587kHz
}$$
7.6kHzになるので、そのちょっと前の5kHzに2つゼロを入れとくかな。で設定しています。
ポールはなんとなく50kHz。適当です。
最後にパラメータ設定部です。

パラメータを設定しています。Vout=5V狙いで、Vin=12V、伝達関数のδ、ωn、ωesrもここで計算しています。まぁそれだけです。
ざっくりですが、これを非絶縁型降圧スイッチングレギュレータ(電圧モード制御)の動作モデルとしました。
シミュレーション結果
Vin電圧を6V~18Vまで変化しながら、t=10msの時間解析をしました。
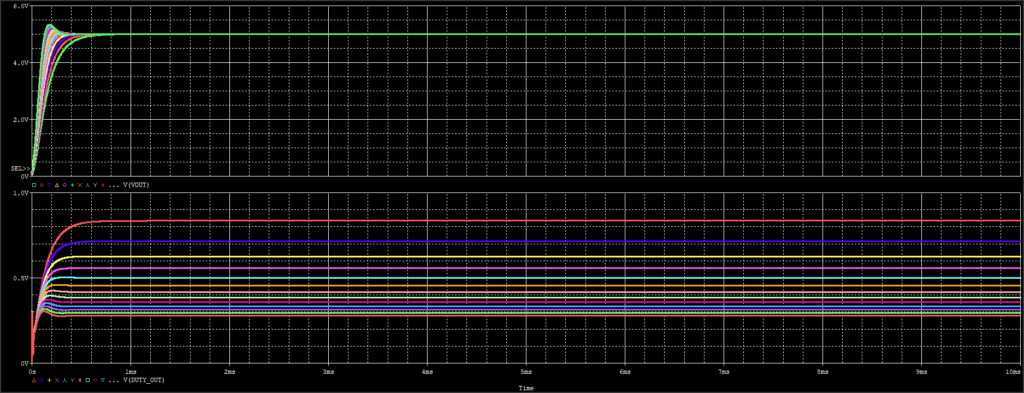
上:Vout
下:Duty
t=0ms~1msに拡大しました。
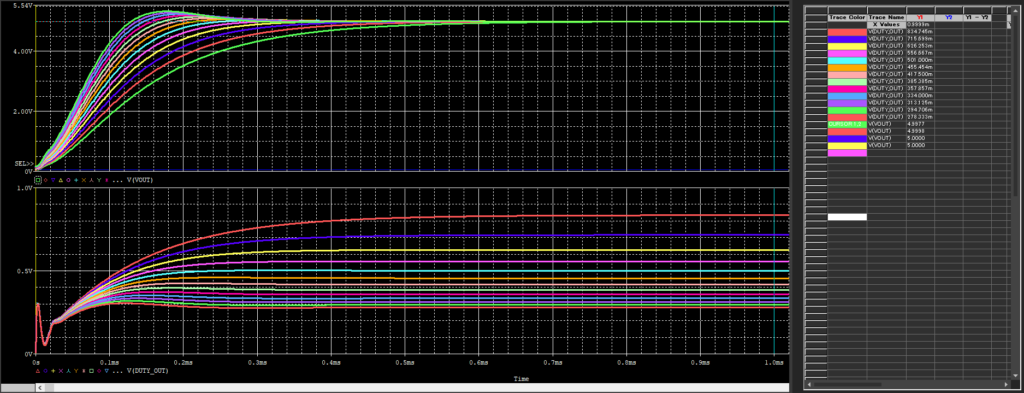
上:Vout
下:Duty
Voutは全て狙い値の5Vに収束していて問題なしですね。
Dutyはいくつも波形が出てきていてわかりずらいので、収束しているポイントでいくつになっているかを表にしました↓。
| Vin[V] | Duty(sim値)[%] | Duty(想定値=Vout/Vin)[%] |
|---|---|---|
| 6 | 83.47 | 83.00 |
| 7 | 71.57 | 71.43 |
| 8 | 62.63 | 62.50 |
| 9 | 55.67 | 55.56 |
| 10 | 50.10 | 50.00 |
| 11 | 45.55 | 45.45 |
| 12 | 41.75 | 41.67 |
| 13 | 38.54 | 38.46 |
| 14 | 35.79 | 35.71 |
| 15 | 33.40 | 33.33 |
| 16 | 31.31 | 31.25 |
| 17 | 29.47 | 29.41 |
| 18 | 27.83 | 27.78 |
想定値Vout/Vinと比較するとほとんど変わりないです。問題なしかと。
まとめとよくわからないこと
今回は非絶縁型降圧スイッチングレギュレータの動作モデルを作成しました。出力電圧をフィードバックしてDutyを制御する機能もモデル化しました(電圧モード制御)。
スイッチングしている様をシミュレーションでやってもらおうとするとかなり時間がかかってしまいます。ざっくりシステム全体の動作を見たいんよ。という用途には有用かと思います。
よくわからないこと
このモデルはVinとIoの瞬間的な変動に対してDutyが調整される様を見れない。
状態平均化せずにスイッチ=ONのときだけを行列で書いて、こんな感じ↓にしたらいいんだろうか?
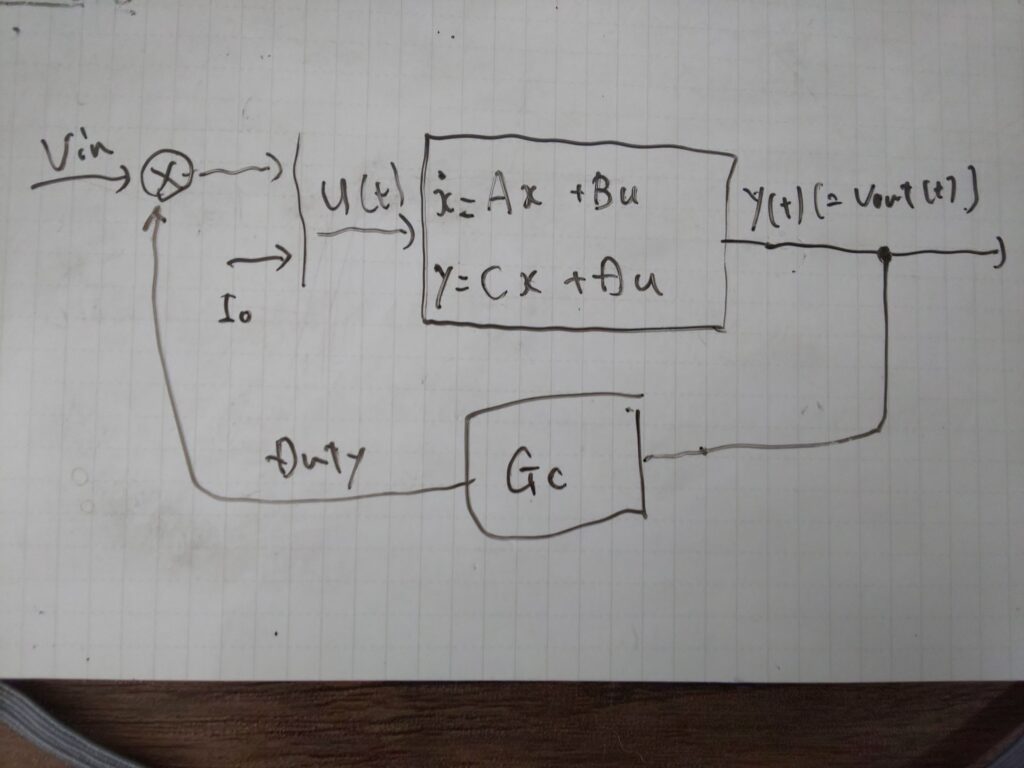
そういうシミュレーションしたいときはおとなしく回路書いてやったらいいんじゃないだろうか?
と思ったりしています。
はい、終わりです。誰かの参考になれば幸いです。最後までお読みいただきありがとうございました。