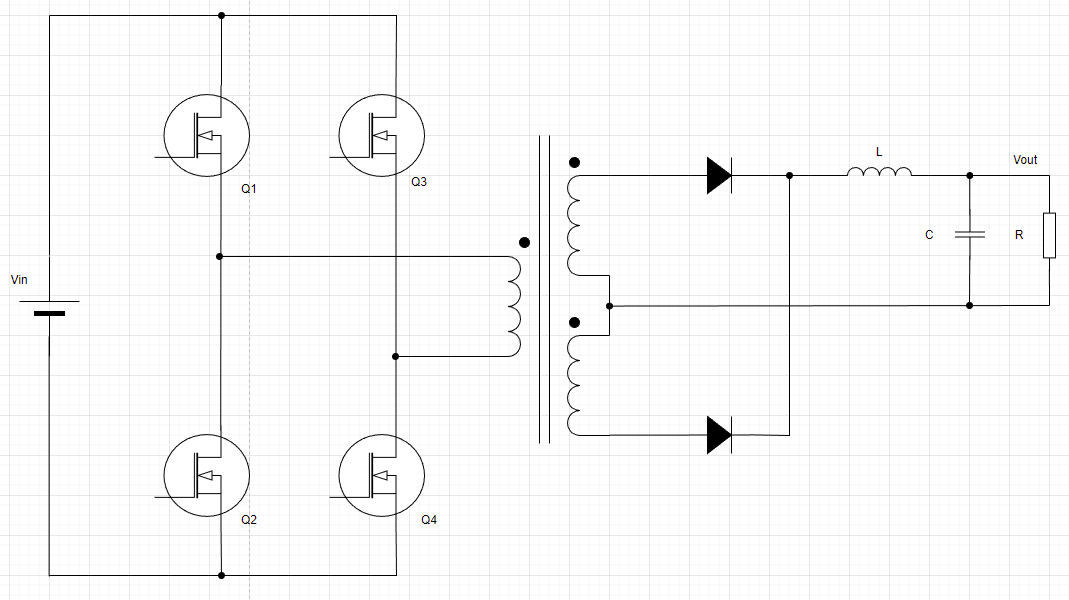
皆さん、お疲れ様です。フルブリッジコンバータご存知でしょうか。これです↓。
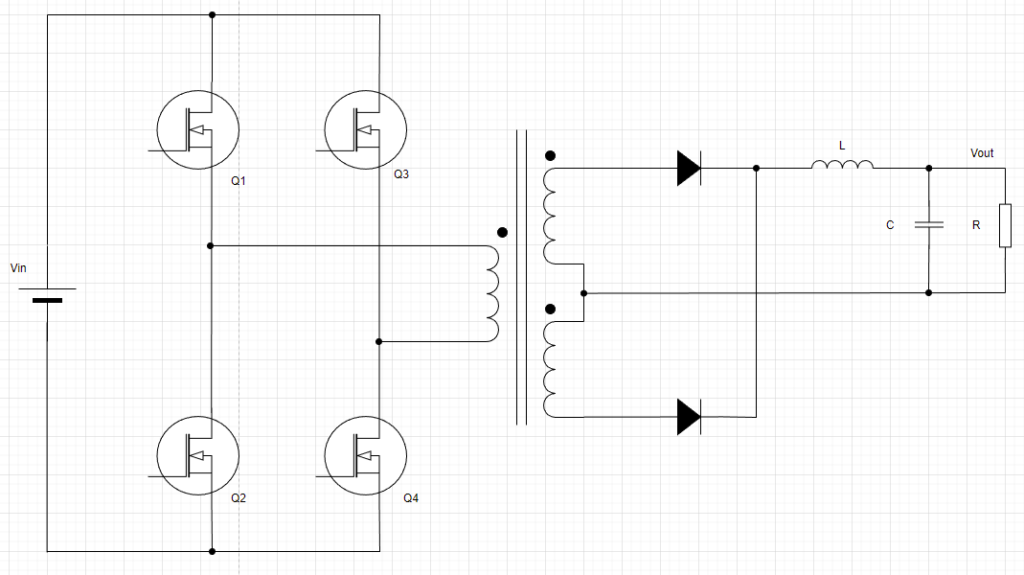
本日はフルブリッジコンバータの動作原理を解説してみようと思います。
・フルブリッジコンバータがどう動くのかわからん!!
・フルブリッジコンバータを見るのも嫌。
ということをお悩みの方の参考になれば幸いです。どういう動作をしてどういう理屈で出力電圧が決まるのか?を考えてきます。
ちなみにPSpice for TIにてフルブリッジコンバータの回路を作り、シミュレーションをしたって記事も書きました。気になる方は是非読んでみて下さい。
1回目:【電源回路】フルブリッジコンバータの動作原理(本記事)
2回目:【電源回路】フルブリッジコンバータの動作をシミュレーションで理解する
3回目:【電源回路】電圧モード制御フルブリッジコンバータの動作モデルを作った
4回目:【電源回路】フルブリッジコンバータの伝達関数
5回目:【電源回路】電流モード制御フルブリッジコンバータの動作モデルを作った
ではやっていきます。
結論と大事なこと
最初に結論です。出力電圧は以下の式で計算できます。
$$V_{out}=\frac{V_{in}}{n}D$$
コイル電流の交流成分は以下の式で計算できます。
$$Δi_{L}=\frac{\frac{V_{in}}{n}-V_{out}}{L}\frac{D}{2}T_{PWM}$$
Vout:出力電圧[V]
Vin:入力電圧[V]
n:変圧器の巻き線比
ΔiL:コイル電流の増減分[A]
L:出力コイルのインダクタンス値[H]
D:スイッチ(Q1~Q4)のON DUTY[%]
まぁこれは式を解いていけばわかります。これを導くのに大事な大事な考え方があります。それは、、、
一周期のスイッチON/OFF時のコイル電流の増減は足し合わせると0になる!!!
です。
なぜその考え方で導けるかというと、
一周期のコイル電流が増減したら、出力電圧が変わっちゃうから!増分がコンデンサに貯められる=出力電圧が上がってるってことだから!
コイル電流の増減を足し合わせると0になってないと出力電圧が一定でなくなってしまうからです。
まず1周期Tpmwの動作を解説
フルブリッジコンバータでは1周期間で4つの動作をします。
- Q1,Q4がON
- 全部OFF
- Q2,Q3がON
- 全部OFF
この1~4をやって1周期です。一個ずつ解説しますかね。
Q1,Q4がON
まずはQ1とQ4がONとなります。こうですね↓。
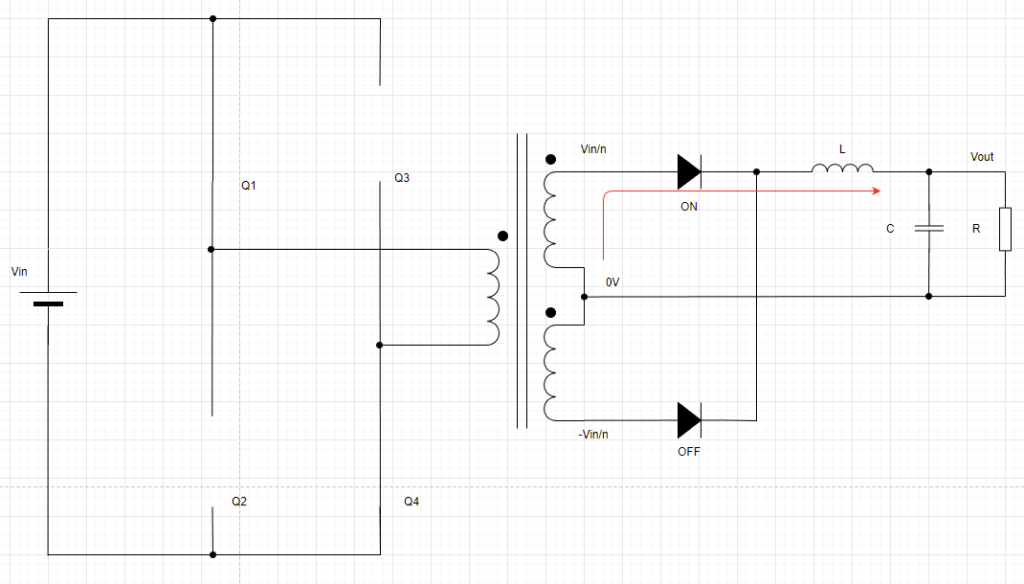
1次側のトランスにVinの電圧がかかるため、2次側には巻き線比nに応じてVin/nの電圧がかかります。
コンデンサCと抵抗Rの下側を基準(=0V)なので、上側のダイオードのみがONします。
このときコイルLにはVin/n-Voutの電圧がかかることになります。
コイルLの電流を計算してみましょう。
コイルの式を思い出しましょう。
$$V_L=L\frac{Δi_L}{Δt}$$
$$Δi_L=\frac{V_L}{L}Δt$$
この式に出力コイルにかかっている電圧や時間を入れていきます。
$$Δi_{L1}=\frac{\frac{V_{in}}{n}-V_{out}}{L}D_1T_{PWM}$$
D1:Q1,Q4のON DUTY[%]
Tpwm:1周期[sec]
はい、このΔiL1を書いたら次です。
全部OFF①
次にQ1,Q4がOFFします。こうですね↓。
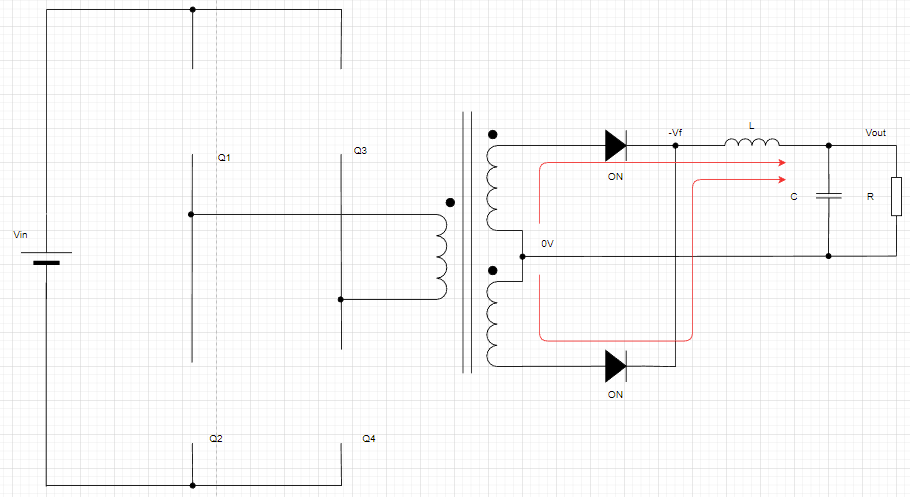
1次側のトランスには電圧がかかりません。2次側ではLの逆起電力により、2つのトランスから電流を引っ張ります。
コイルLには-Vf-Voutの電圧がかかることになります。(-Vfは簡単のために≒0Vとします。)
同じくコイル電流を計算します。
$$Δi_{L2}=\frac{-V_{out}}{L}D_1’T_{PWM}$$
D1’:Q1,Q4のOFF DUTY[%](1-D1のこと)
はい、このΔiL2を書いたら次です。
Q2,Q3がON
次にQ2,Q3がONします。このDUTY比はQ1,Q4と同じです。
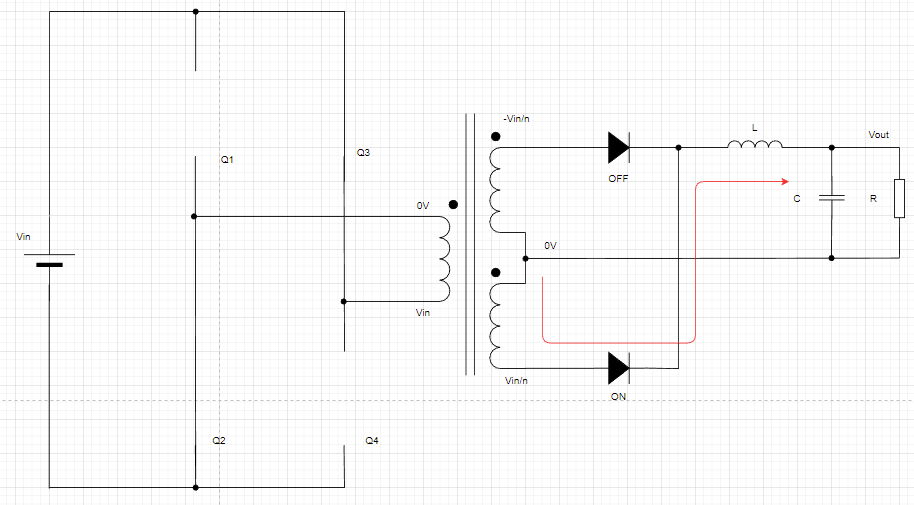
1次側コイルには巻き線方向とは逆にVin電圧がかかることになります。
2次側コイルは巻き線比に応じてVin/n電圧がかかることになります。
下側のみのダイオードがONして動きます。
このときコイルLにはQ1,Q4がONしたときと同じようにVin/nの電圧がかかります。
コイル電流を計算します。
$$Δi_{L3}=\frac{\frac{V_{in}}{n}-V_{out}}{L}D_2T_{PWM}$$
D2:Q2,Q3のON DUTY[%]
はい、このΔiL3を書いたら次です。
全部OFF②
最後にQ2,Q3がOFFします。このときの動きは前回OFFとなったときと同じになります。ちなみにOFF DUTY比はQ1,Q4のOFF DUTY比と同じです。

同じくコイル電流を計算します。
$$Δi_{L4}=\frac{-V_{out}}{L}D_2’T_{PWM}$$
D2’:Q2,Q3のOFF DUTY[%](1-D2のこと)
はい、これで準備完了です。
出力電圧の導出過程
じゃあ、出力電圧値はどう決まるのか?を計算してみようと思います。そのときに大事な考え方は最初に言いましたが、
一周期のスイッチON/OFF時のコイル電流の増減は足し合わせると0になる!!!
です。この考え方をそのまま式を表すと以下のようになります。
$$Δi_{L1}+Δi_{L2}+Δi_{L3}+Δi_{L4}=0$$
簡単ですね。これを解いて行くと出力電圧の式が出てきます。とりあえず代入します。
$$\frac{\frac{V_{in}}{n}-V_{out}}{L}D_1T_{PWM}+\frac{-V_{out}}{L}D_1’T_{PWM}+\frac{\frac{V_{in}}{n}-V_{out}}{L}D_2T_{PWM}+\frac{-V_{out}}{L}D_2’T_{PWM}=0$$
LとTpwmを消します。
$$(\frac{V_{in}}{n}-V_{out})D_1-V_{out}D_1’+(\frac{V_{in}}{n}-V_{out})D_2-V_{out}D_2’=0$$
まとめます。
$$(\frac{V_{in}}{n}-V_{out})(D_1+D_2)-V_{out}(D_1’+D_2′)=0$$
だいぶすっきりしました。ここでD1=D2なので、Q1~Q4のON DUTYの合計をD、OFF DUTYの合計をD’とすると、、、
$$D_1=D_2$$
$$D_1+D_2=2D_1=D$$
$$D_1’+D_2’=2D_1’=D’$$
となります。すると以下のようになります。
$$(\frac{V_{in}}{n}-V_{out})2D_1-V_{out}2D_1’=0$$
$$(\frac{V_{in}}{n}-V_{out})D-V_{out}D’=0$$
$$(\frac{V_{in}}{n}-V_{out})D-V_{out}(1-D)=0$$
展開して計算します。
$$\frac{V_{in}}{n}D-V_{out}D-V_{out}+V_{out}D=0$$
$$\frac{V_{in}}{n}D-V_{out}=0$$
$$V_{out}=\frac{V_{in}}{n}D$$
はいこれで終わりです。なんだ結局、非絶縁タイプの降圧DCDCに巻き線比nが加わっただけじゃんってなりましたね。
コイル電流は既に計算済みですが、Dを使って表すと以下のようになります。
$$Δi_{L}=\frac{\frac{V_{in}}{n}-V_{out}}{L}\frac{D}{2}T_{PWM}$$
はい以上になります。誰かの参考になれば幸いです。最後までお読みいただきありがとうございました!!!