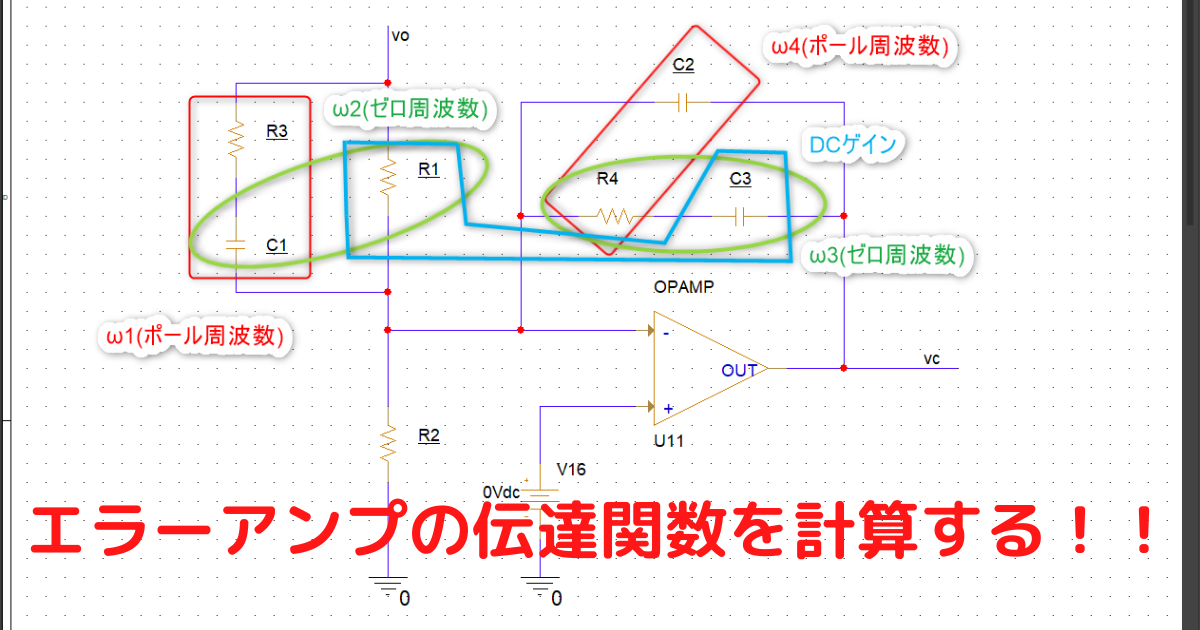
今日はDCDCをやってる人は見たことがあるであろう、以下のType3補償器と言われる電圧アンプの伝達関数を導出してみよう。という記事です。
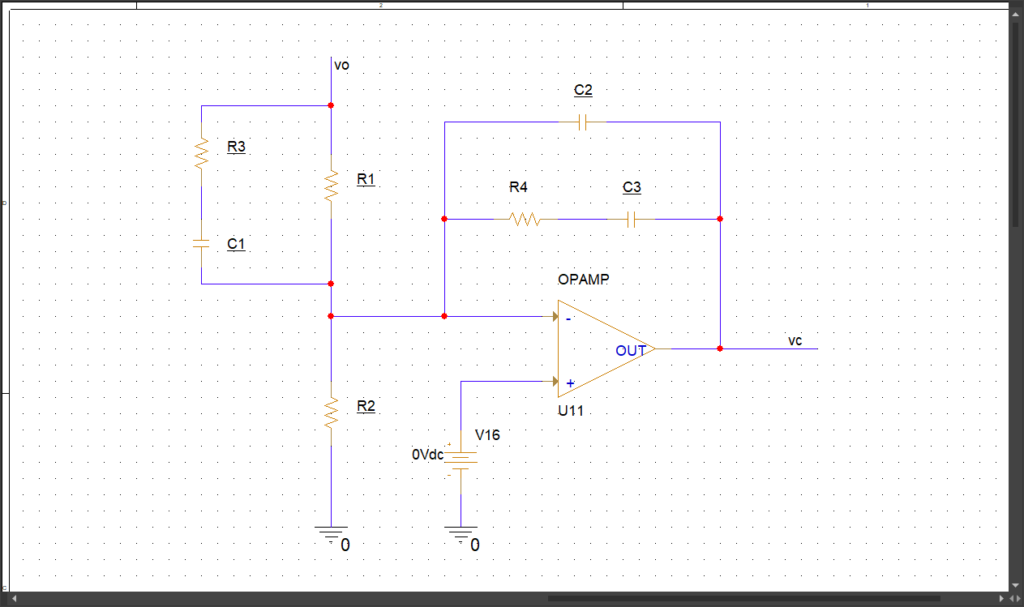
Type3補償器の伝達関数わかんねー。という方は読んで頂ければと思います。
結論:伝達関数vc/voはこれ
$$\normalsize{
\frac{v_c}{v_o}=-\frac{1}{R_1C_3}\frac{1}{s}
\frac{1+\frac{s}{ω_{2}}}{1+\frac{s}{ω_{1}}}
\frac{1+\frac{s}{ω_{3}}}{1+\frac{s}{ω_{4}}}
}$$
$$\small{ω_{1}=\frac{1}{C_1R_3},ω_{2}=\frac{1}{C_1R_1},ω_{3}=\frac{1}{C_3R_4},ω_{4}=\frac{1}{C_2R_4}}$$
回路図のどこ?っていうのを書くとこうですね↓。
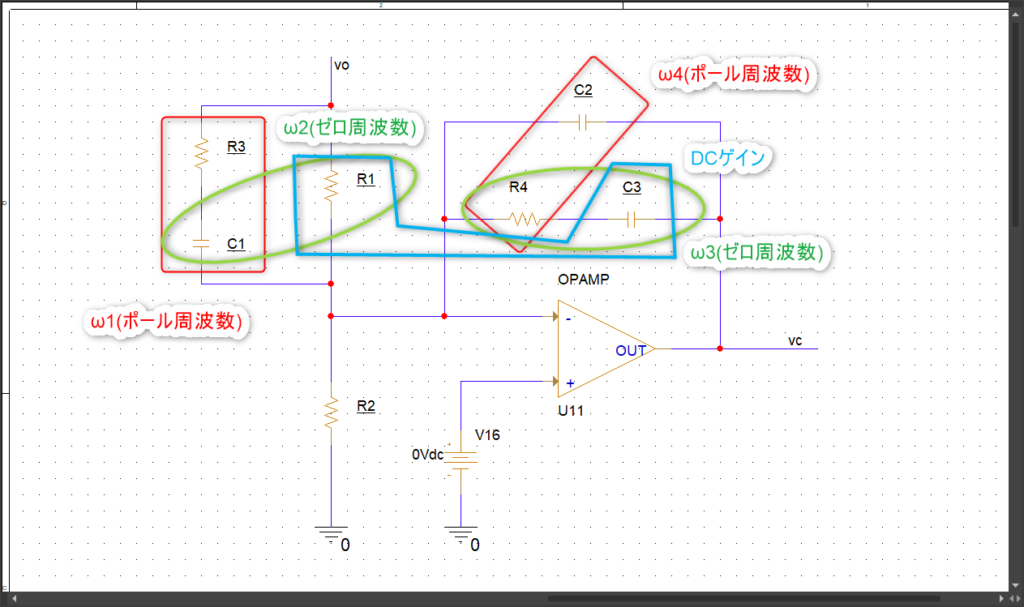
準備:RCをまとめる
ごちゃごちゃした部分をまとめます。
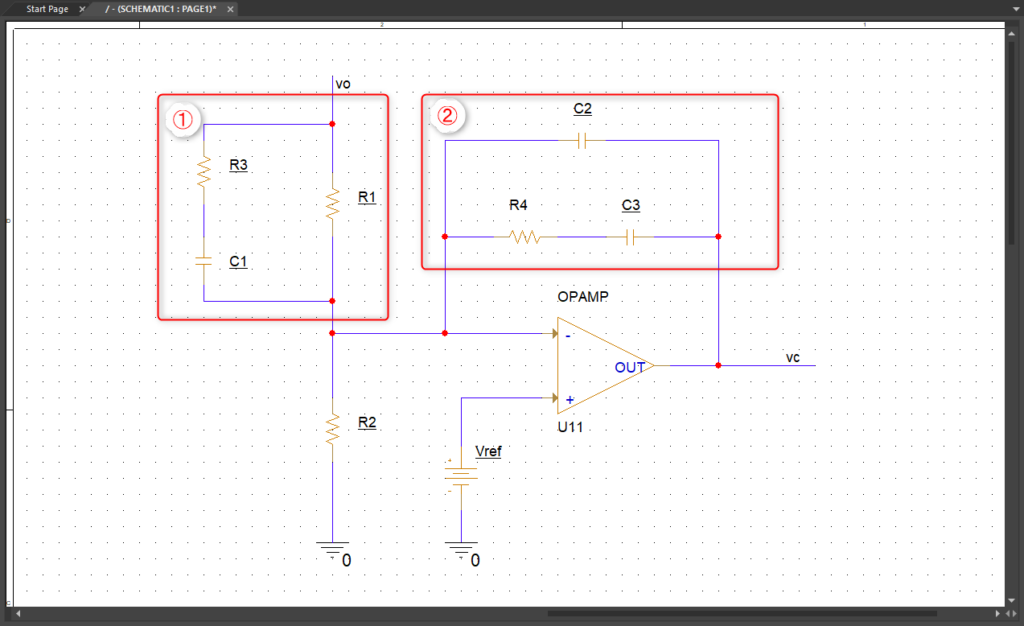
①と②をまとめてしまいましょう。まず①から。
コンデンサを1/sCと置き換えて、R3と直列で繋がり、それがR1と並列で繋がっているので、合成抵抗Z1は以下のように計算できます。
$$\small{
Z_1=(R_3+\frac{1}{sC_1})//R_1\\
Z_1=\frac{R_1(R_3+\frac{1}{sC_1})}{R_1+R_3+\frac{1}{sC_1}}\\
Z_1=R_1\frac{R_3+\frac{1}{sC_1}}{R_1+R_3+\frac{1}{sC_1}}\\
}$$
分子分母にsC1を掛けます。
$$\small{
Z_1=R_1\frac{sC_1R_3+1}{sC_1(R_1+R_3)+1}
}$$
綺麗な形にすると以下のようになります。
$$\small{Z_1=R_1\frac{1+\frac{s}{ω_{1}}}{1+\frac{s}{ω_{2}}}}$$
ただし
$$\small{ω_{1}=\frac{1}{C_1R_3},ω_{2}=\frac{1}{C_1(R_1+R_3)}}$$
続いて②です。同様にコンデンサを1/sCとして合成抵抗Z2を計算すると以下のようになります。
$$\small{
Z_2=(R_4+\frac{1}{sC_3})//\frac{1}{sC_2}\\
Z_2=\frac{(R_4+\frac{1}{sC_3})\frac{1}{sC_2}}{R_4+\frac{1}{sC_3}+\frac{1}{sC_2}}\\
}$$
sC2C3を分子分母に掛けたくなるのが人情ですね。
$$\small{
Z_2=\frac{(R_4+\frac{1}{sC_3})C_3}{sC_2C_3R_4+C_2+C_3}\\
Z_2=\frac{C_3R_4+\frac{1}{s}}{sC_2C_3R_4+C_2+C_3}
}$$
sを掛けます。
$$\small{
Z_2=\frac{1}{s}\frac{sC_3R_4+1}{sC_2C_3R_4+C_2+C_3}\\
Z_2=\frac{1}{s}\frac{1}{C_2+C_3}\frac{sC_3R_4+1}{s\frac{C_2C_3R_4}{C_2+C_3}+1}
}$$
綺麗に書くと
$$\small{
Z_2=\frac{1}{s}\frac{1}{C_2+C_3}\frac{\frac{s}{ω_{3}}+1}{\frac{s}{ω_{4}}+1}
}$$
ただし
$$\small{ω_{3}=\frac{1}{C_3R_4},ω_{4}=\frac{C_2+C_3}{C_2C_3R_4}}$$
これで多少すっきりしました↓。
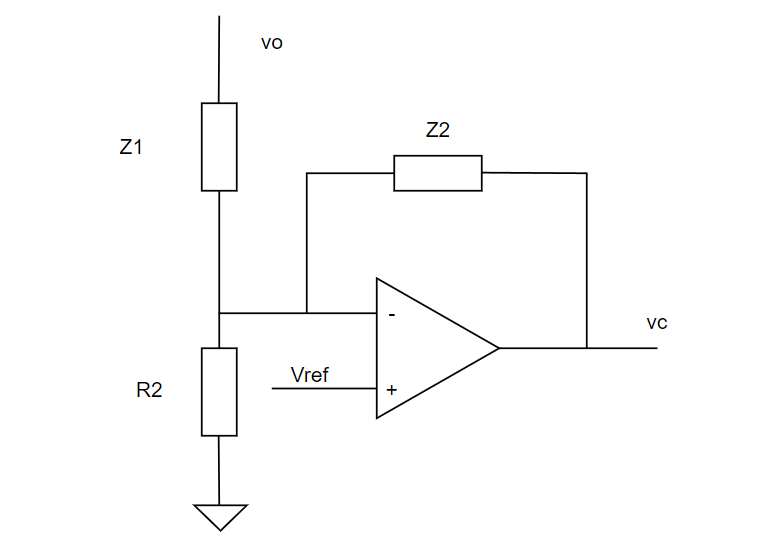
はい、準備はここまでです。次です。
オペアンプのゲインを∞として式を立てる
オペアンプのゲインはとても大きいので∞とすると、とても簡単に計算できます。
イマジナリーショート(仮想接地)となり、小信号で考えるとオペアンプの入力は0Vとなります。
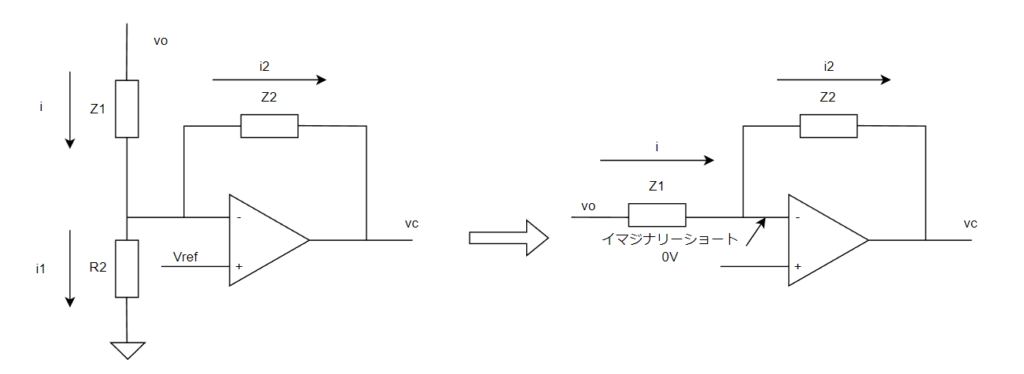
小信号ではi=i2なのでそれを式にします。
$$\small{
i=i_2\\
\frac{v_o}{Z_1}=\frac{0-v_c}{Z_2}
}$$
これをvc/vo=となるように解きます。
$$\small{
\frac{v_o}{v_c}=-\frac{Z_1}{Z_2}\\
\frac{v_c}{v_o}=-\frac{Z_2}{Z_1}
}$$
あとはZ1とZ2を元に戻したら終わりです。
$$\small{
Z_1=R_1\frac{1+\frac{s}{ω_{1}}}{1+\frac{s}{ω_{2}}}\\
Z_2=\frac{1}{s}\frac{1}{C_2+C_3}\frac{\frac{s}{ω_{3}}+1}{\frac{s}{ω_{4}}+1}
}$$
代入します。
$$\normalsize{
\frac{v_c}{v_o}=-\frac{\frac{1}{s}\frac{1}{C_2+C_3}\frac{\frac{s}{ω_{3}}+1}{\frac{s}{ω_{4}}+1}}{R_1\frac{1+\frac{s}{ω_{1}}}{1+\frac{s}{ω_{2}}}}
}$$
綺麗にします。
$$\normalsize{
\frac{v_c}{v_o}=-\frac{1}{R_1(C_2+C_3)}\frac{1}{s}
\frac{1+\frac{s}{ω_{2}}}{1+\frac{s}{ω_{1}}}
\frac{1+\frac{s}{ω_{3}}}{1+\frac{s}{ω_{4}}}
}$$
$$\small{ω_{1}=\frac{1}{C_1R_3},ω_{2}=\frac{1}{C_1(R_1+R_3)},ω_{3}=\frac{1}{C_3R_4},ω_{4}=\frac{C_2+C_3}{C_2C_3R_4}}$$
一般的にC3>>C2かつR1>>R3で設定するので、C2+C3≒C3、R1+R3≒R1とします。
$$\normalsize{
\frac{v_c}{v_o}=-\frac{1}{R_1C_3}\frac{1}{s}
\frac{1+\frac{s}{ω_{2}}}{1+\frac{s}{ω_{1}}}
\frac{1+\frac{s}{ω_{3}}}{1+\frac{s}{ω_{4}}}
}$$
$$\small{ω_{1}=\frac{1}{C_1R_3},ω_{2}=\frac{1}{C_1R_1},ω_{3}=\frac{1}{C_3R_4},ω_{4}=\frac{1}{C_2R_4}}$$
出てきましたね。これがType3補償器の伝達関数です。
ポール:ω1,ω4
ゼロ:ω2,ω3
DCゲイン:1/(R1C3)

はい、以上です。イマジナリーショートを使うと意外と簡単に計算できます。
最後までお読みいただきありがとうございました!!