みなさま、お疲れ様です。
本記事はチョークコイルやトランスの磁束密度を計算する以下の式について考えてみようと思います。
$$\small{
ΔB=\frac{V・t}{2N・A_e}…(交流電圧印加の場合)\\
ΔB=\frac{V・t}{N・A_e}…(直流電圧印加の場合)
}$$
ΔB:磁束密度[Wb/m2]、V:印可電圧[V]、t:印加時間[s]、N:巻き線数、Ae:コア断面積
ちなみにこの式は以下の参考書のP36に記載されています。
磁束密度はなんでこの式で計算できるのかわからない!
とお悩みの方の参考になれば幸いです。では、始めます。
基本知識
ファラデーの電磁誘導の法則
まず、ファラデーの電磁誘導の法則は以下の式になります。
$$\small{
V=N\frac{ΔΦ}{Δt}
}$$
この式は「巻き線数NのコイルにΔt時間でΔΦの磁束が変化したら、起電圧Vが発生します。」
という意味です。高校生のときの式ですね。懐かしいですか?私は忘れてました。
磁束密度の意味
以下のようにコイルに電圧をかけるとファラデーの法則で磁束がコア断面積Aeに流れます。
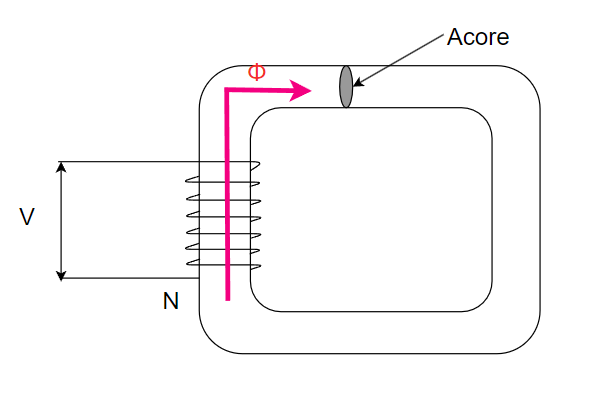
磁束密度は一定の面積あたりどんだけの磁束が流れているか?ということです。
つまり式にすると
$$\small{
B=\frac{Φ}{A_e}
}$$
です。
つまり、たとえば、
太っとい磁性体であれば、磁束密度Bは小さくなります。
逆に細っそい磁性体であれば、磁束密度Bは大きくなります。
電気工学の世界で細っそい銅線に電流を流すのと太っとい銅線に電流を流すのでは、電流密度が違います。電磁気の世界で電流密度に当たるものが磁束密度です。
細っそい銅線に許容電流量を超えて流すと燃えるのと同じように細っそい磁性体コアに最大磁束密度を超えて磁束を流すと磁気飽和を起こします。
最初の式を導出してみる
ファラデーの法則の式をΔΦ=の形にします。
$$\small{
ΔΦ=\frac{V・Δt}{N}
}$$
そして、磁束密度の式もΦ=の形にします。
$$\small{
Φ=B・A_e
}$$
この式を上の式に代入します。
$$\small{
ΔB・A_e=\frac{V・Δt}{N}
}$$
ΔB=の形にします。
$$\small{
ΔB=\frac{V・Δt}{N・A_e}
}$$
はい、これで磁束密度の式が出てきました。
では、なぜ交流電圧を印可すると1/2となるのでしょうか。
なぜ交流電圧印可だと1/2がつくのか?
簡単です。そりゃ、だって交流だから±の電圧が印可されるからです。
+電圧が印可されているときは+ΔBの磁束密度の変化が生じて、
-電圧が印可されているときは-ΔBの磁束密度の変化が生じています。
つまり総量としては2ΔBの磁束が変化しています。つまりつまり、交流の場合、式は以下になります。
$$\small{
2ΔB=\frac{V・Δt}{N・A_e}
}$$
2を払うと
$$\small{
ΔB=\frac{V・Δt}{2N・A_e}
}$$
こうなると。
はい、以上で本記事を終わりです。
誰かの参考になれば幸いです。最後までお読みいただきありがとうございました!!!