【インバーター】プラントGdiの周波数特性をLTspiceで確認する

みなさま、お疲れ様です。単相インバーターを勉強する記事、4回目です。

第2回目で電流プラントGdi(s)の伝達関数を以下の式だと導出しました。

$$\small{
G_{di}(s)=\frac{ΔIL(s)}{ΔD(s)}=\frac{2V_{dc}}{sL}\\
}$$

これが正しいの？を確認しよう。というのが本記事の目的です。

という方(そんな人いるのかな？)の悩みの一助となれば幸いです。

電流プラントGdi(s)の周波数特性のボード線図を描く

まず導出した式↓のボード線図を描いてみます。

$$\small{
G_{di}(s)=\frac{ΔIL(s)}{ΔD(s)}=\frac{2V_{dc}}{sL}\\
}$$

今回はVdc=200V、L=1mHと想定します。

これをpythonのcontrolライブラリを使って描きました。以下のようになりました↓。

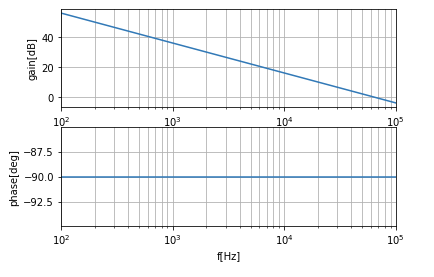
分母にsがいる形なので、一直線にゲインが20dB/decで落ちていってます。

ちなみにボード線図を描くスクリプトは以下の通りです。

#import
import math
import numpy as np
from matplotlib import pyplot as plt
import sympy as sym
import control as ctl

L=1e-3#インダクタンス値
C=5e-6#出力コンデンサ容量値
Vdc=200#DC電圧

Gdi = ctl.tf([2*Vdc],[L,0])#電流制御のプラント伝達関数

#プラントのボード線図の計算
f_list = 10**np.linspace(2, 5, 51)#周波数範囲
w_list = 2 * np.pi * f_list#角周波数に変換
gain_plant, phase_plant, w = ctl.bode(Gdi, w_list ,Plot=False)
f = w/2/np.pi#単位を[rad/sec]を[Hz]に変換
gain_plant_dB = 20*np.log10(gain_plant)#単位を[dB]に変換
phase_plant_deg = phase_plant * 180/np.pi#単位を[rad]から[deg]に変換

#ボード線図表示
fig, ax = plt.subplots(2,1)
ax[0].semilogx(f, gain_plant_dB)

ax[0].set_xlim(100, 10**5)
ax[0].grid(which = "both", axis = "x")
ax[0].grid(which = "both", axis = "y")
ax[0].set_ylabel("gain[dB]")
ax[1].semilogx(f, phase_plant_deg)
ax[1].set_xlim(100, 10**5)
ax[1].grid(which = "both", axis = "x")
ax[1].grid(which = "both", axis = "y")
ax[1].set_ylabel("phase[deg]")
ax[1].set_xlabel("f[Hz]")

これが実際に回路で測定するとどうなるかを見てみます。

電流プラントGdi(s)の周波数特性をLTspiceで測定する

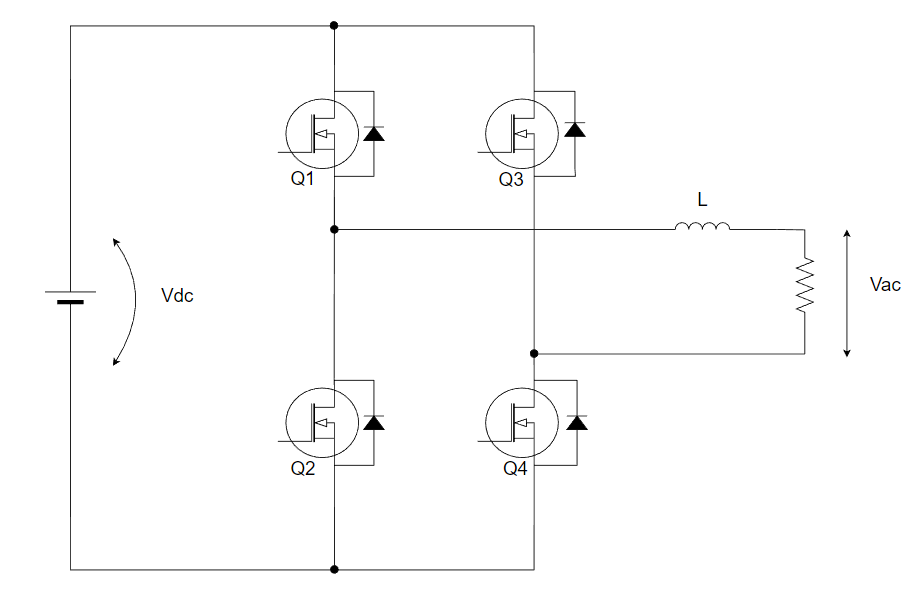
確認用回路図は以下の通りです↓。

回路図自体はほぼ第3回目で使用した回路図と同じです。

どうやって周波数特性を測定しているのか？については過去記事で解説しておりますので、そちらを参照頂ければ幸いです。

7msecのシミュレーションを51回実行しておりますので、シミュレーション時間がめちゃ長いです。今回は2時間くらいかかりました。

それで得られた特性が以下の通りです↓。

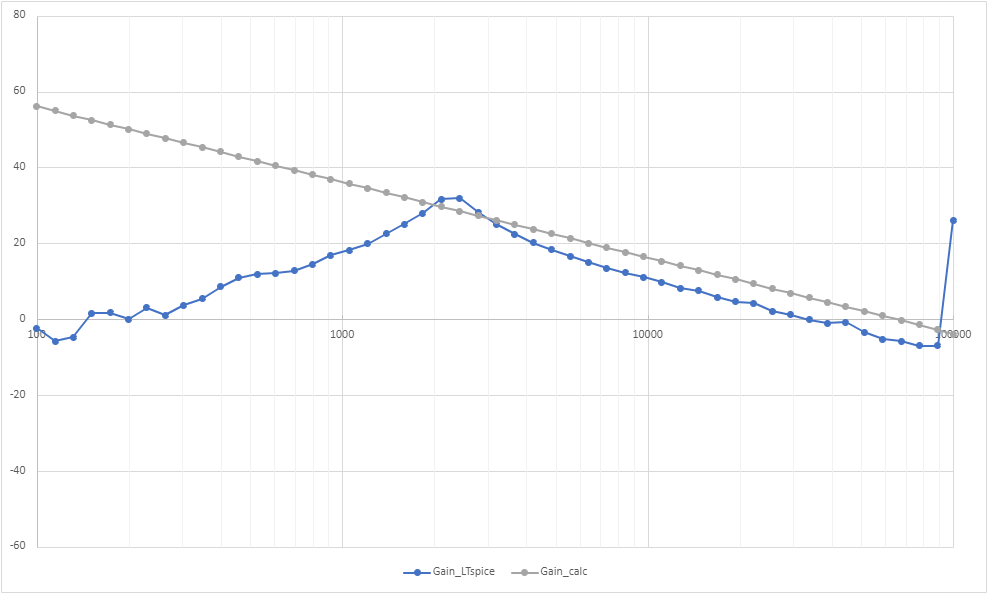
先ほど示した理論式が灰色でプロットしており、LTspiceで得られた結果を青色でプロットしています。

3kHzより早い周波数ではほぼ想定通りです。

3kHzより遅い周波数では違いますね。この差は何で？ってなりますが、わかりません(笑)

細かく小信号解析したらそうなるんでしょうね(適当)。

過去にPFCコンバータを勉強したときに「伝達関数が以下↓になるよ。」って論文を見ましたが、

$$\small{
G_{di-R}(s)=\frac{2V_{rms}}{RD’^3}\frac{1+\frac{sCR}{2}}{Δ(s)}\\
Δ(s)=\frac{s^2}{ω_o^2}+\frac{s}{ω_oQ_o}+1\\
ω_o=\frac{D’}{\sqrt{LC}},Q_o=\frac{R}{Lω_o}
}$$

「で、結局近似式は以下↓だよ。」ってなってました。それと同じでしょう。たぶん。

$$\small{
G_{di-app}(s)=\frac{Vo}{sL}
}$$

ちなみにその論文はこれです。

なので、まぁ結論としては、、、

クロスオーバー周波数はスイッチング周波数100kHzの1/10程度と考えると、近似式として2Vdc/sLは問題なく使えるかなと考えてます。

はい、そんな感じで終わります。

誰かの参考になれば幸いです。最後までお読みいただきありがとうございました。