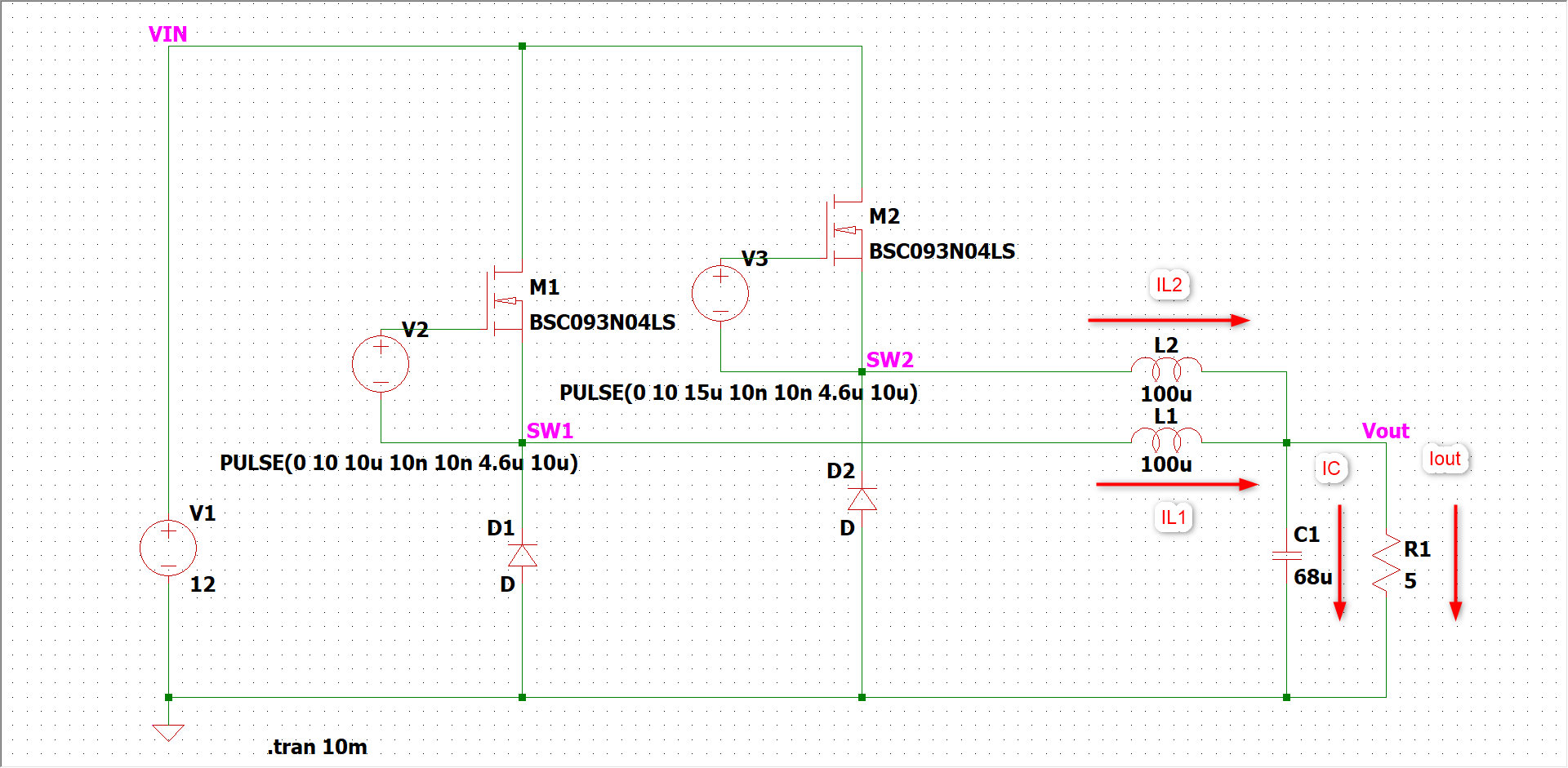
お疲れ様です。本記事はタイトル通り「インターリーブ運転するとなぜ出力リップル電圧が小さくなるのか?」を解説してみようと思います。
インターリーブ運転すると出力リップル電圧が小さくなるのはなんとなく理解しているけど、実は良く分かってない。
という方の参考になれば幸いです。
そもそもインターリーブ運転とは?
“インターリーブ(interleave)”の言葉の意味は”交互に扱う”とか”間に差しはさむ”という意味です。
パワエレにおいては出力コンデンサなどは共用にして、回路を複数並列に並べて位相をずらして同期動作させることを意味しています。
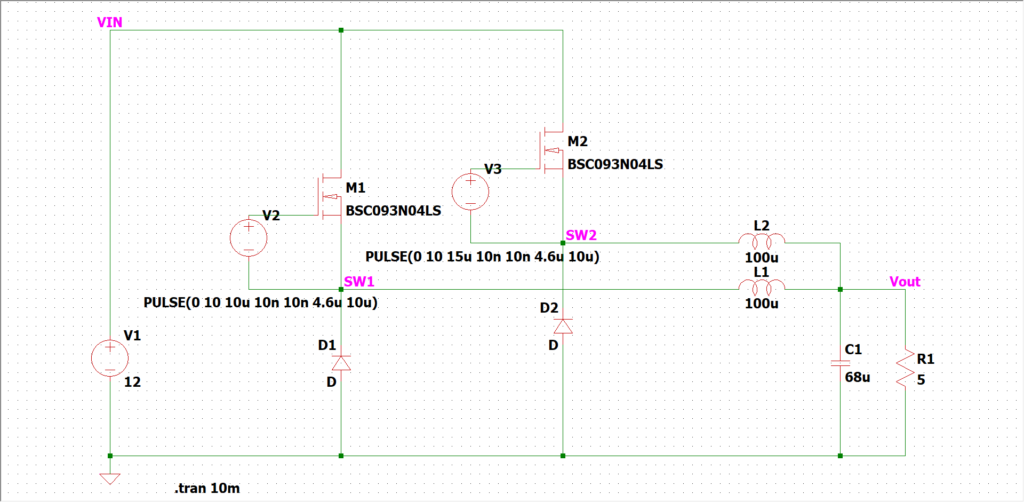
2並列であれば、180°ずらします。
3並列であれば、120°ずらします。
N並列であれば、360/N°ずらします。
動作波形のイメージは以下です。
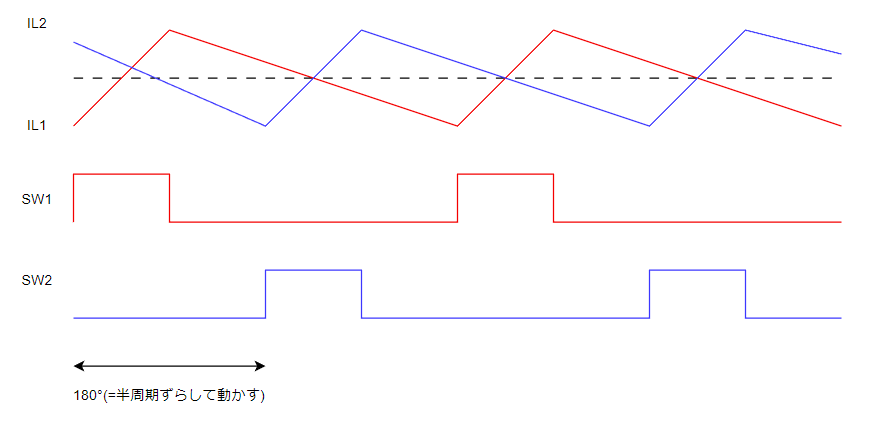
なんとなく「コイル電流がいい感じに打ち消されてリップル電圧が小さくなるんですよ。」と言われたら「あぁ、そんなもんか。」と納得できそうな感じです。
リップル低減効果のイメージ的解説
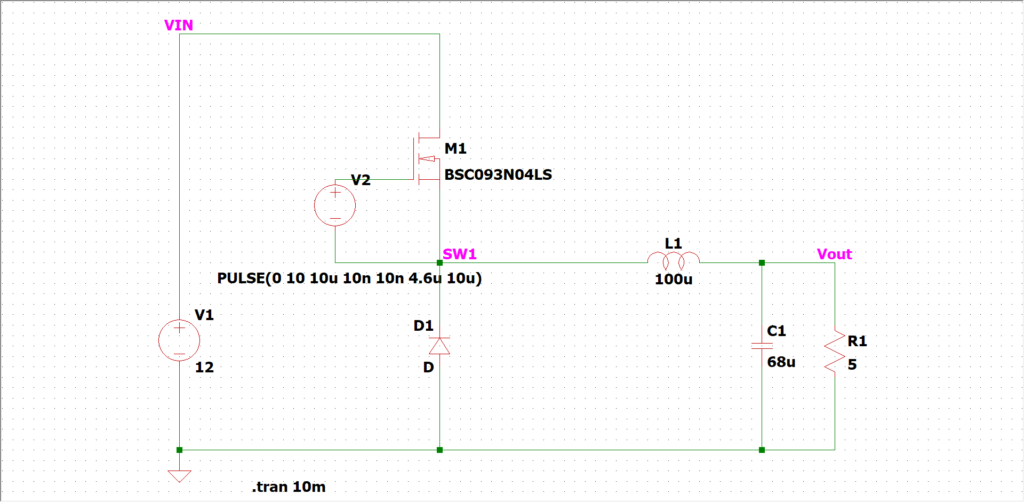
ざっくり解説してみようと思います。ここでも簡単な2並列降圧チョッパー回路を例にします。
リップル電圧は結局出力コンデンサに出し入れされる電流量で決まります。
インターリーブなしの単相の場合、コイルリップル電流がそのまま出力コンデンサに出たり入ったりします。
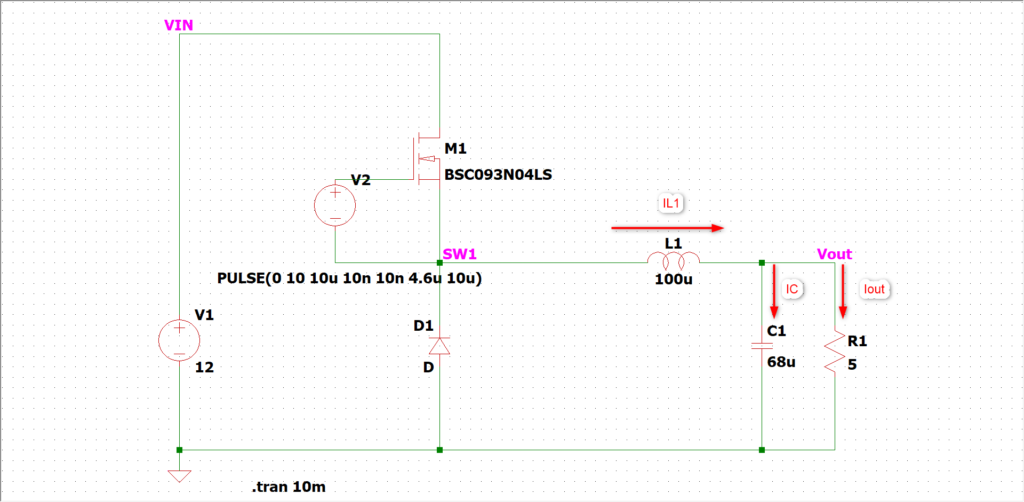
$$\small{
I_{L}=I_{C}+I_{out}
}$$
DC成分を除去したらこうですね↓。
$$\small{
ΔI_{L}=I_{C}
}$$
それに対して2並列インターリーブの場合はL1とL2合算が出力側に流れます。(単純にキルヒホッフの法則ですね。)
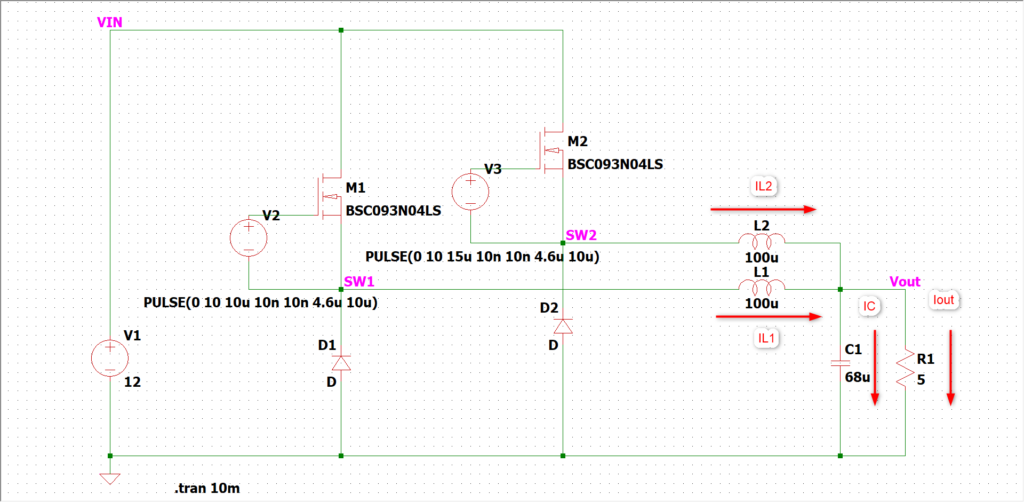
$$\small{
I_{L1}+I_{L2}=I_{C}+I_{out}
}$$
DC成分を除去したらこうですね↓。
$$\small{
ΔI_{L1}+ΔI_{L2}=I_{C}
}$$
ってことは以下画像のリップルで打ち消された残りがコンデンサに出たり入ったりします。

なので、リップル電圧が小さくなるんですね。まぁ結局はコンデンサに出し入れする電流が小さくなるから電圧が小さくなる。ってことです。
リップル低減効果の理論的解説
では数式的に“インターリーブ運転したらリップルは結局どれだけ小さくなるの?”を解説してみようと思います。ここでも簡単な2並列降圧チョッパー回路を例にします。
Duty≦50%のとき
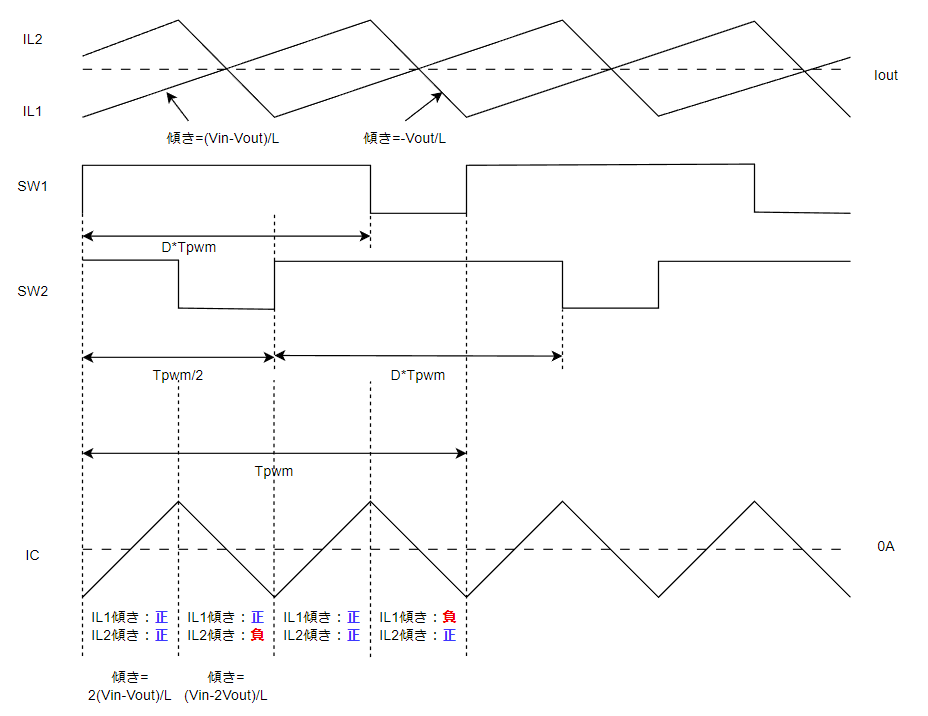
詳細の動作波形イメージ図を以下に示します。
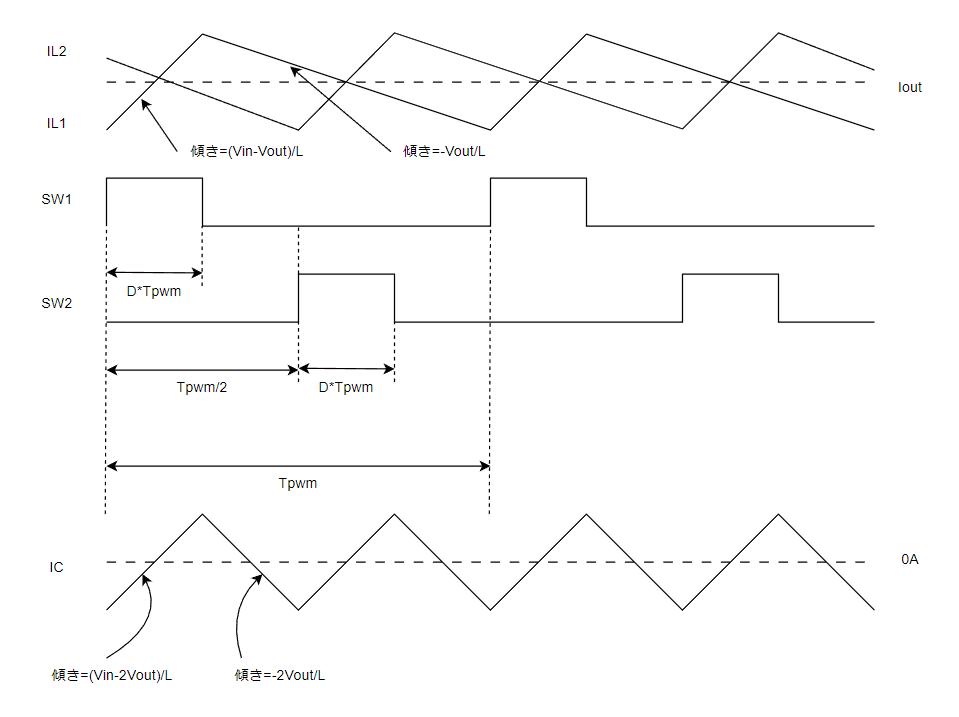
L1,L2のON/OFF時のリップル電流は以下の通りです。
$$\small{
ΔIL_{ON}=\frac{V_{in}-V_{out}}{L}*DT_{PWM}\\
ΔIL_{OFF}=\frac{-V_{out}}{L}*(1-D)T_{PWM}
}$$
最初の半周期(Tpwm/2)に注目して、ΔIL1とΔIL2を合成したらどうなるかを考えます。
最初のDTpwm間はΔIL1は上昇、ΔIL2は下降しています。このときの傾きは上記のON時とOFF時の傾きの足し算となります。
$$\small{
I_Cの傾き_①=\frac{V_{in}-V_{out}}{L}+\frac{-V_{out}}{L}=\frac{V_{in}-2V_{out}}{L}
}$$
あとの時間(Tpwm/2 – DTpwm)はΔIL1は下降、ΔIL2は下降しています。このときの傾きも上記のOFF時とOFF時の傾きの足し算となります。
$$\small{
I_Cの傾き_②=\frac{-V_{out}}{L}+\frac{-V_{out}}{L}=\frac{-2V_{out}}{L}
}$$
それぞれに時間をかけるとリップル電流となりますので、
$$\small{
IC_1=\frac{V_{in}-2V_{out}}{L}*DT_{pwm} \\
IC_2=\frac{-2V_{out}}{L}*(\frac{T_{pwm}}{2}-DT_{pwm})
}$$
出力電圧一定なので、IC1+IC2=0となります。
低減効果を確認するためにインターリーブなしのときとの比を計算します。
$$\small{
\frac{IC_{interleaved}}{IC}=\frac{\frac{V_{in}-2V_{out}}{L}*DT_{pwm}}{\frac{V_{in}-V_{out}}{L}*DT_{PWM}}
}$$
これを整理すると、以下の通りです。
$$\small{
\frac{ΔIC_{interleaved}}{ΔIC}=\frac{1-2D}{1-D}
}$$
D:Duty比
となります。これがDuty≦50%のときのリップル電流低減効果を表す式です。
50%≦Duty≦100%のとき
詳細の動作波形イメージ図は以下の通りです。
同様に最初の半周期Tpwm/2に注目して、ΔIL1とΔIL2を合成したらどうなるかを考えます。
最初はIL1,IL2ともに上昇していってます。
$$\small{
I_Cの傾き_①=\frac{V_{in}-V_{out}}{L}+\frac{V_{in}-V_{out}}{L}=\frac{2(V_{in}-V_{out})}{L}
}$$
次はΔIL1は上昇、ΔIL2は下降しています。
$$\small{
I_Cの傾き_②=\frac{V_{in}-V_{out}}{L}+\frac{-V_{out}}{L}=\frac{V_{in}-2V_{out}}{L}
}$$
それぞれに時間をかけるとリップル電流となりますので、
$$\small{
IC_1=\frac{2(V_{in}-V_{out})}{L}*(\frac{T_{pwm}}{2}-(1-D)T_{pwm}) \\
IC_2=\frac{V_{in}-2V_{out}}{L}*(1-D)T_{pwm}
}$$
出力電圧一定なので、IC1+IC2=0となります。
低減効果を確認するためにインターリーブなしのときとの比を計算します。
$$\small{
\frac{IC_{interleaved}}{IC}=\frac{\frac{2(V_{in}-V_{out})}{L}*(\frac{T_{pwm}}{2}-(1-D)T_{pwm})}{\frac{V_{in}-V_{out}}{L}*DT_{PWM}}
}$$
これを整理すると、以下の通りです。
$$\small{
\frac{IC_{interleaved}}{IC}=\frac{2D-1}{D}
}$$
理論式と低減効果のグラフ
2並列インターリーブ降圧チョッパー回路のリップル低減効果の理論式をまとめると以下の通りです。
Duty≦50%のとき
$$\small{
\frac{ΔIC_{interleaved}}{ΔIC}=\frac{1-2D}{1-D}
}$$
Duty>50%のとき
$$\small{
\frac{IC_{interleaved}}{IC}=\frac{2D-1}{D}
}$$
これをグラフにすると以下の通りとなります。
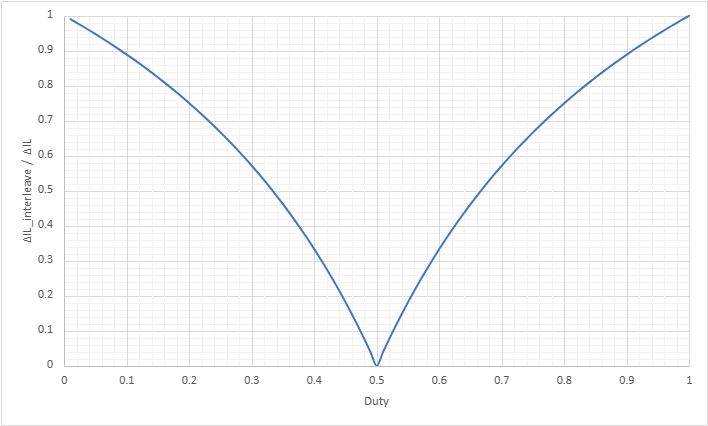
縦軸は”インターリーブありΔIC”と”インターリーブなしΔIC”の比です。小さいほどリップル低減効果が大きいです。
横軸はDutyです。
Dutyが50%付近になるとリップル低減効果が大きくなっています。
3並列や4並列はややこしいそうなので、もうやめておきます。
はい、本記事は以上です。何かの参考になれば幸いです。
最後までお読みいただきありがとうございました!!