みなさま、お疲れ様です。
本記事ではHブリッジ型多機能DCDCの動作原理について解説します。
Hブリッジ型多機能DCDCの動きがわからない!!
とお悩みの方の参考になれば幸いです。
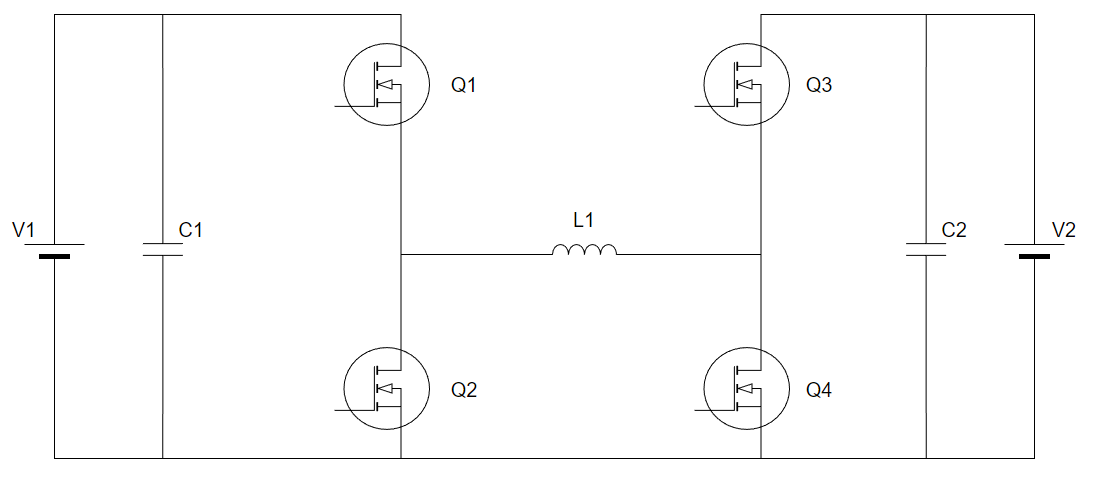
Hブリッジ型多機能DCDCの回路図は以下の通りです。
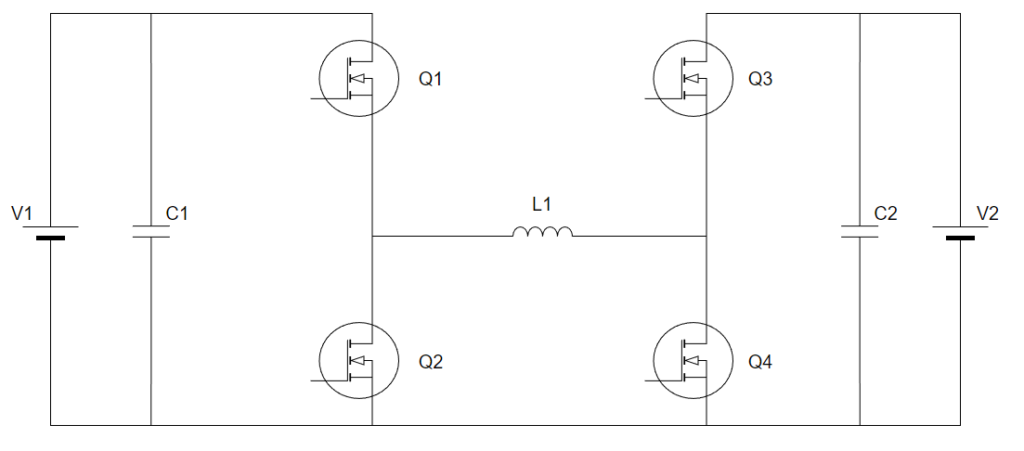
これで降圧、昇圧、昇降圧を行うことができます。便利ですね。双方向動作できますが、今回はV1⇒V2の方向について解説します。
先に結論を言ってしまえば、以下の計算式で動作します。
| モード | 入出力電圧関係式 |
|---|---|
| 降圧モード | $$\small{ V_2=D_1V_1 }$$ |
| 昇降圧モード | $$\small{ V_2=\frac{D_1}{D_2}V_1 }$$ |
| 昇圧モード | $$\small{ V_2=\frac{1}{1-D_2}V_1 }$$ |
※D1はQ1のON Duty幅。D2はQ4のON Duty幅。
それぞれのモードの動作について解説していきます。
降圧モード
降圧モードの動作モードは以下の2種類です。
| モード | Q1 | Q2 | Q3 | Q4 |
|---|---|---|---|---|
| 1 | ON | OFF | ON | OFF |
| 2 | OFF | ON | ON | OFF |
降圧モードではQ3は常にON、Q4は常にOFFで動作します。
動作モードと電流経路
モード1:Q1がON、Q2がOFF
電流経路は以下の通りです。

リアクトル電流は以下の通りです。
$$\small{
ΔI_{L1}=\frac{V_1-V_2}{L}T_1
}$$
非絶縁降圧DCDCのH-sideがONしたときと同じですね。
モード2:Q1がOFF、Q2がON
電流経路は以下の通りです。
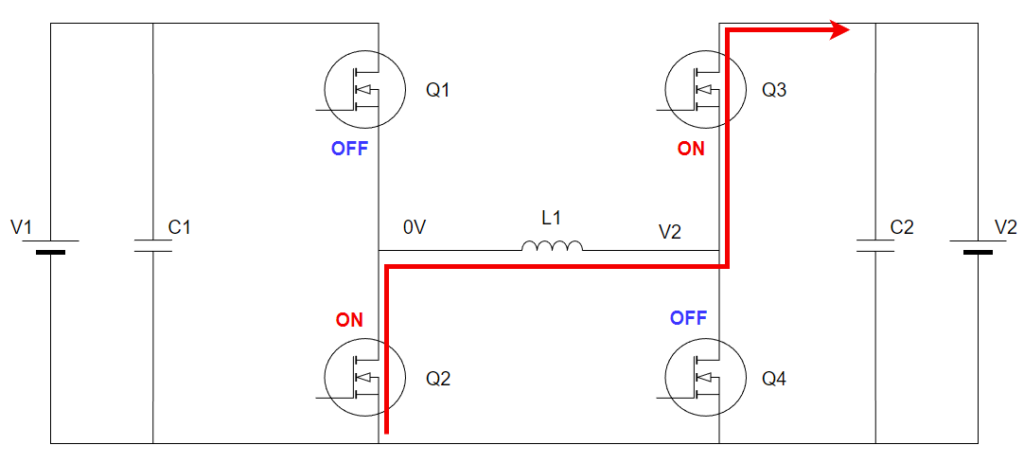
リアクトルの電流を流し続けようとする作用により、Q2から電流が流れます。
リアクトル電流は以下の通りです。
$$\small{
ΔI_{L2}=\frac{-V_2}{L}T_2
}$$
非絶縁降圧DCDCのL-sideがONしたときと同じですね。
入出力関係式
入力電圧と出力電圧の関係式を導出します。
「一周期のリアクトル電流を足し合わせると0になる。」のでそこから式を立てて解いて行きます。
$$\small{
ΔI_{L1}+ΔI_{L2}=0\\
\frac{V_1-V_2}{L}T_1+\frac{-V_2}{L}T_2=0
}$$
Q1がONしている割合をD1、Q2がONしている割合を1-D1として、一周期をTpwmとします。
すると、T1=D1*Tpwm、T2=(1-D1)*Tpwmと表現できます。
それを代入します。
$$\small{
\frac{V_1-V_2}{L}D_1T_{PWM}+\frac{-V_2}{L}(1-D_1)T_{PWM}=0
}$$
LとTpwmを消します。
$$\small{
(V_1-V_2)D_1-V_2(1-D_1)=0
}$$
上の式を整理すると以下の通りです。
$$\small{
V_2=D_1V_1
}$$
お馴染みの降圧DCDCの式が出てきました。これが降圧モードの入出力電圧関係式となります。
昇圧モード
昇圧モードの動作モードは以下の2種類です。
| モード | Q1 | Q2 | Q3 | Q4 |
|---|---|---|---|---|
| 1 | ON | OFF | OFF | ON |
| 2 | ON | OFF | ON | OFF |
昇圧モードではQ1は常にON、Q2は常にOFFで動作します。
動作モードと電流経路
モード1:Q3がOFF、Q4がON
電流経路は以下の通りです。
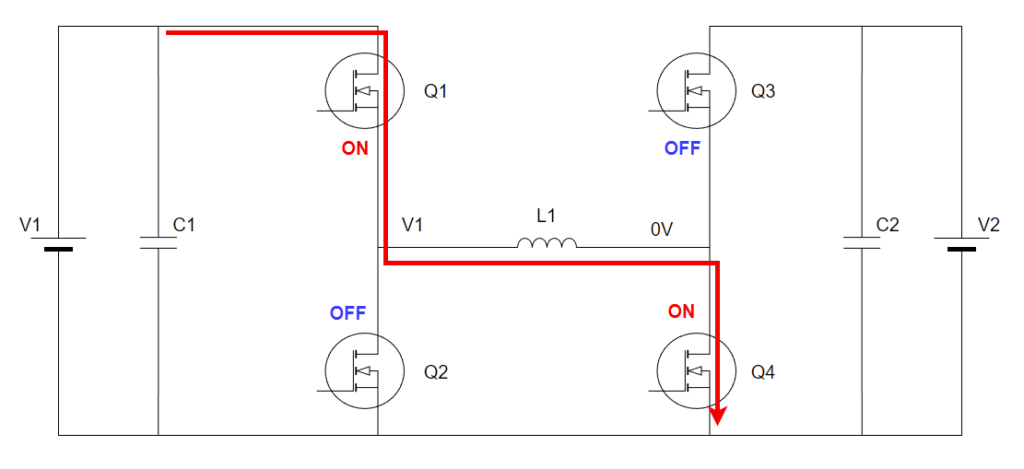
昇圧DCDCのチャージのときの動作ですね。
リアクトル電流は以下の通りです。
$$\small{
ΔI_{L1}=\frac{V_1}{L}T_1
}$$
モード2:Q3がON、Q4がOFF
電流経路は以下の通りです。
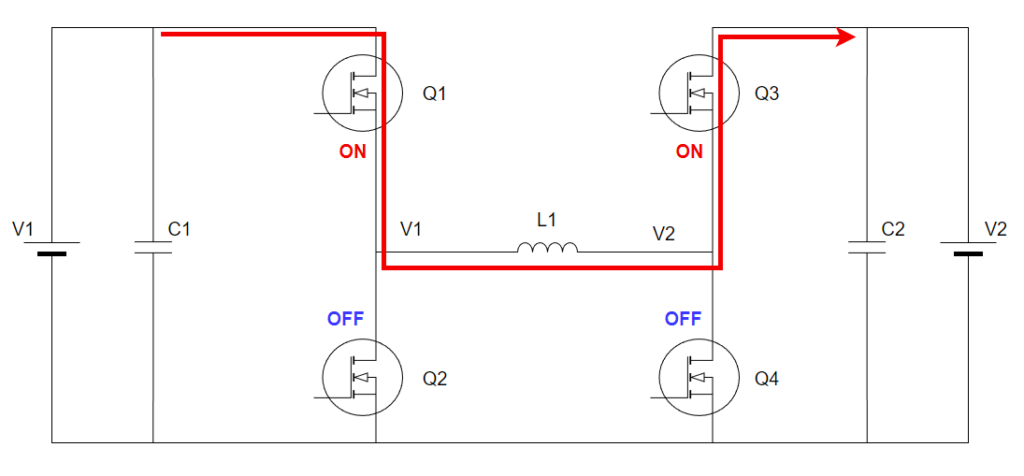
リアクトルの電流を流し続けようとする作用により、Q3へ電流が流れます。
昇圧DCDCのディスチャージのときの動作ですね。
リアクトル電流は以下の通りです。
$$\small{
ΔI_{L2}=\frac{V_1-V_2}{L}T_2
}$$
入出力関係式
降圧と同様に「一周期のリアクトル電流を足し合わせると0になる。」のでそこから式を立てて解いて行きます。
$$\small{
ΔI_{L1}+ΔI_{L2}=0\\
\frac{V_1}{L}T_1+\frac{V_1-V_2}{L}T_2=0
}$$
Q4がONしている割合をD2、Q3がONしている割合を1-D2として、一周期をTpwmとします。
すると、T1=D2*Tpwm、T2=(1-D2)*Tpwmと表現できます。
それを代入します。
$$\small{
\frac{V_1}{L}D_2T_{PWM}+\frac{V_1-V_2}{L}(1-D_2)T_{PWM}=0
}$$
LとTpwmを消します。
$$\small{
V_1D_2+(V_1-V_2)(1-D_2)=0
}$$
上の式を整理すると以下の通りです。
$$\small{
V_2=\frac{1}{1-D_2}V_1
}$$
お馴染みの昇圧DCDCの式が出てきました。これが昇圧モードの入出力電圧関係式となります。
昇降圧モード
昇降圧モードではQ1~Q4のスイッチがON/OFFします。
| モード | Q1 | Q2 | Q3 | Q4 |
|---|---|---|---|---|
| 1 | ON | OFF | ON | OFF |
| 2-1 | OFF | ON | ON | OFF |
| 2-2 | ON | OFF | OFF | ON |
| 3 | OFF | ON | OFF | ON |
Q1のONタイミングとQ4のONタイミングを同期していた場合、
モード1⇒モード2-1⇒モード3
モード1⇒モード2-2⇒モード3
のどちらかで動作します。いずれにしても入出力電圧関係式は同じになります。
動作モードと電流経路
モード1:Q1,Q3がON
電流経路は以下の通りです。

リアクトル電流は以下の通りです。
$$\small{
ΔI_{L1}=\frac{V_1-V_2}{L}T_1
}$$
モード2-1:Q2,Q3がON
電流経路は以下の通りです。

リアクトル電流は以下の通りです。
$$\small{
ΔI_{L2-1}=\frac{-V_2}{L}T_{2-1}
}$$
モード2-2:Q1,Q4がON
電流経路は以下の通りです。

リアクトル電流は以下の通りです。
$$\small{
ΔI_{L2-2}=\frac{V_1}{L}T_{2-2}
}$$
モード3:Q2,Q4がON
電流経路は以下の通りです。
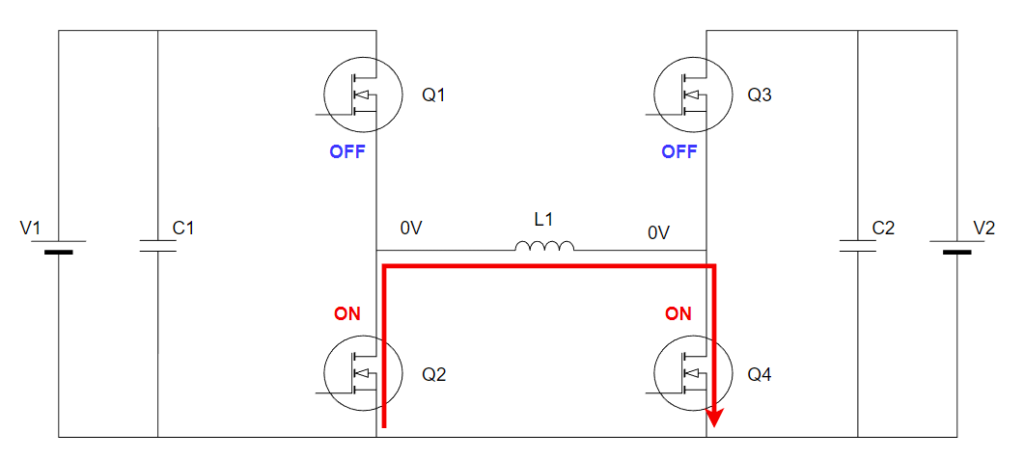
リアクトル電流は以下の通りです。
$$\small{
ΔI_{L3}=\frac{0V}{L}T_{3}=0
}$$
このモードだけ増減は0Aとなります。
入出力関係式
まずは、”モード1⇒モード2-1⇒モード3″となる場合を考えます。
今までと同様に一周期のリアクトル電流は0になるので、
$$\small{
ΔI_{L1}+ΔI_{L2-1}+ΔI_{L3}=0\\
\frac{V_1-V_2}{L}T_1+\frac{-V_2}{L}T_{2-1}=0
}$$
モード3の電流は0なので、省略です。
T1はD1*Tpwmと表現できます。
T2_1は(D2-D1)Tpwmと表現できます。
それらを代入して、LとTpwmを消します。
$$\small{
(V_1-V_2)D_1-V_2(D_2-D_1)=0
}$$
これを整理すると
$$\small{
V_2=\frac{D_1}{D_2}V_1
}$$
となります。
つづいて”モード1⇒モード2-2⇒モード3″となる場合を考えます。
今までと同様に一周期のリアクトル電流は0になるので、
$$\small{
ΔI_{L1}+ΔI_{L2-2}+ΔI_{L3}=0\\
\frac{V_1-V_2}{L}T_1+\frac{V_1}{L}T_{2-2}=0
}$$
モード3の電流は0なので、省略です。
T1はD2*Tpwmと表現できます。
T2_2は(D1-D2)Tpwmと表現できます。
それらを代入して、LとTpwmを消します。
$$\small{
(V_1-V_2)D_2+V_1(D_1-D_2)=0
}$$
これを整理すると
$$\small{
V_2=\frac{D_1}{D_2}V_1
}$$
となります。
結局同じ式が出てきました。
PWM波形の実現方法
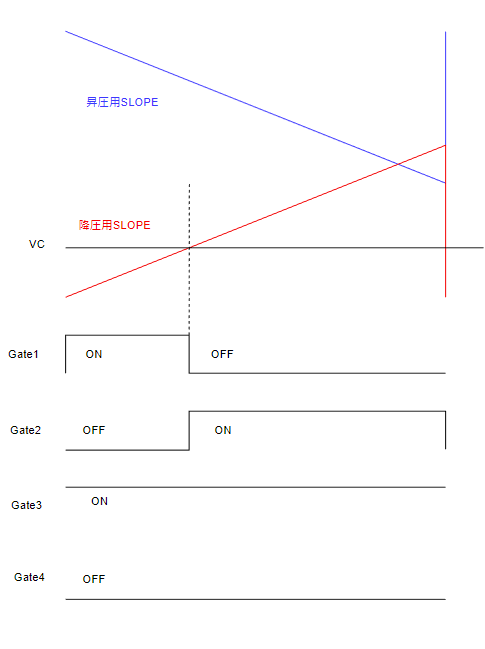
PWM波形は以下のように作ります。

このようにすることで、VC電圧の位置によって降圧/昇降圧/昇圧を切り替えることが出来ます。
1周期の動作波形イメージ図は以下の通りです。

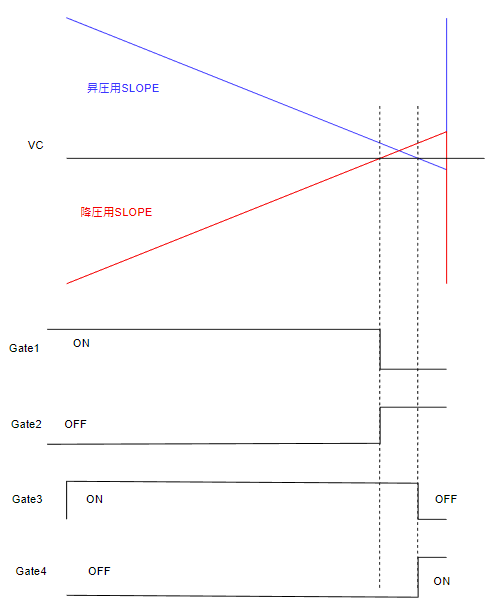
シミュレーションでの動作確認
「はいはい、そういう動作原理だと君が思ってるってことはわかったよ。でもそれだけだと”僕を信じて下さい。”としか言ってないよね。証拠を提示してくださいよ。証拠を。」
という方に向けて、PSIMでシミュレーションをした結果を示します。PSIMの導入方法はこちらの記事で解説しておりますので、良かったら読んでみて下さい。
まず回路は以下の通りです。

シミュレーション結果は以下の通りです。
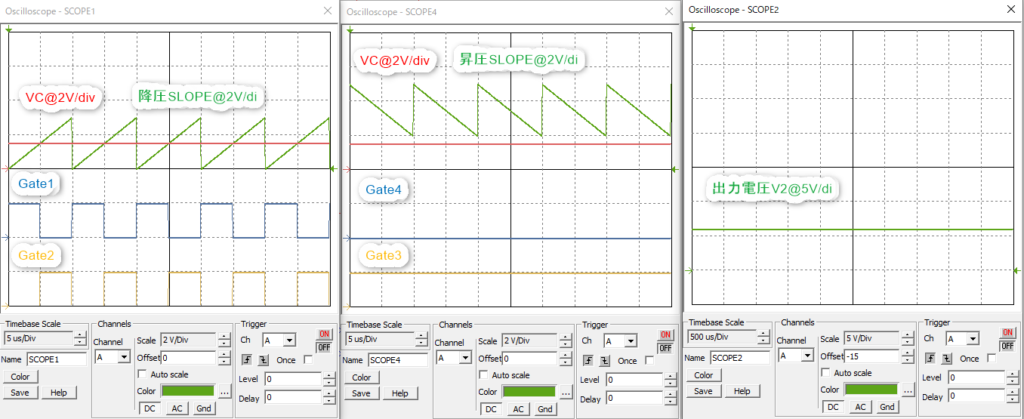
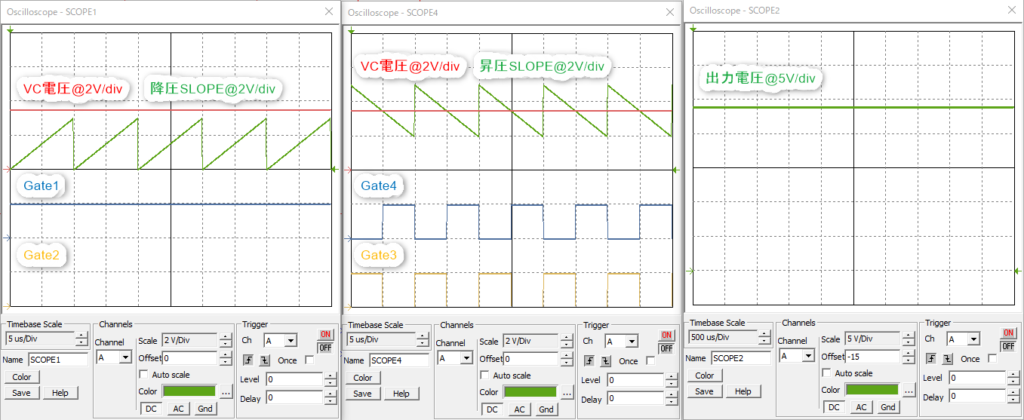
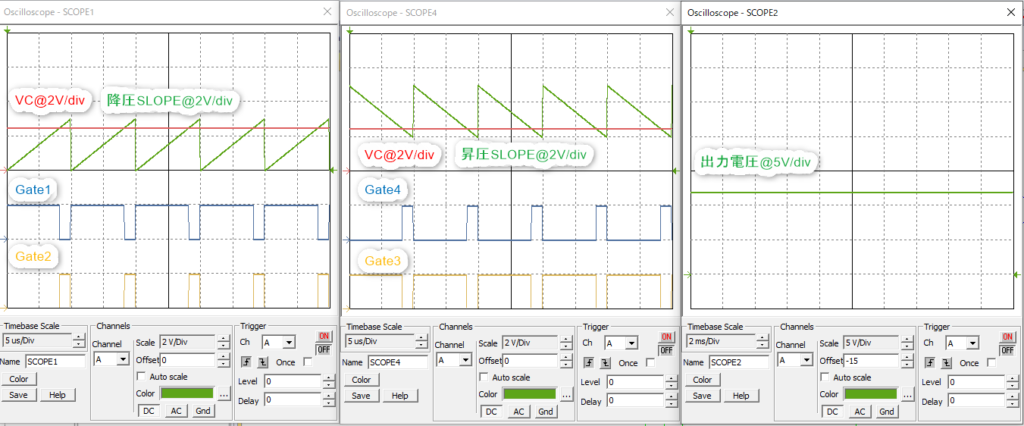
想定通りに動作しており、問題ないです。
はい、本記事は以上となります。誰かの参考になれば幸いです。最後までお読みいただきありがとうございました!!