2段オペアンプ↓の設計方法を解説してみようという試みの記事の2回目です。
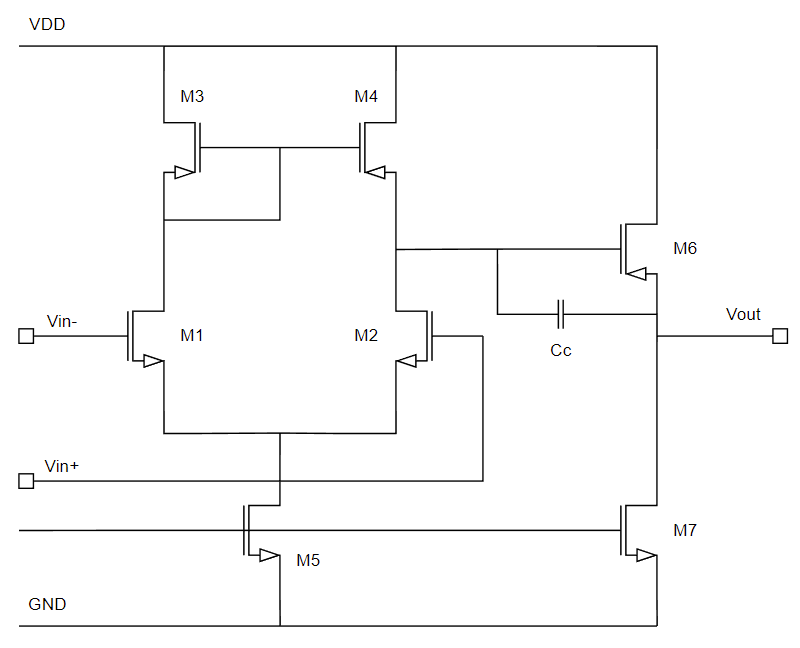
今回は前回記事で書き直した小信号等価回路を使って、オペアンプの周波数特性を計算してみようと思います。
1回目:【2段オペアンプ設計方法】小信号等価回路化してDCゲインを計算してみる
2回目:【2段オペアンプの設計方法】周波数特性の計算をしてみる(本記事)
3回目:【2段オペアンプの設計方法】なぜ設計条件は(gm6=10gm1、Cc>0.2Cout)なのか?
本記事では
・谷口先生本のP189 「gm6=10gm1、Cc>0.2Cout」で挫折しました。
・なーにが「これがミラー補償法に基づくOPアンプを設計する際の制約条件なのです。」だ!さっぱりわからんぞ!!!!!
という超ピンポイントの悩みをお持ちの方へ解決となれば、非常に嬉しいです。
ちなみに本記事は周波数特性を導くまでの記事です。
そっから谷口先生本の「gm6=10gm1、Cc>0.2Cout」を求めるのは次回にしたいと思います。(周波数特性を導くまでが長かったので。。。)
では、本記事を始めます。
まず小信号等価回路を作れていないとスタートできない
小信号等価回路は以下のようになります↓。
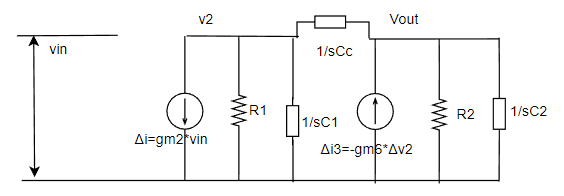
$$R1=ro2//ro4$$
$$R2=ro6//ro7$$
何でこうなるの?という方は前回記事で解説しているので良かったらそちらを参照ください。
これがないと計算を始めることが出来ません。
キルヒホッフの法則を使って式をたてる
計算の前に電流源の方向を下向きに統一しました。(i3の方向を下側にしました。)
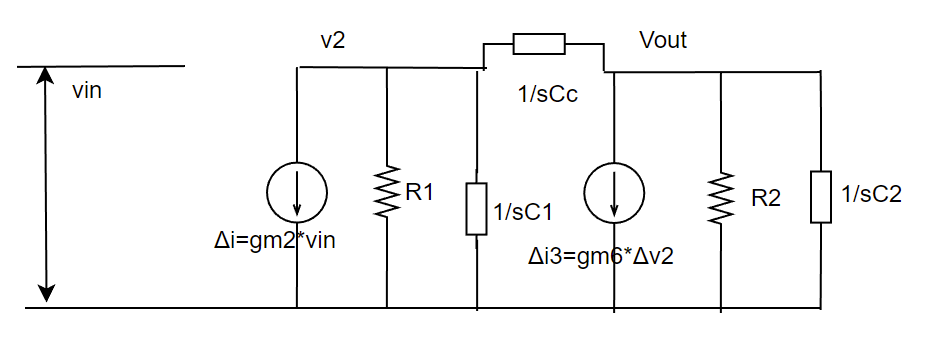
(Vout->V2方向へ流れる電流)=(左側の電流の合計)となるので、その通りに式を立てます。
$$\frac{vout-v2}{\frac{1}{sCc}}=gm2*vin+\frac{v2}{R1}+\frac{v2}{\frac{1}{sC1}}$$
整理します↓。
$$(vout-v2)sCc=gm2*vin+\frac{v2}{R1}+v2*sC1$$
次に(V2->Vout方向へ流れる電流)=(右側の電流の合計)となるので、その通りに式を立てます。
$$\frac{vout-v2}{\frac{1}{sCc}}=gm6*v2+\frac{vout}{R2}+\frac{vout}{\frac{1}{sC2}}$$
整理します↓。
$$(v2-Vout)sCc=gm6*v2+\frac{vout}{R2}+vo*sC2$$
はい、まとめると以下の2式が立式できました。
$$\begin{cases}
(vout-v2)sCc=gm2*vin+\frac{v2}{R1}+v2*sC1\\
(v2-Vout)sCc=gm6*v2+\frac{vout}{R2}+vo*sC2\\
\end{cases}$$
式がvo/vin=~となるように解いて行く
↑の式がvo/vin=~となるように解いていく。といって「わかりました!」といって解いて行く人は社畜の才能ありです。
こんな単純な計算はパソコンにやってもらいましょう。私はPythonのsympyを使って解いて行きました。pythonで解いた記事も後日書いてみます。
まぁとりあえず計算結果は以下の式になります。
$$\frac{vout}{vin}=\frac{R1R2gm2(Ccs-gm6)}{CcR1R2s(Ccs-gm6)-(C1R1s+CcR1s+1)(CcR2s+C2R2s+1)}$$
DCゲインは
$$Av=R1R2gm2gm6$$
なので
$$\frac{vout}{vin}=\frac{Av(\frac{Cc}{gm6}s-1)}{CcR1R2s(Ccs-gm6)-(C1R1s+CcR1s+1)(CcR2s+C2R2s+1)}$$
はい。これでvout/vinが計算できました。
次はここから分母をガシガシ計算してポール周波数を考えます。
式を周波数特性が分かる様に整理する
まずこの式↓ですが、念のためs=0のときにDCゲインだけが残るかをチェックします。
$$\frac{vout}{vin}=\frac{Av(\frac{Cc}{gm6}s-1)}{CcR1R2s(Ccs-gm6)-(C1R1s+CcR1s+1)(CcR2s+C2R2s+1)}$$
s=0を入れましょう。
$$\frac{vout}{vin}=\frac{Av(\frac{Cc}{gm6}*0-1)}{CcR1R2*0*(Cc*0-gm6)-(C1R1*0+CcR1*0+1)(CcR2*0+C2R2*0+1)}$$
0を消しましょう。
$$\frac{vout}{vin}=\frac{-Av}{-(1)(1)}=Av$$
うん。いいですね。ちゃんとDCゲインだけが残っています。
$$Av=R1R2gm2gm6$$
さて、次に分子に注目します。
$$\frac{vout}{vin}=\frac{Av(\frac{Cc}{gm6}s-1)}{CcR1R2s(Ccs-gm6)-(C1R1s+CcR1s+1)(CcR2s+C2R2s+1)}$$
これからもうゼロ点周波数は明らかです。分子の根がゼロ点周波数です。
$$z=\frac{gm6}{Cc}$$
さて、嫌々ながら分母を計算していきます。
その前に分子分母に”-1″を掛けときます。そしたら後で負が少なくなって楽です。
$$\frac{vout}{vin}=\frac{Av(1-\frac{Cc}{gm6}s)}{-CcR1R2s(Ccs-gm6)+(C1R1s+CcR1s+1)(CcR2s+C2R2s+1)}$$
分母を展開していい感じ1,s,s^2にまとめます。
$$分母=1+s(R1(C1+C2)+R2(C2+Cc)+gm6R1R2Cc)+s^2(R1R2(C1C2+CcC1+CcC2))$$
はい。ここでよくやるやつをやります。因数分解できたと仮定するパターンです。
以下のようにP1,P2を使って因数分解が出来たと仮定します。
$$(1-\frac{s}{p1})(1-\frac{s}{p2})$$
これを展開すると
$$(1-\frac{s}{p1})(1-\frac{s}{p2})=1-s(\frac{1}{p1}+\frac{1}{p2})+s^2\frac{1}{p1p2}$$
で、ですね。アナログ回路で良ーくやるやつ。経験的に|p2|>>|p1|なんですね。それを考慮すると1/p2とかゴミだよね。で簡略化します。
$$1-s(\frac{1}{p1}+\frac{1}{p2})+s^2\frac{1}{p1p2}=1-s\frac{1}{p1}+s^2\frac{1}{p1p2}$$
すると、前の式と比較して
$$p1=\frac{-1}{R1(C1+C2)+R2(C2+Cc)+gm6R1R2Cc}$$
となります。そんでですね。まーたやるんですが、gm6がくっそでかいじゃん。と。それに比べたらR1(C1+C2)とR2(C2+Cc)なんてゴミじゃん。と。無視します。したがって。
$$p1=\frac{-1}{gm6R1R2Cc}$$
これが2段オペアンプのポール周波数の一つです。
$$p1=\frac{-1}{gm6R1R2Cc}$$
あとはp2を解いて行きます。
$$p2=\frac{-(R1(C1+C2)+R2(C2+Cc)+gm6R1R2Cc)}{R1R2(C1C2+CcC1+CcC2)}$$
はい。分子を見ると、gm6がいますね。ということは、、、分かりますね。前半はゴミなので消します。
$$p2=\frac{-(gm6R1R2Cc)}{R1R2(C1C2+CcC1+CcC2)}$$
都合良いことにR1R2が分子分母にいるので、消します。
$$p2=\frac{-gm6Cc}{C1C2+CcC1+CcC2}$$
はい。ここでまた経験的にですね。C2>Cc>C1なんですねぇ。なので、いっちゃんでかいCcC2以外無視したらいいやん!って粗い感じに無視します。
アナログ回路は「高周波の領域はもう粗目でいいじゃん。どうせズレるし。」みたいな雰囲気があります。
$$p2=\frac{-gm6Cc}{CcC2}=\frac{-gm6}{C2}$$
はい、これがポールですね。
$$p2=\frac{-gm6}{C2}$$
あ~~~~疲れた。
一旦まとめ
さて、一旦まとめましょう。2段オペアンプの周波数特性のポイントをvout/vinから以下ように導出できます。
DCゲイン:$$Av=R1R2gm2gm6$$
ゼロ点周波数:$$z=\frac{gm6}{Cc}$$
ポール周波数①:$$p1=\frac{-1}{gm6R1R2Cc}$$
ポール周波数②:$$p2=\frac{-gm6}{C2}$$
最後にこれをボード線図に描くこうなります↓。
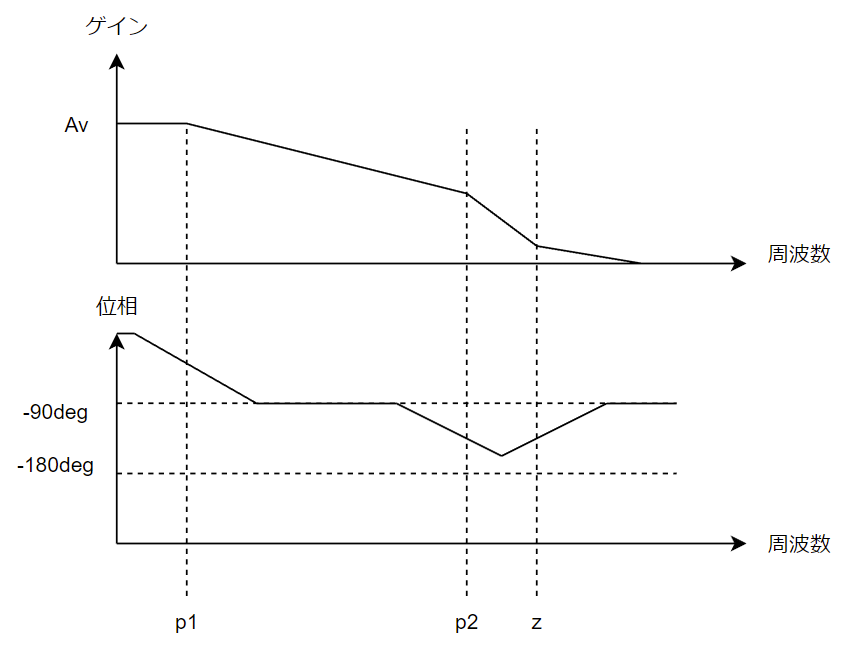
さて、この周波数特性を安定させるためにはどうしたらいいのか?を考えると谷口本の結果が導かれます。
そしてそれは次回とさせて頂きます。
いや、2段オペアンプむずすぎだろ!!!
最後までお読みいただきありがとうございました!!!何かの参考になれば幸いです!!!