みなさま、お疲れ様です。
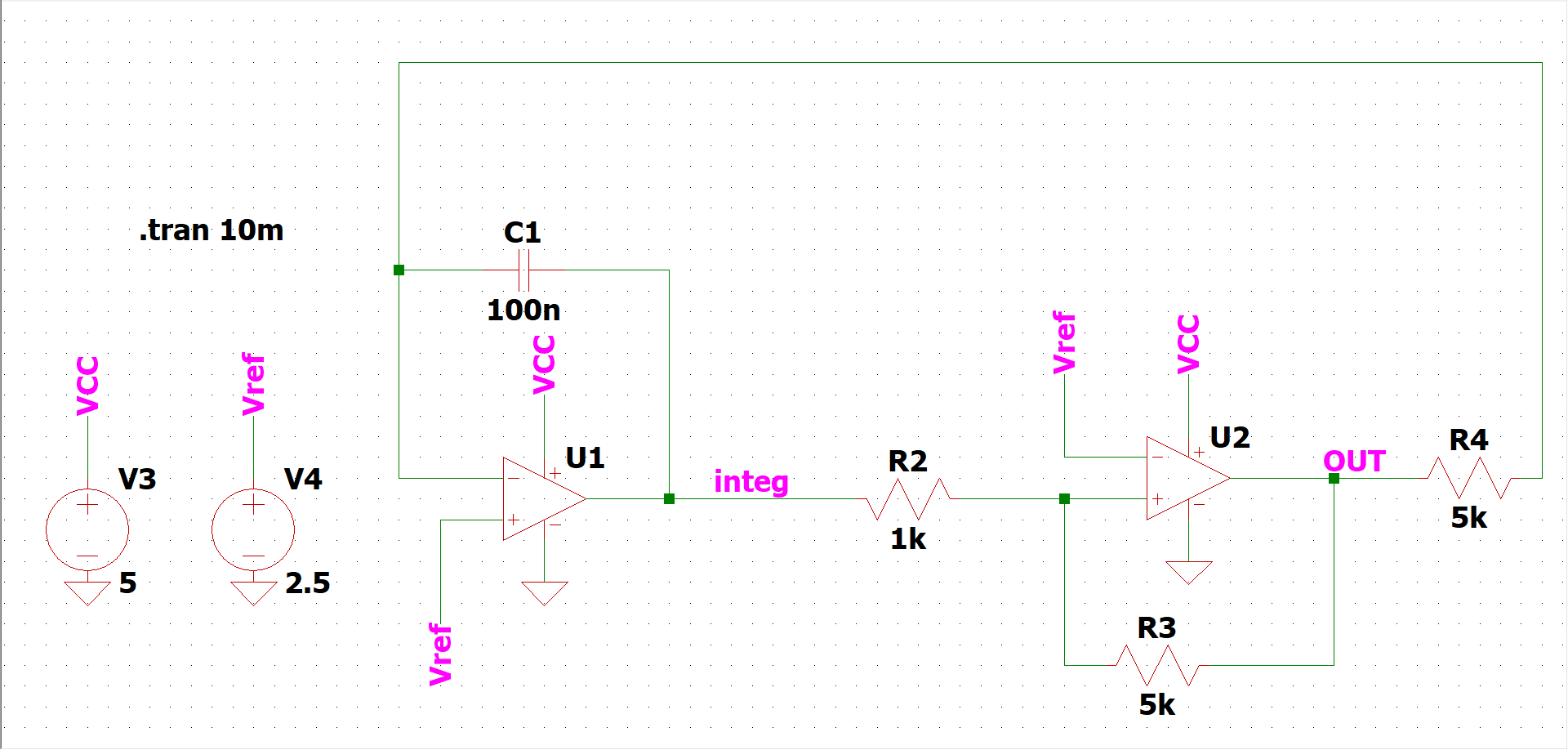
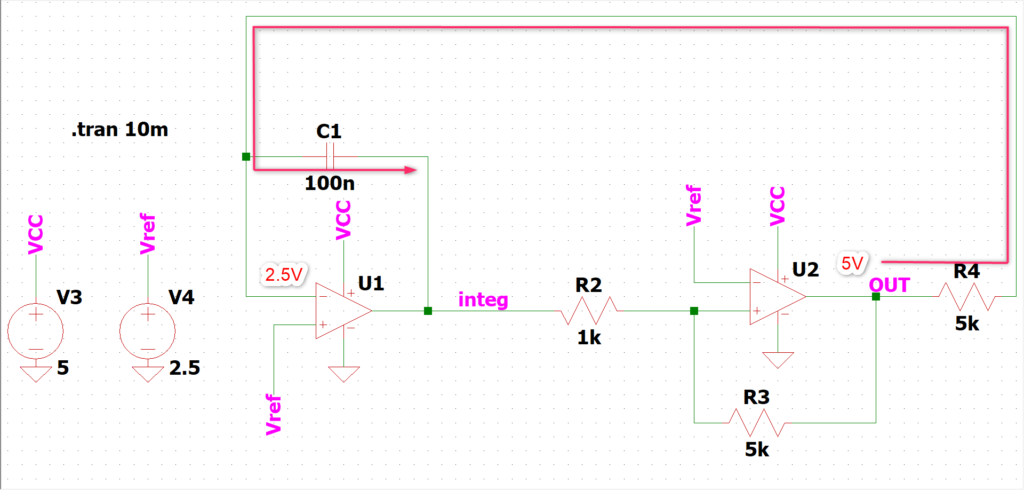
本日はこの回路↓を取り上げます。50%DUTYの矩形波を生成する回路です。
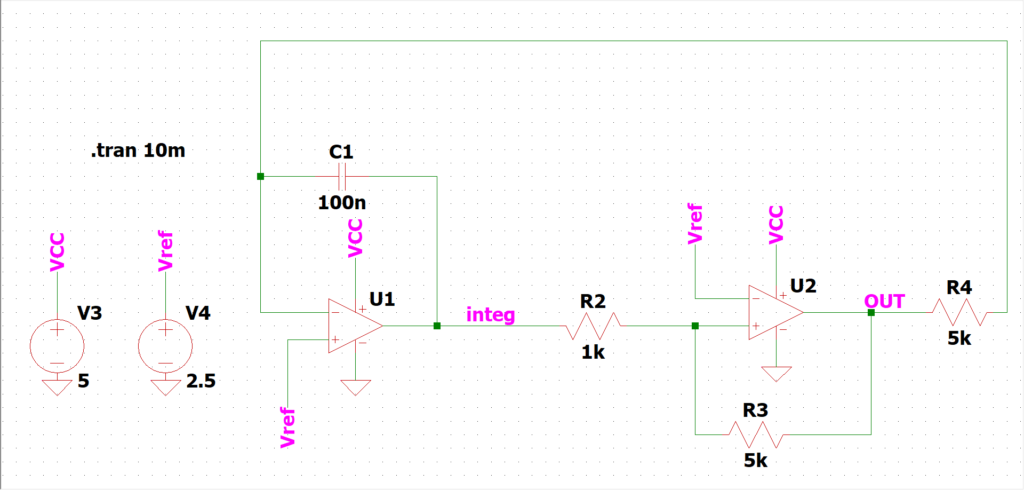
- 簡単な50%DUTYの矩形波生成回路が欲しい。
- この回路はどうやって動くのか?
という方の参考になれば幸いです。
回路の構成としては、U1の積分回路とU2のヒス付きコンパレータで実現しております。それぞれの回路については以下の記事で解説していますので、良ければ読んでみて下さい。
では、始めます。
どのように動くのか?
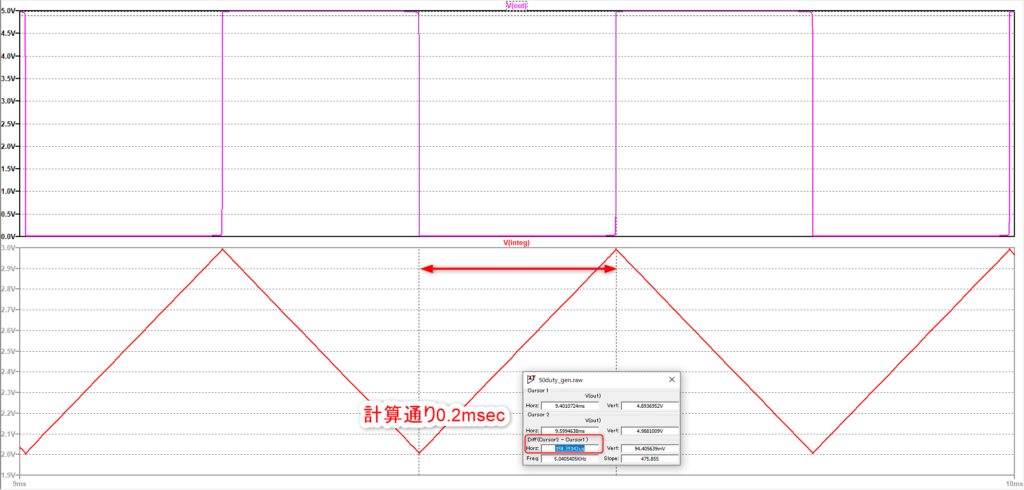
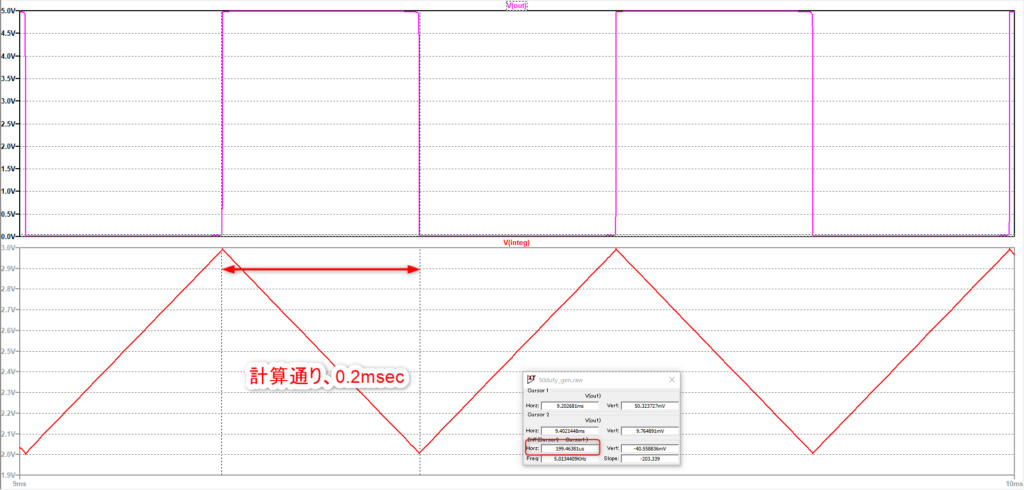
とりあえずこの回路のシミュレーション結果を示します。
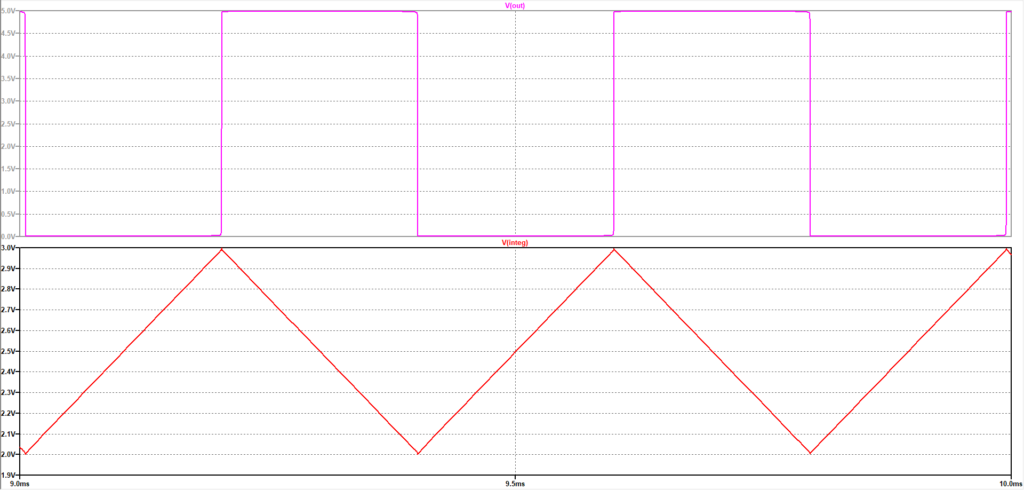
U2の出力電圧V(out)がこの回路のアウトプットです。50%Dutyの矩形波が出力されています。
U1の出力電圧V(integ)は積分回路の出力です。
この矩形波の周波数は以下の式で計算できます。
$$\small{
T=\frac{V_{integ}}{\frac{Vref-V_L}{R_4C_1}}+\frac{-V_{integ}}{\frac{Vref-V_H}{R_4C_1}}\\
f=\frac{1}{T}
}$$
Vinteg:積分範囲(ヒステリシス幅)[V]
Vref:基準電圧[V]
VL:Low時の出力電圧[V]
VH:High時の出力電圧[V]
T:周期[sec]
f:周波数[Hz]
では、なぜこのように動くのか?を解説してみます。
動作原理の説明
前提
まず要素回路のヒス付きコンパレータの動きを把握しておきましょう。このコンパレータの閾値は以下の式で計算できます。
HighからLowへの切り替わり閾値
$$\small{
V_{in}=V_{ref}+\frac{R_2}{R_3}(V_{ref}-V_H)
}$$
LowからHighへの切り替わり閾値
$$\small{
V_{in}=V_{ref}+\frac{R_2}{R_3}(V_{ref}-V_L)
}$$
Vin:入力電圧(=integ)[V]
Vref:基準電圧[V]
VL:Low時の出力電圧[V]
VH:High時の出力電圧[V]
詳細説明はこちらの記事を参照ください。
今回の例ではVref=2.5V、VL=0V、VH=5V、R2=1kΩ、R3=5kΩなので、以下の閾値で出力が切り替わります。
| HighからLow切り替わり閾値 | 2V |
| LowからHigh切り替わり閾値 | 3V |
つまりinteg電圧が3Vを超えるとHighへ、integ電圧が2Vを下回るとLowへ切り替わります。
コンパレータの出力電圧がLowのときとHighのときで分けて考えると動作が分かりやすいので、順番に説明します。
コンパレータ出力がLowのとき
まず、コンパレータ出力がLowのとき各ノードの電圧は以下のようになります。
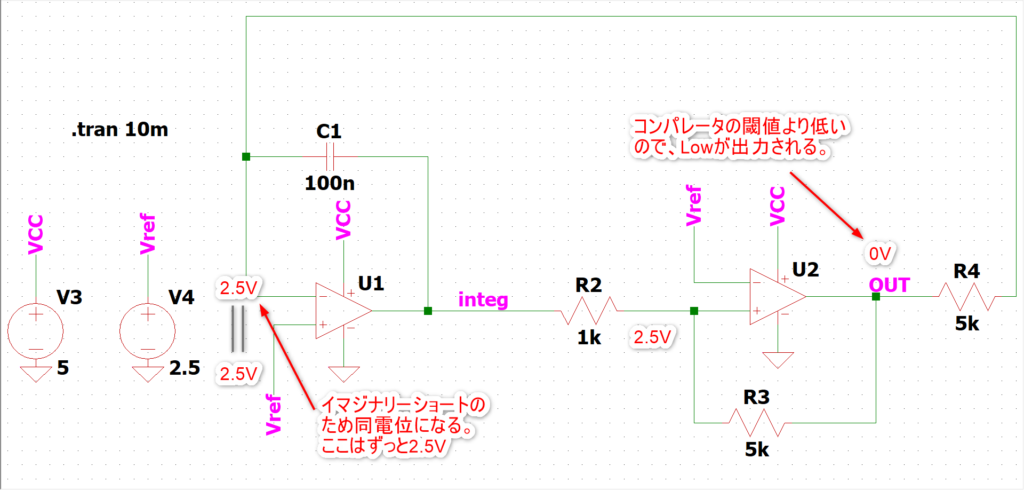
R4にかかる電圧は2.5Vと0Vなので2.5V/R4の定電流が流れます。経路は以下のような経路です。
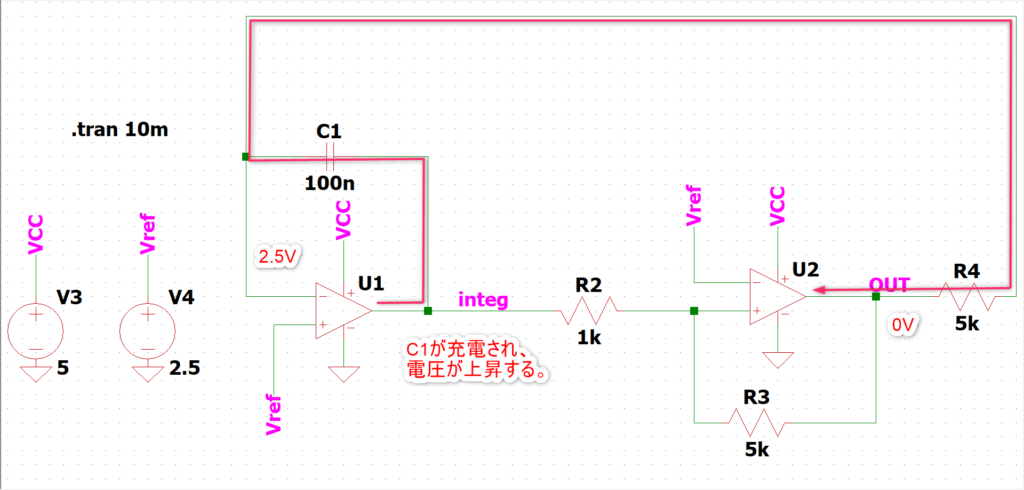
この定電流がC1に流れて充電されます。この電流値は以下の式で計算できます。
$$\small{\frac{Vref-V_L}{R_4}}$$
定電流でC1が充電されるので、integ電圧は一定のスピードで上昇します。電圧上昇スピードは以下の式で計算できます。
$$\small{
V_{integ}=\frac{Vref-V_L}{R_4C_1}*t
}$$
これが2Vから3Vに上昇したら、コンパレータ出力がLowからHighへ切り替わります。差分の1V上昇する時間はこの式をt=に変更したら求められます。
$$\small{
t=\frac{V_{integ}}{\frac{Vref-V_L}{R_4C_1}}
}$$
今回の例では
$$\small{
t=\frac{1V}{\frac{2.5-0}{5k100n}}=0.2[msec]
}$$
0.2msecですね。
次にコンパレータ出力がHighに切り替わったときの動作を解説します。
コンパレータ出力がHighのとき
integ電圧が3Vを超えたらコンパレータ出力がHighへ切り替わります。そのときの各ノードの電圧は以下のようになります。
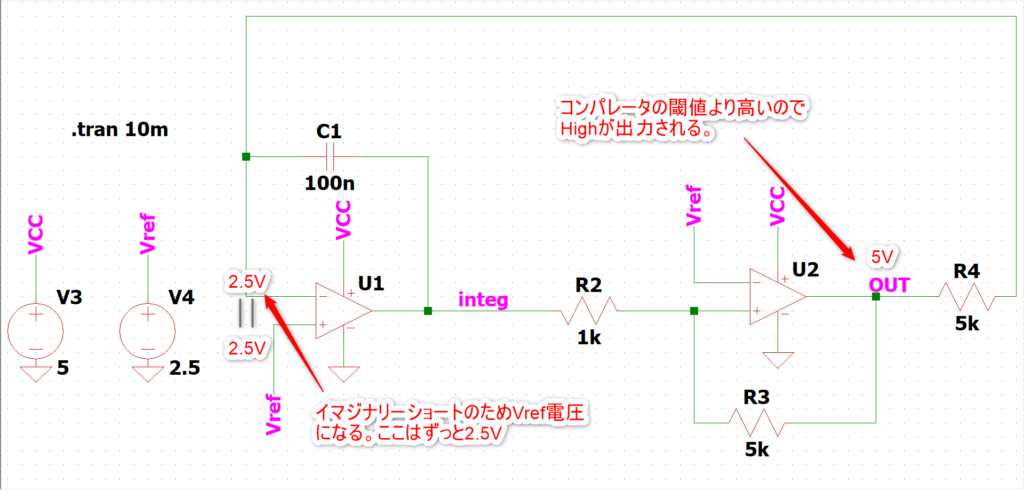
R4にかかる電圧は2.5Vと5Vなので5V-2.5V/R4の定電流が流れます。経路は以下のような経路です。Lowのときとは逆方向に同じ大きさの電流が流れます。
この定電流がC1に流れて放電されます。この電流値は以下の式で計算できます。
$$\small{\frac{Vref-V_H}{R_4}}$$
電流値はマイナスなので、先ほどとは逆方向になります。
あとは先ほどと同じです。定電流でC1が放電されるので、integ電圧は一定のスピードで減少します。電圧減少スピードは以下の式で計算できます。
$$\small{
V_{integ}=\frac{Vref-V_H}{R_4C_1}*t
}$$
これが3Vから2Vに減少したら、コンパレータ出力がHighからLowへ切り替わります。差分の-1V減少する時間はこの式をt=に変更したら求められます。
$$\small{
t=\frac{V_{integ}}{\frac{Vref-V_H}{R_4C_1}}
}$$
今回の例では
$$\small{
t=\frac{-1V}{\frac{2.5-5}{5k100n}}=0.2[msec]
}$$
0.2msecですね。
あとはまたコンパレータがLowに切り替わり、繰り返しです。
周波数の計算方法
充電時間+放電時間が一周期です。
$$\small{
T=T_{charge}+T_{discharge}
}$$
これを上で解説した式を代入します。
$$\small{
T=\frac{V_{integ}}{\frac{Vref-V_L}{R_4C_1}}+\frac{-V_{integ}}{\frac{Vref-V_H}{R_4C_1}}
}$$
Vinteg:積分範囲(ヒステリシス幅)[V]
Vref:基準電圧[V]
VL:Low時の出力電圧[V]
VH:High時の出力電圧[V]
T:周期[sec]
f:周波数[Hz]
放電時間も充電時間もR4とC1で決まっているので、同じです。今回の例では0.2msec+0.2msec=0.4msecが1周期です。
周波数はこれの逆数なので、2.5kHzですね。
はい、本記事は以上です。何かの参考になれば幸いです。最後までお読みいただきありがとうございました!!