力率の求め方

今日はPFCコンバータを勉強していて「力率ってどうやって計算するの？」って疑問に思ったので、そのことを記事にします。

力率=有効電力/皮相電力でしょ。いやいやいや、そんなことはわかってる。

PFCコンバータのシミュレーションしたけど、結局この力率ってなんぼなん？

シミュレーションで得られたデータからどうやって有効電力、皮相電力を計算したらいいの？

って話です。

結論_力率の求め方

以下のような交流電源から電力が供給されている回路において、

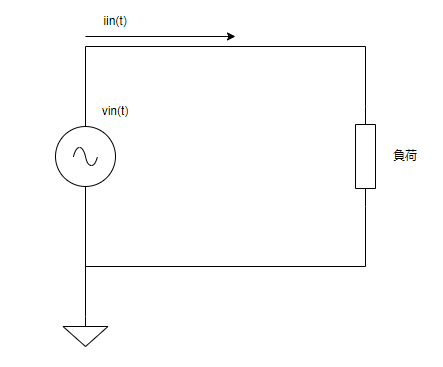
力率は以下の式で表されます。

$$\small{
PF=\frac{\int_0^Tv_{in}(t)i_{in}(t)dt}{\sqrt{\int_0^Tv_{in}^2(t)dt}\sqrt{\int_0^Ti_{in}^2(t)dt}}
}$$

シミュレーションで得られた入力電圧、入力電流をこの式に当てはめて計算してやれば、力率です。

なんでそんな式になるの？

ここのページが分かりやすかったです。

有効電力は実際に使った電力で電力の瞬時値を足していったものの平均で計算できます。つまりv(t)*i(t)を一定時間で積分したものの時間で割った値になります。

$$\small{
有効電力=\frac{1}{T}\int_0^Tv_{in}(t)i_{in}(t)dt
}$$

皮相電力は実効値で計算されます。

$$\small{
皮相電力=V_{rms}*I_{rms}\\
=\sqrt{\frac{1}{T}\int_0^Tv_{in}^2(t)}\sqrt{\frac{1}{T}\int_0^Ti_{in}^2(t)}
}$$

これらの式を力率=有効電力/皮相電力の式に当てはめると1/Tが消えて、

$$\small{
PF=\frac{\int_0^Tv_{in}(t)i_{in}(t)dt}{\sqrt{\int_0^Tv_{in}^2(t)dt}\sqrt{\int_0^Ti_{in}^2(t)dt}}
}$$

この式になります。

確認してみる

式だけ見ても「ふ～ん。。。」って感じなので、実際にシミュレータ(Pspice for TI)で力率を計算してみましょう。

位相差0のパターン

以下の抵抗だけの回路に交流電源を繋げてシミュレーションしてみます。

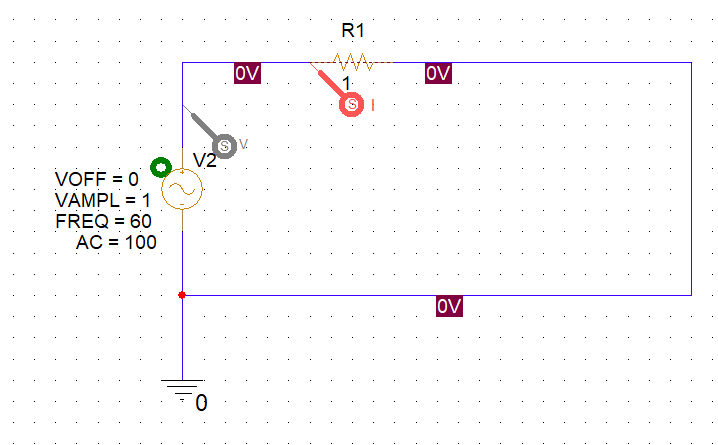
入力電圧と電流波形は以下のように位相差=0。つまり力率=1です。

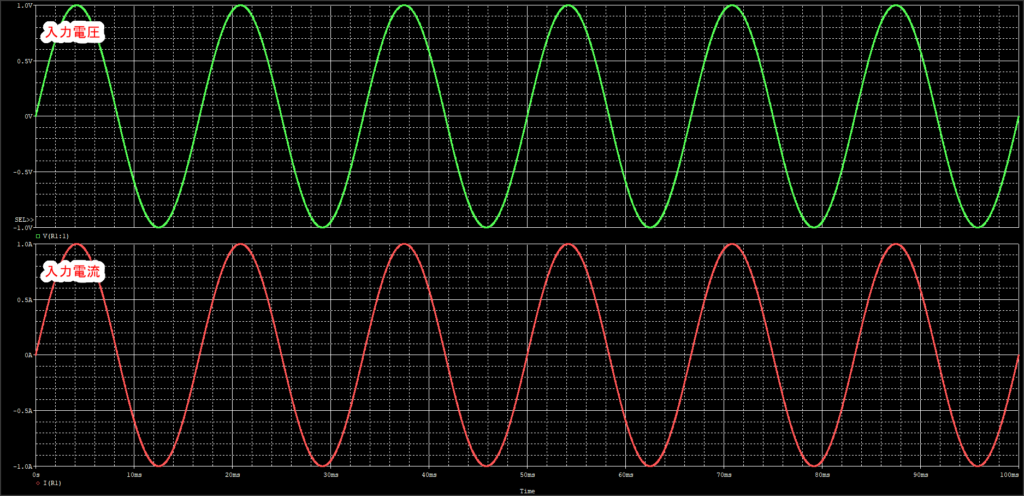
上記の波形に力率を求める式。つまり以下の式を使ってみます。

$$\small{
PF=\frac{\int_0^Tv_{in}(t)i_{in}(t)dt}{\sqrt{\int_0^Tv_{in}^2(t)dt}\sqrt{\int_0^Ti_{in}^2(t)dt}}
}$$

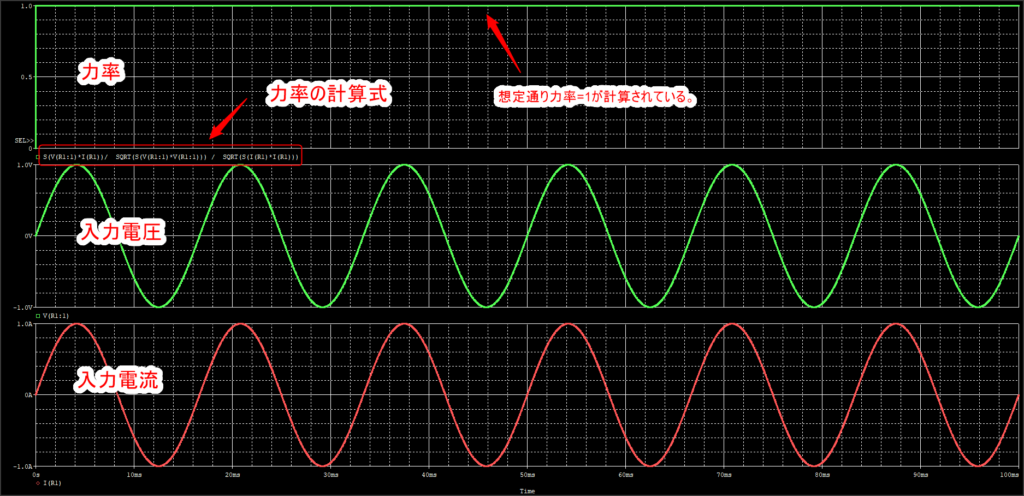
想定通り、力率=1が計算できています。

ちなみに、Pspice for TIでは具体的に以下の手順で計算式を波形に表示できます。

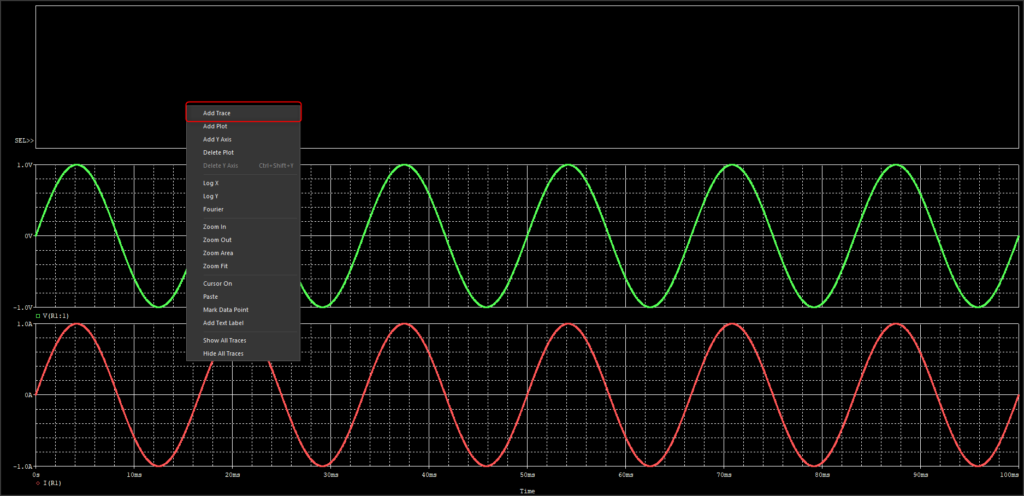
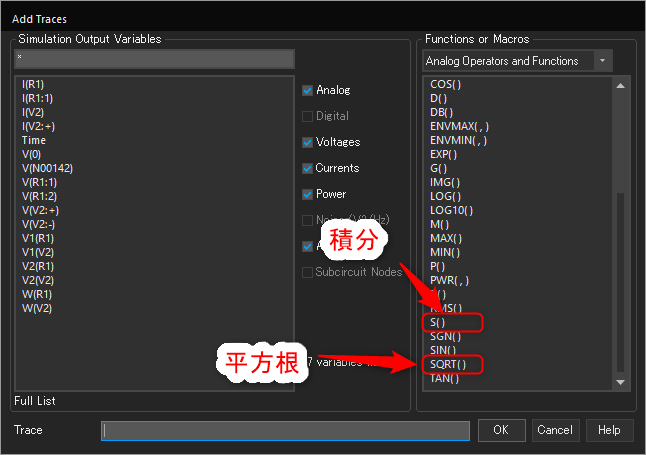
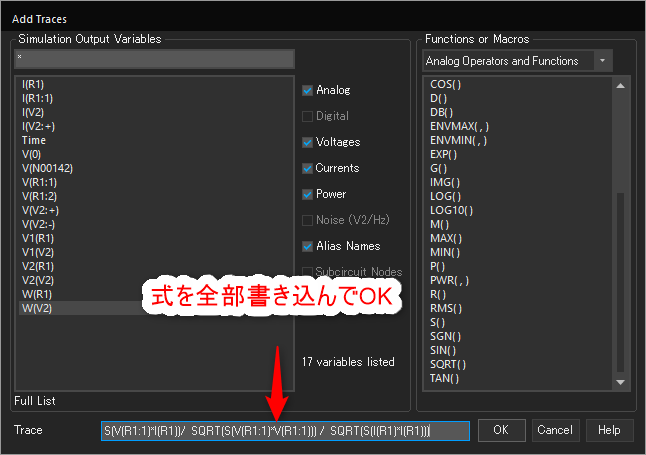
位相差45degくらいのパターン

適当にインダクタを挿入しました。

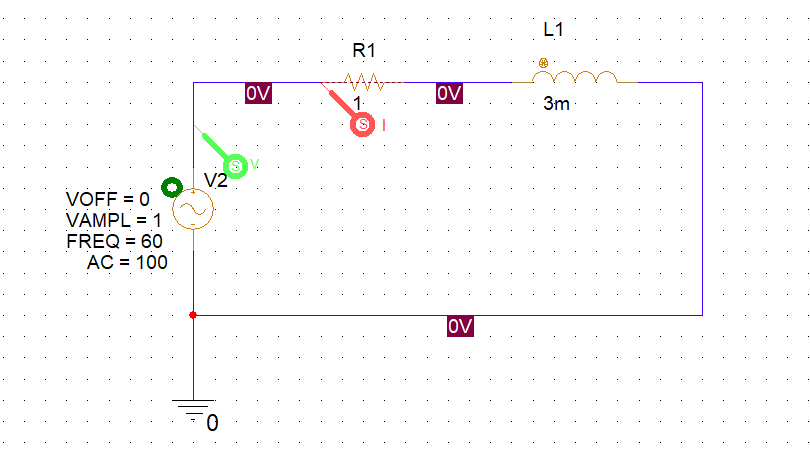
入力電圧と電流波形は以下のように位相差が大体45degになる様に3mHにしました。

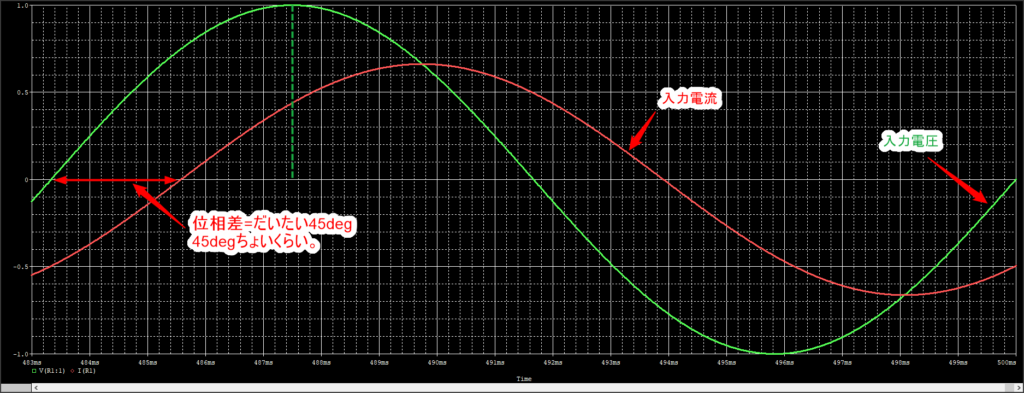
さて、力率を計算すると

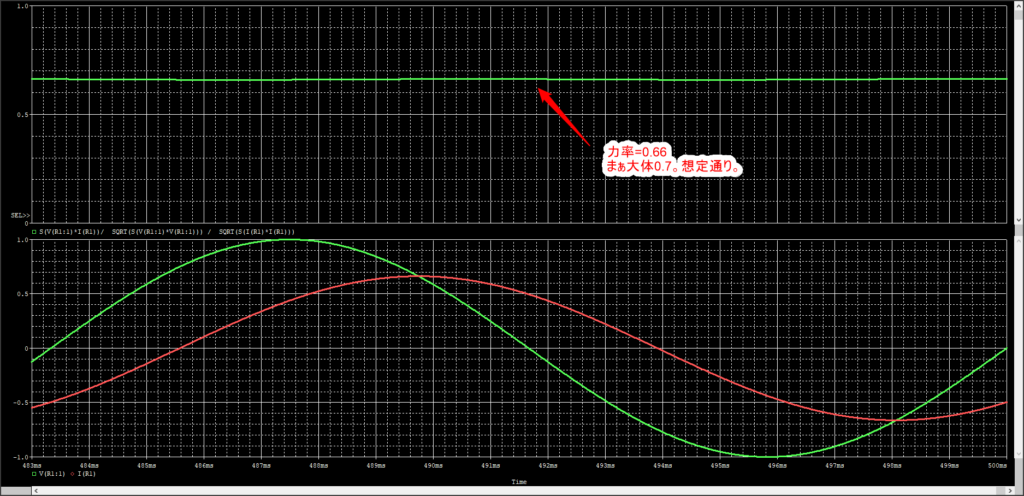
まぁ0.66と大体0.7なので良しとします。

ということで

$$\small{
PF=\frac{\int_0^Tv_{in}(t)i_{in}(t)dt}{\sqrt{\int_0^Tv_{in}^2(t)dt}\sqrt{\int_0^Ti_{in}^2(t)dt}}
}$$

この式を使ってシミュレータでちゃんと力率が計算できていることを確認しました。

はい、以上です。何かの参考になれば幸いです。

最後までお読みいただきありがとうございました！！