みなさま、お疲れ様です。
本日はこの回路↓を取り上げてどう動くのか解説します。良く見る積分回路ですね。
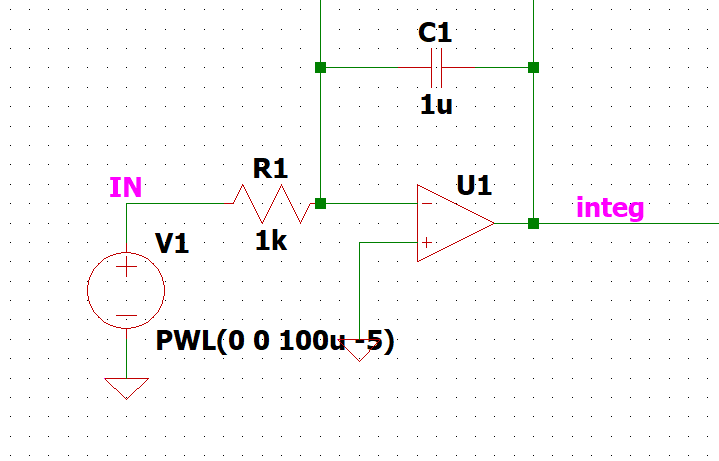
- 積分回路はなぜ積分回路として動くの?
という方の参考になれば幸いです。
では始めます。
どう動くのか?
まず上の回路のシミュレーション結果を示します。
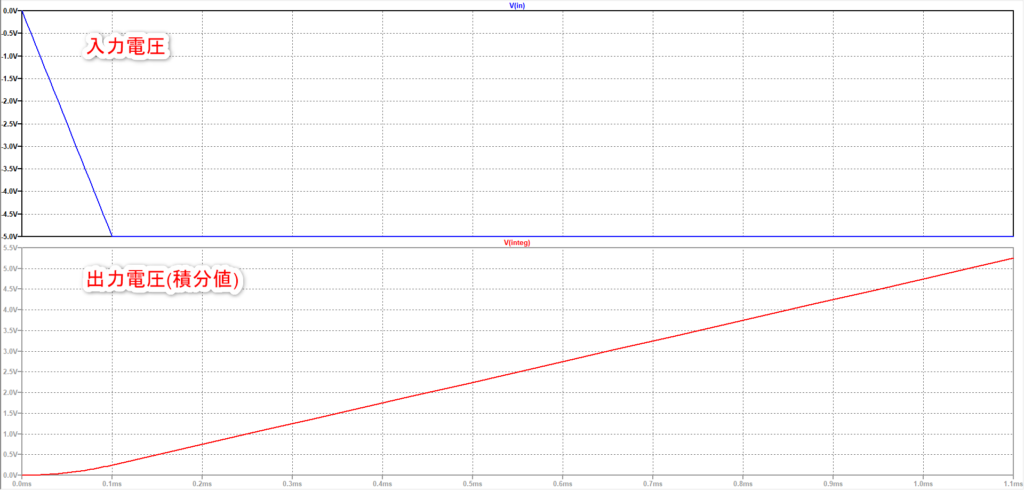
入力電圧に負電圧を入力すると、出力電圧がじわーっと上がっていきます。
これは以下の式で上がっていきます。
$$\small{
V_{integ}=\frac{V_{ref}-V_{in}}{R_1}*\frac{1}{C_1}t
}$$
Vinteg:出力電圧[V]
Vref:基準電圧(オペアンプの正入力)[V]
Vin:入力電圧[V]
t:時間[sec]
今回の例ではVref=0V、Vin=-5V、R1=1kΩ、C1=1μFで出力電圧は
$$\small{
V_{integ}=\frac{0-(-5)}{1k}*\frac{1}{1u}t=5[V/msec]
}$$
5V/msecで上昇していきます。ではなぜこうなるのか?を解説します。
なぜそう動くのか?
まず各ノードの電圧を書いていきます。
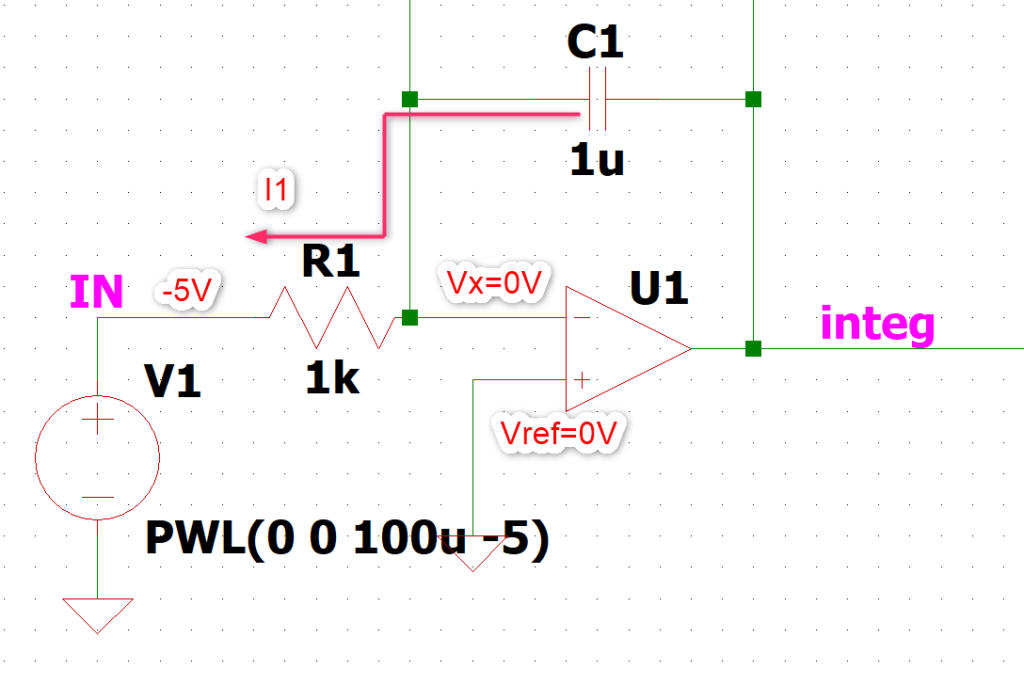
Vx電圧はイマジナリーショートなので+電圧と同じ0Vとなります。
R1に流れる電流はオームの法則で以下の計算式で計算できます。
$$\small{
I_1=\frac{V_{ref}-V_{in}}{R_1}
}$$
この電流が流れる経路はC1しか流れません。出力からC1に向かって充電されます。充電され電圧が上昇されていきます。電圧上昇はQ=CVを思い出しましょう。
Q=CVについてはこちら記事で解説しております。よかったら読んでみて下さい。
$$\small{
V_{integ}=\frac{I_1}{C}t\\
V_{integ}=\frac{\frac{V_{ref}-V_{in}}{R_1}}{C}t\\
V_{integ}=\frac{V_{ref}-V_{in}}{R_1}*\frac{1}{C_1}t
}$$
イマジナリーショートを利用して定電流を作って、コンデンサに充電して、出力電圧をじわーっと上げるってイメージですね。
はい、以上です。
誰かの参考になれば幸いです。最後までお読みいただきありがとうございました!!

