お疲れ様です。
本記事はパワエレ回路の重要部品であるリアクトルについて
インダクタンス値をどれだけ変化すると体積はどれだけ変わるのか?
ということについて検討した記事です。
「スイッチング周波数を速くするとインダクタンス値は下げれる。そしたら小型化になる。」この一般論に対して、どのくらい小型化になるのか?を具体的な数値で示したい方の参考になれば幸いです。
【結論】リアクトルの体積比を求める式
まず結論です。L1とL2のインダクタンス値が異なるリアクトルがあったときその体積比は以下の式で計算することが出来ます。
$$\small{
\frac{体積_1[m^3]}{体積_2[m^3]}
=\left( \frac{ L_1 \left( I_{ave} +\frac{1}{2}ΔI_{L1} \right)^2}{ L_2 \left( I_{ave} +\frac{1}{2}ΔI_{L2} \right)^2} \right) ^{\frac{3}{4}}
}$$
L:インダクタンス値[H]、Iave:平均電流[A]、ΔIL:リップル電流[A]
「リアクトルと電流ピーク値の2乗を掛けた値の比を取って、3/4乗したら出るよ。」って式ですね。
式を見るとインダクタンス値を下げれば下げる程、リップル電流が大きくなりピーク値が大きくなるから、「インダクタンス値を下げて体積が小さくなる。」という一般論はまぁ正しいけど、限界ありそうだよね。って感じる式です。
ちなみにこの式はエリアプロダクト法から私が計算しただけの値なので、正しいかは保証はしませんが、たぶん合ってると思います。(なんじゃそりゃ)
導出過程を解説していこうと思いますので、納得したら使ってみて下さい。
エリアプロダクト法と体積見積もりの計算式
エリアプロダクト法とは?
エリアプロダクト法とはリアクトルやトランスのコアの選定方法です。
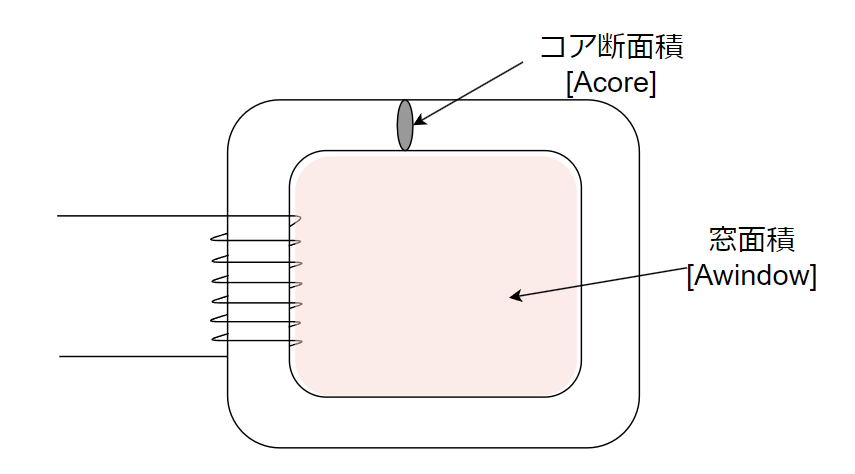
コアの断面積Acore[m^2]とコアの窓面積Awindow[m^2]の掛け算をAp値とします。
$$\small{
A_p[m^4]=A_{core}[m^2]×A_{window}[m^2]
}$$
窓面積とコア断面積を色々計算していくと、Ap値の計算式は以下となります。
$$\small{
A_p[m^4] = \frac{L I_{Lmax}^2}{K_w J_{max} B_{max}}
}$$
ILmax:リアクトルに最大電流値[A]、Kw:占積率(=窓面積に占める巻き線の面積)、Jmax:電流密度[A/m^2]、Bmax:最大磁束密度[T]
このAp値より大きいAp値のコアを選択したら良いよ。というのがエリアプロダクト法によるコアの選定方法になります。
体積を見積もる式
このAp値がm^4なので、これを3/4乗して、コア形状ごとの係数Kvolをかけると体積になります。
$$\small{
体積[m^3] =Kvol ( A_p[m^4] ) ^{\frac{3}{4}} \\
= Kvol\left( \frac{L I_{Lmax}^2}{K_w J_{max} B_{max}} \right)^{\frac{3}{4}}
}$$
Kvol:コア形状ごとの係数
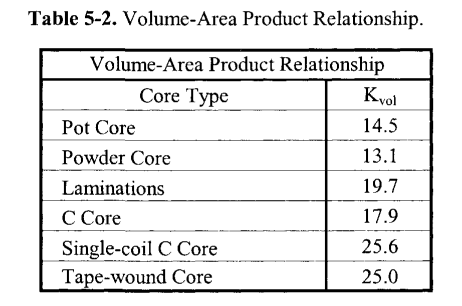
このKvolというのはこちらの参考資料によれば、以下の値を使用したら良いようです。
2つのリアクトルの体積比を計算する式の導出過程
さて先ほどの体積の式で2つのリアクトルの体積を計算して、比較したらいいんですが、それにはKvol、Kw、Jmax、Bmaxを決めてやらねばなりません。
それを考えるのはめんどくさいです。ってかこの式を割り算してやれば体積比は出てくるし、定数は消えて単純な式が出てきそうですよね。
それをやってみたら、最初の式が出てきます。
実際に計算してみます。
まずインダクタンス値L1のリアクトルの体積は
$$\small{
体積_1[m^3] =K_{vol}\left( \frac{L_1 I_{L1max}^2}{K_w J_{max} B_{max}} \right)^{\frac{3}{4}}
}$$
そしてインダクタンス値L2のリアクトル体積は
$$\small{
体積_2[m^3] =K_{vol}\left( \frac{L_2 I_{L2max}^2}{K_w J_{max} B_{max}} \right)^{\frac{3}{4}}
}$$
いま、このリアクトル体積の比を求めようとしているから、単純に割る。Kvolは消えます。
$$\small{
\frac{体積_1[m^3]}{体積_2[m^3]}
=\frac{\left( \frac{L_1 I_{L1max}^2}{K_w J_{max} B_{max}} \right)^{\frac{3}{4}}}{\left( \frac{L_2 I_{L2max}^2}{K_w J_{max} B_{max}} \right)^{\frac{3}{4}}}
}$$
乗は括る。
$$\small{
\frac{体積_1[m^3]}{体積_2[m^3]}
=\left(\frac{ \frac{L_1 I_{L1max}^2}{K_w J_{max} B_{max}}}{\frac{L_2 I_{L2max}^2}{K_w J_{max} B_{max}}}\right) ^{\frac{3}{4}}
}$$
分母同じだから消す。これで定数は消え去りました。
$$\small{
\frac{体積_1[m^3]}{体積_2[m^3]}
=\left( \frac{ L_1 I_{L1max}^2}{L_2 I_{L2max}^2} \right) ^{\frac{3}{4}}
}$$
ILmaxは平均値+1/2ΔILだから
$$\small{
\frac{体積_1[m^3]}{体積_2[m^3]}
=\left( \frac{ L_1 \left( I_{ave} +\frac{1}{2}ΔI_{L1} \right)^2}{ L_2 \left( I_{ave} +\frac{1}{2}ΔI_{L2} \right)^2} \right) ^{\frac{3}{4}}
}$$
はい、これで最初の式が出てきましたね。これだと回路を検討している段階でリアクトルの体積を比べられるって感じですね。
試しに計算してみよう!
例えば、インバータにおいてインダクタンス値を2mHから1mHに変更したときを考えてみます。
計算する仕様は以下に適当に設定しました。
| VDC | 400V |
| fsw | 20kHz |
| Iave_rms | 5A |
インバータのリップル電流は以下の式で計算できます。
$$\small{
ΔI_L=\frac{V_{DC}}{4Lf_{sw}}
}$$
VDC:DC電圧[V]、fsw:スイッチング周波数[Hz]
ちなみにこの式がなぜこの式になるのかはこちらの記事で解説してます。良かったら見てみて下さい。
さて、実際に体積比を計算してみると、、、
$$\small{
\frac{体積_1[m^3]}{体積_2[m^3]}
=\left( \frac{ 1m \left( 5 +\frac{1}{2}*\frac{400}{4*1m*20k} \right)^2}{ 2m \left( 5 +\frac{1}{2}*\frac{400}{4*2m*20k} \right)^2} \right) ^{\frac{3}{4}}
}$$
$$\small{
\frac{体積_1[m^3]}{体積_2[m^3]}
=\left( \frac{ 1m \left( 7.5 \right)^2}{ 1m \left( 6.25 \right)^2} \right) ^{\frac{3}{4}}
}$$
$$\small{
\frac{体積_1[m^3]}{体積_2[m^3]}
=\left( \frac{ 0.05625 }{ 0.078125 } \right) ^{\frac{3}{4}}
}$$
$$\small{
\frac{体積_1[m^3]}{体積_2[m^3]}≒0.78
}$$
つまり、2mHから1mHに変わると、体積がおおよそ22%減少するよ。ということになりますね。
より厳密に比較する場合は「Ap値を計算してコアを選択して比較する。」とより良いかもしれません。しかし、これでも参考値にはなるのではないでしょうか。
はい、以上で本記事は終わります。
誰かの参考になれば幸いです。最後までお読みいただきありがとうございました!!!
参考資料
高 パ ワ ー 密 度 を 実 現 す る マ ル チ レ ベ ル変 換 器 ト ポ ロ ジ ー の 多 角 的 評 価 法(pdf 50ページ、式2-20)