皆様、お疲れ様です。こないだとある半導体製品の故障率を計算する機会がありました。そのときに「( ,,`・ω・´)ンンン??」となったので、その内容を備忘録的に記事に致します。
具体的には以下の故障率を計算する2つの式です。
①$$故障率=\frac{FIT}{10^9}×(t×m)$$
②$$故障率=1-exp((-\frac{t}{η})^β)$$
FIT:fit率
t:稼働時間
m:サンプル数
η:特性寿命パラメータ
β:形状パラメータ
①はFIT率が10億サンプル×時間だから10億で割って、じゃあ実際の総サンプル×総時間分だとどのくらいになるのか?を直している式ですね。なんか納得感のある式です。
②はワイブル分布によってモデル化された式のようです。exp(-〇〇t)って式なので、確率的にはこんな感じになりますね↓。
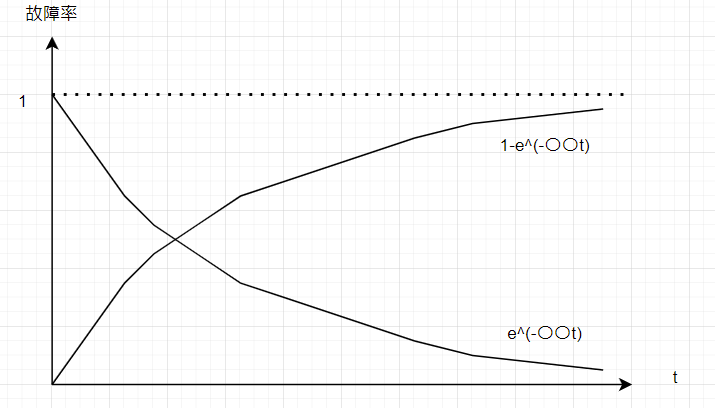
なるほどねぇと。これはこれで最初が故障が起きやすくて、じわーっと故障率が安定していく様子が表現されているなぁ。とこちらもまぁ納得できる式です。
この二つの式の違いは何なのか?
私と同じように疑問に思っている方の参考になれば幸いです。
【結論】バスタブカーブの領域によって使い分ける
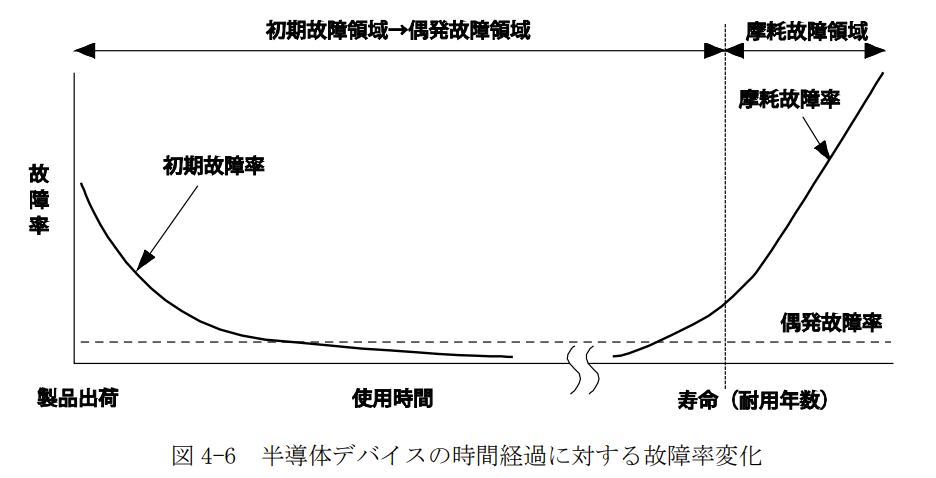
半導体に関わったことある人であればバスタブカーブはご存じだと思います。製品出荷後に故障率が多くて、次第に安定的になる。長い時間を経て製品寿命を迎えて故障率が増えていく。
上図における初期故障を表現しているのが②の式
例えば、とあるICを100万個出荷する。稼働時間は大体10000時間です。信頼性試験の結果FIT率は1FITです。じゃあ市場でどんだけ故障する可能性があるかを見積もりたい。と思ったとしたら②の式を使えば良いよってことですね。たぶんはい。
いや、厳密に合計を計算したいのであれば、市場で発生する初期故障率も考慮しないといけませんね。であれば、
市場におけるライフサイクル故障率=①+②
となると考えられます。うーん。まだ理解が浅いですね。まだまだ使いこなすには修練が必要です。
うーん。信頼性って難しい。
参考資料
ソニー信頼性ハンドブック:https://www.sony-semicon.co.jp/csr/common/pdf/Handbook_j_202004.pdf
ルネサス信頼性ハンドブック:https://www.renesas.com/jp/ja/document/oth/semiconductor-reliability-handbook?language=ja
TI信頼性関連用語:https://www.tij.co.jp/ja-jp/support-quality/reliability/reliability-terminology.html