2段オペアンプ↓の設計方法を解説してみようという試みの記事の3回目です。
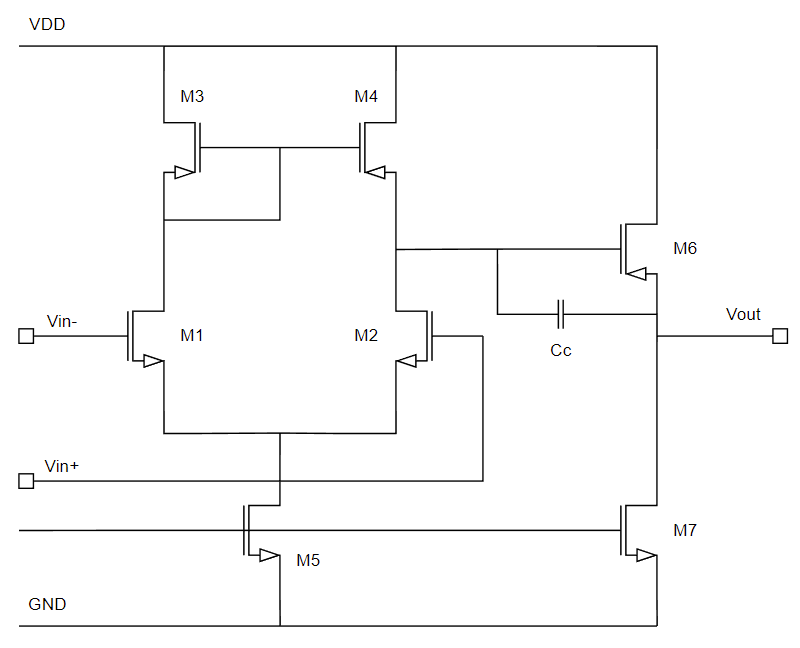
前回記事では2段オペアンプの伝達関数からゲインや折れ点周波数を計算しました。
本記事では、谷口先生本に出てくる条件式(gm6=10gm1、Cc>0.2Cout)はなんでそうなるのか?を解説してみようと思います。
1回目:【2段オペアンプ設計方法】小信号等価回路化してDCゲインを計算してみる
2回目:【2段オペアンプの設計方法】周波数特性の計算をしてみる
3回目:【2段オペアンプの設計方法】なぜ設計条件(gm6=10gm1、Cc>0.2Cout)なのか?(本記事)
・谷口先生本のP189 「gm6=10gm1、Cc>0.2Cout」で挫折しました。
・なーにが「これがミラー補償法に基づくOPアンプを設計する際の制約条件なのです。」だ!さっぱりわからんぞ!!!!!おーーーーい!!!!!
という超ピンポイントの悩みをお持ちの方へ解決となれば、非常に嬉しいです。
では、始めます。
前回のおさらい
前回記事では伝達関数から以下の特性を求めました。
DCゲイン:$$Av=R1R2gm2gm6$$
ゼロ点周波数:$$z=\frac{gm6}{Cc}$$
ポール周波数①:$$p1=\frac{-1}{gm6R1R2Cc}$$
ポール周波数②:$$p2=\frac{-gm6}{C2}$$
ボード線図に描くと以下のような感じです。
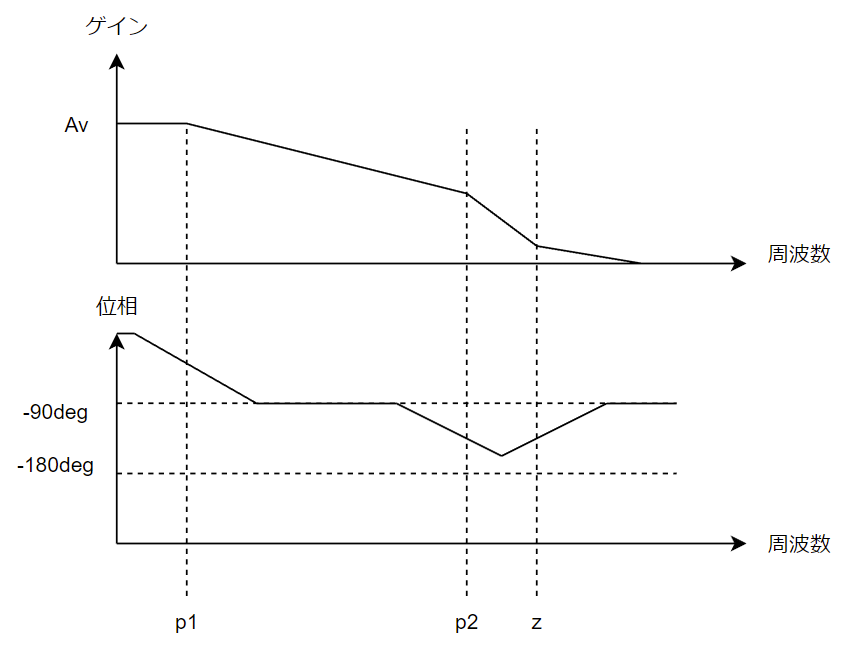
こっから、設計条件を導くのに「オペアンプの安定性を確保するにはどうしたら良いか?」を考えます。
ナイキストの安定判別法の安定条件から計算する
ナイキストの安定判別法を使えば一巡伝達関数のボード線図から安定性を判別することが出来ます。
ボード線図から安定性を判別する方法については以下の記事で詳しく解説しておりますので、良かったら読んでみて下さい。
↑こちらの記事では安定性の目安は位相余裕度≧45deg、ゲイン余裕度≧6dBと解説しました。↓の図の青線が位相余裕度、赤線がゲイン余裕度です。
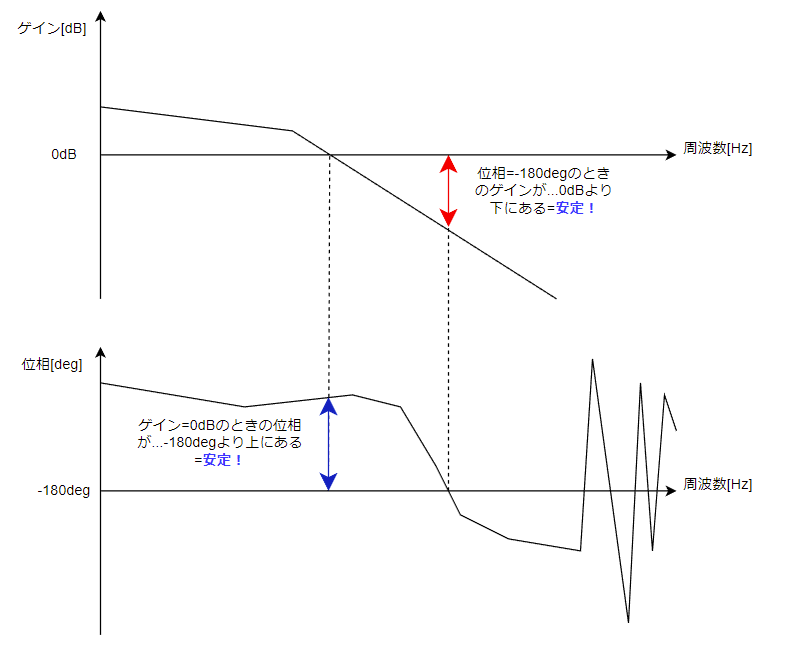
今回はより保守的に位相余裕度>60deg以上を一つの目安とします。つまり
$$(2段オペアンプの位相余裕度を計算する式)>60deg$$
が設計条件になるわけです。
さて、粗めの設計条件が出てきたので次は2段オペアンプの位相余裕度はどうやって計算すればいいのか?を考えます。
2段オペアンプの位相余裕度はどうやって計算するのか?
まずは伝達関数から偏角を求める式を思い出すか、調べるかしましょう。(制御工学の教科書の最初の方に書いてあるはずです。)
偏角を求める式は以下になります。
$$tan^{-1}(\frac{Im}{Re})$$
アークタンジェントが出てきてしまいました。辛いですね。
ちなみに角周波数ωにおける、各ポール、ゼロによる偏角は以下の式で計算することが出来ます。
$$偏角_{p1}=tan^{-1}(\frac{ω}{p1})、偏角_{p2}=tan^{-1}(\frac{ω}{p2})、偏角_{z}=tan^{-1}(\frac{ω}{z})$$
なぜかというと、例えば、以下のようなポールpを持つ伝達関数があったとします。
$$G_p=\frac{a}{s-p}$$
aは適当な定数です。この式を実部と虚部に分けようとしたら、s=jωに直して
$$G_p=\frac{a}{jω-p}$$
分子分母にjω+pを掛けて
$$G_p=\frac{a(jω+p)}{-ω^2+p^2}$$
jが付くのが虚部という感じですね。
$$G_p=\frac{aωj}{-ω^2+p^2}+\frac{ap}{-ω^2+p^2}$$
これの偏角なので
$$偏角_{Gp}=tan^{-1}(\frac{\frac{aω}{-ω^2+p^2}}{\frac{ap}{-ω^2+p^2}})$$
いい感じに分子分母を約分して
$$偏角_{Gp}=tan^{-1}(\frac{ω}{p})$$
だけが残ります。これを各ポール、ゼロで同じようにしていると、こうなります↓。
$$偏角_{p1}=tan^{-1}(\frac{ω}{|p1|})、偏角_{p2}=tan^{-1}(\frac{ω}{|p2|})、偏角_{z}=tan^{-1}(\frac{ω}{z})$$
そして、位相余裕度は-180degまであとどのくらいあるか?なので、
$$位相余裕度=180deg-(tan^{-1}(\frac{ω_u}{|p1|})+tan^{-1}(\frac{ω_u}{|p2|})+tan^{-1}(\frac{ω_u}{z}))$$
となります。
ωuは「ゲインが0dBになるときの周波数」です。よくユニティゲイン周波数って言われたりしますので、ωuとしています。
これで2段オペアンプの位相余裕度を計算する式が出ました。これが60deg以上あればいいのです。つまり
$$180deg-(tan^{-1}(\frac{ω_u}{|p1|})+tan^{-1}(\frac{ω_u}{|p2|})+tan^{-1}(\frac{ω_u}{z}))>60deg$$
となります。おぼろげにゴールが見えてきた感じでしょうか。
ユニティゲイン周波数はいくつになるのか?
あとはユニティゲイン周波数が分かれば、↑の計算式に代入して行けそうな雰囲気が出ています。
で、ユニティゲイン周波数はp1から求めることが出来ます。
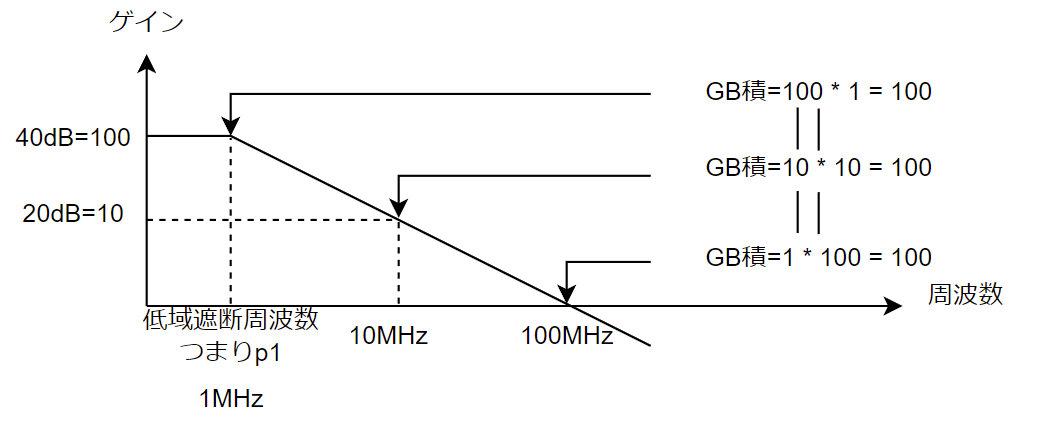
GB積って知ってますかね?オペアンプの性能の一つです。
wikiから引用すると
GB積(ジービーせき、Gain Band width product、利得帯域幅積)とは、増幅器の特性をあらわす指標のひとつ。増幅器の開ループ利得Aと、利得が半減 (3 dB 減衰) する周波数fcの積であり、単位にはヘルツ [Hz] を用いる
https://ja.wikipedia.org/wiki/GB%E7%A9%8D
たとえば、利得が10倍で低域遮断周波数が2 MHzのオペアンプならば
GBW=A*fc=10*2MHz=20MHz
となる。
GB積の大きなオペアンプは、より高い周波数帯域まで安定して増幅することができる。
絵で表すとこんな感じです↓。(書きやすく、Av=40dB(=100)、fc(p1周波数)=1MHzとしました。)
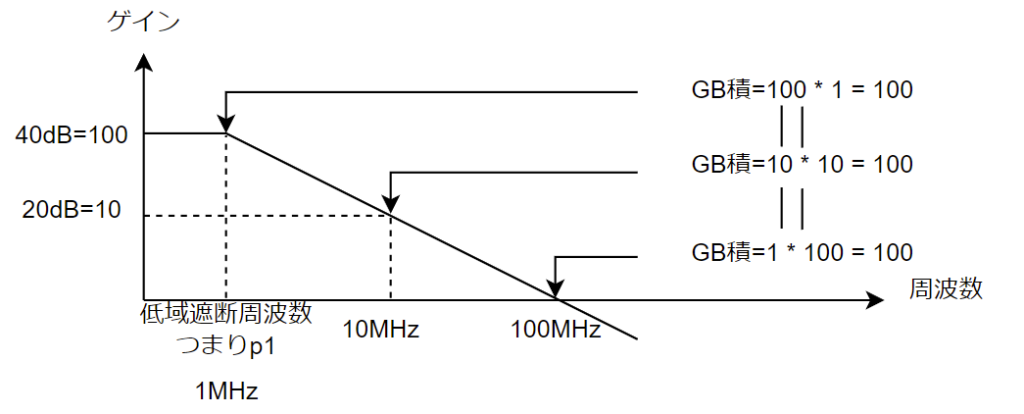
「0dBまではどこの周波数で見てもGB積は一定。」っていうのは
つまり「p1周波数から0dBまで一定(-20dB/dec)で落ちて行っている。」ということです。
それが成り立つのはつまり「p2とzの周波数が0dBより高周波数にある。」ってことです。
オペアンプはなんでGB積が一定になるかわかりますかね?単純でそうなるように設計するからです。
だから、つまりですね。オペアンプはp2とzの周波数は0dBよりも高いところに置くように設計するって言うのが前提なんです。
そう考えると0dB(ゲイン=1)に交差する周波数(ユニティゲイン周波数)は「GB積は一定だよ。」って考え方とp1周波数とDCゲインAvから計算できます。
$$ω_u*1=Av*|p1|$$
ポール周波数①:$$p1=\frac{-1}{gm6R1R2Cc}$$
DCゲイン:$$Av=R1R2gm2gm6$$
なので
$$ω_u=R1R2gm2gm6*\frac{1}{gm6R1R2Cc}$$
$$ω_u=\frac{gm2}{Cc}$$
さて、ユニティゲイン周波数ωuが求まりました。
位相余裕度の式にωuを代入してp1の偏角を消す
$$180deg-(tan^{-1}(\frac{ω_u}{|p1|})+tan^{-1}(\frac{ω_u}{|p2|})+tan^{-1}(\frac{ω_u}{z}))>60deg$$
まずはp1に代入しましょう。
$$180deg-(tan^{-1}(\frac{\frac{gm2}{Cc}}{\frac{1}{gm6R1R2Cc}})+tan^{-1}(\frac{ω_u}{|p2|})+tan^{-1}(\frac{ω_u}{z}))>60deg$$
$$180deg-(tan^{-1}(gm2gm6R1R2)+tan^{-1}(\frac{ω_u}{|p2|})+tan^{-1}(\frac{ω_u}{z}))>60deg$$
と中身がDCゲインになりました。
$$180deg-(tan^{-1}(Av)+tan^{-1}(\frac{ω_u}{|p2|})+tan^{-1}(\frac{ω_u}{z}))>60deg$$
アークタンジェントをこんなん↓ですね。
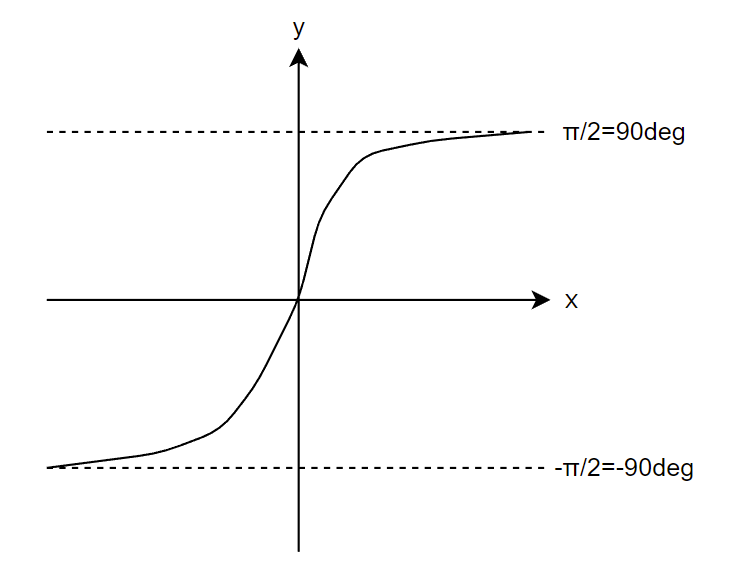
Avはくっそデカい定数なので、tan-1(∞)です。つまりy=90degですね。それを踏まえて、、、
$$180deg-90deg-tan^{-1}(\frac{ω_u}{|p2|})-tan^{-1}(\frac{ω_u}{z}))>60deg$$
$$90deg-tan^{-1}(\frac{ω_u}{|p2|})-tan^{-1}(\frac{ω_u}{z}))>60deg$$
ふぅ。一歩前進しましたね。
次は位相余裕度の式にωuを代入してzの偏角を消す
さて、一個ずつ撃破していきましょう。zの偏角にユニティゲイン周波数ωuを代入します。
$$tan^{-1}(\frac{ω_u}{z})$$
$$tan^{-1}(\frac{\frac{gm2}{Cc}}{\frac{gm6}{Cc}})$$
$$tan^{-1}(\frac{gm2}{gm6})$$
ここでゼロ点周波数をユニティゲイン周波数ωuより10倍よりでかい位置に置くとします。
(まぁゼロ点周波数はユニティゲイン周波数ωuより大きい位置に置くのはGB積の前提から明らかなので、まぁ10倍なのもまぁ多少はね。)ということで。
$$z>10ω_u$$
代入して解くと
$$gm6>10gm2$$
ワーストで偏角が回るのがgm6=10gm2のときです。
ここで唐突に1つ目の条件が出てきました。まぁその値を偏角計算式に代入してみます。
$$tan^{-1}(0.1)=5.7deg$$
なので、ユニティゲイン周波数ωuにおけるゼロ点周波数の偏角は5.7deg回ってます。なので
$$90deg-tan^{-1}(\frac{ω_u}{|p2|})-5.7deg>60deg$$
$$90deg-60deg-5.7deg>tan^{-1}(\frac{ω_u}{|p2|})$$
$$tan^{-1}(\frac{ω_u}{|p2|})<24.3deg$$
あとちょっとあとちょっと!!!!!!
|p2|=の式に直す!
$$tan^{-1}(\frac{ω_u}{|p2|})<24.3deg$$この式を|p2|=の式に直していきます。
$$y=tan(x)$$のとき$$x=tan^{-1}(y)$$なので
$$tan(24.3deg)>\frac{ω_u}{|p2|}$$
解きます。
$$|p2|>\frac{ω_u}{tan(24.3deg)}$$
1/tan(24.3deg)=2.2です。
$$|p2|>2.2ω_u$$
つまり
$$\frac{gm6}{C2}>2.2\frac{gm2}{Cc}$$
gm6=10gm2なので
$$\frac{10gm2}{C2}>2.2\frac{gm2}{Cc}$$
$$\frac{1}{C2}>0.22\frac{1}{Cc}$$
$$Cc>0.22C2$$
あーでてきました。疲れましたね。
つまりgm6=10gm2としておいて、位相補償コンデンサCc>0.22C2にしておけば、位相余裕度を60deg以上を確保できますよってことが導かれましたね。
本記事は以上です。誰かの参考になれば幸いです。
本当にここまで読んで頂いてありがとうございました!!!