みなさま、お疲れ様です。
理想的なコンデンサは、以下の式に応じてインピーダンスが周波数に応じて単純に小さくなります。
$$\small{
Z=\frac{1}{j\omega C}
}$$
しかし、現実のコンデンサはそれほど単純ではありません。
実際には、ESR(等価直列抵抗)やESL(等価直列インダクタンス)が存在し、高周波になるにつれてインピーダンスが再び上昇する傾向があります。
本記事では、一般的なコンデンサのデータシートからモデルを構築する方法と、そのモデルを用いた周波数特性の確認手法を解説します。
コンデンサの等価回路モデル
現実のコンデンサは以下のような回路で近似できます。
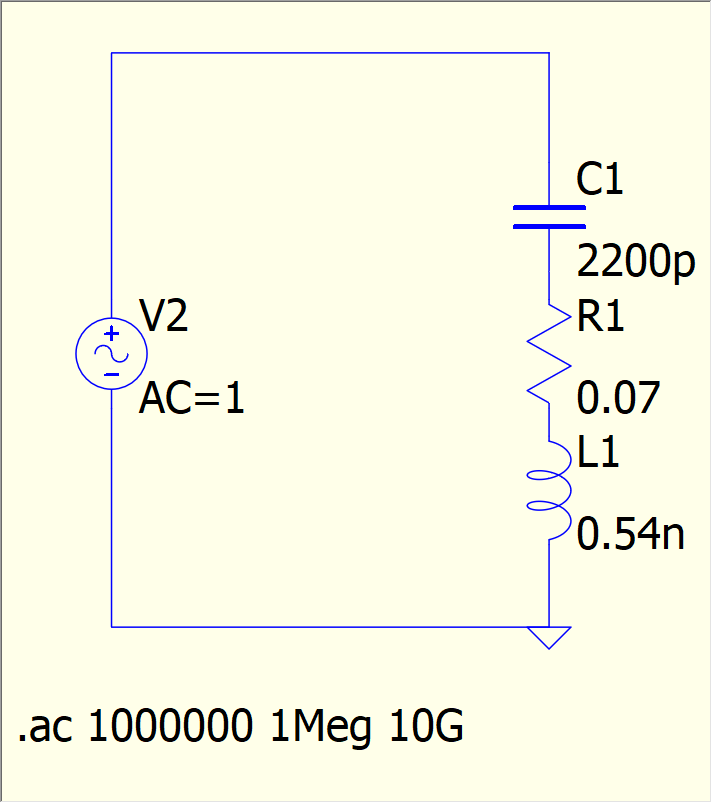
CとRとLを直列接続した回路で表現できます。
では、次にどうやってC,R,Lの値を決めたら良いかを説明します。
モデル化手順(3ステップ)
以下の3ステップで、実コンデンサの周波数特性をモデル化することができます。
ステップ1:容量値(C)を決める
まずは基本となる静電容量を決めます。
これは使用するコンデンサーの公称容量値(例:10μFなど)をそのまま使用します。
ステップ2:ESRを読み取る
データシートに記載された「インピーダンス vs 周波数」グラフから、
インピーダンスが最も低くなる周波数(谷底)の値を確認します。
このときのインピーダンスがESR(等価直列抵抗)に相当します。
なぜこれがESR?
- この点は、容量成分 ( C ) と寄生インダクタンス ( L ) の共振周波数に相当します。
- 共振周波数では ( C ) と ( L ) のリアクタンスが打ち消し合うため、抵抗成分だけが残るのです。
ステップ3:ESLを逆算する
先ほどの谷底の周波数、共振周波数をデータシートから読み取り、次式に代入してESL(L)を計算します。
$$\small{
L= \frac{1}{ (2\pi fc)^2*C }
}$$
等価回路の構成と確認方法
上記の3つのパラメータ(C, ESR, ESL)を直列接続すれば、
周波数特性を再現するための等価回路モデルが完成します。
このモデルを使って、SPICEなどの回路シミュレータでACスイープ解析を行うことで、
現実のコンデンサーの挙動に近い特性を確認できます。
シミュレーションで確認した結果
では、試しにこちらのコンデンサを例にモデル化してみましょう。インピーダンス特性は以下の通りです。
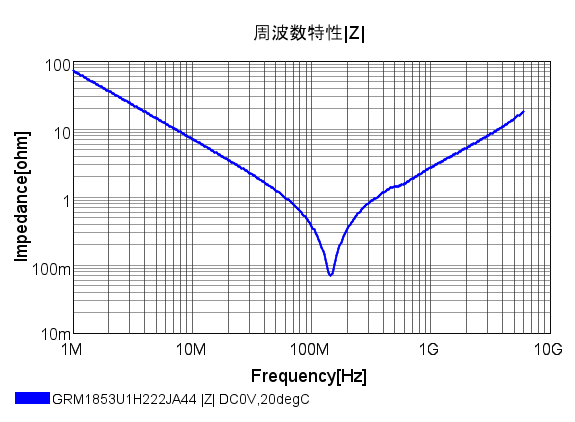
まずこのコンデンサの公称容量は2200pFです。したがって、C=2200pFです。これでSTEP1終わり。
次にこの周波数特性の谷を見ます。0.07Ωになっています。したがって、R=0.07です。これでSTEP2終わり。
最後に谷の周波数を見ます。だいたい146MHzです。以下の式に当てはめて、L値を計算します。
$$\small{
L=\frac{1}{(2\pi146M)^2*2200p}=0.54n
}$$
これでL=0.54nHと決まりました。
回路図にして、シミュレーションしてみます。今回はQspiceを使いました。

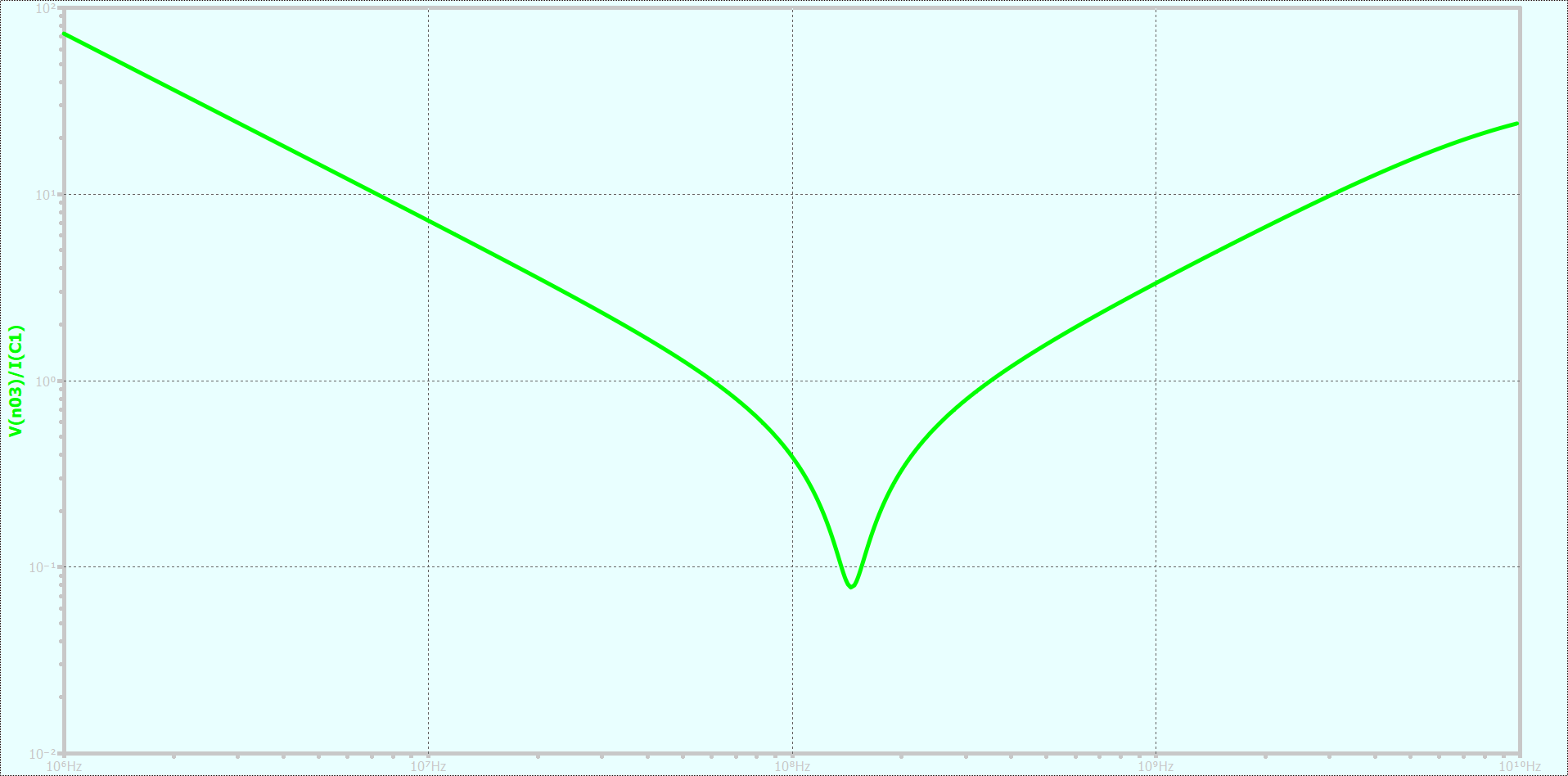
シミュレーション結果が以下の通りです。
デフォルトだとdBでプロットされるので、縦軸を右クリックして、dBからLOGに変更すると上図のようになります。

改めて見比べてみると、一致してますね。
まとめ
- 理想的なコンデンサーと違い、現実のコンデンサーにはESRやESLといった非理想成分が存在します。
- データシートのインピーダンス特性から、簡易モデル(RLC直列回路)を作成することが可能です。
- このモデルを使えば、高周波でのノイズ特性やデカップリング性能なども、事前に評価できます。