みなさま、お疲れ様です。
今回はフィルタ設計に関するちょっとした話です。
みなさん
ある周波数で〇dB落とすには、フィルタのカットオフ周波数は何Hzずらせばいいんだ?
と思ったことはないでしょうか?
例えば図にすると以下のイメージです↓。
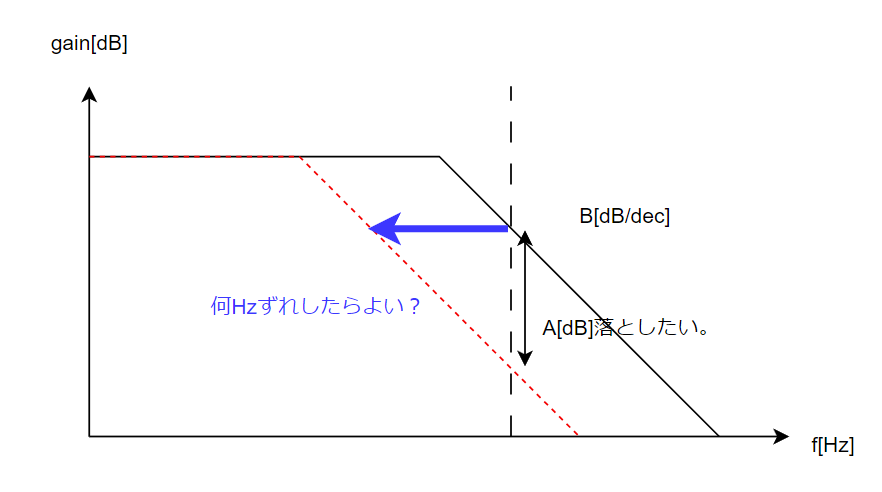
この周波数をどう計算したら良いのか?という話について解説します。
【結論】こう計算しろ!
さっそく結論です。
カットオフ周波数fc[Hz]でA dB/decで落ちていくローパスフィルタでB dB落としたいときは狙いのカットオフ周波数fc_狙い[Hz]は以下の計算式で計算できます。
$$\small{
f_{c狙い}=10 ^{log_{10}(f_c) – \frac{B}{A}}
}$$
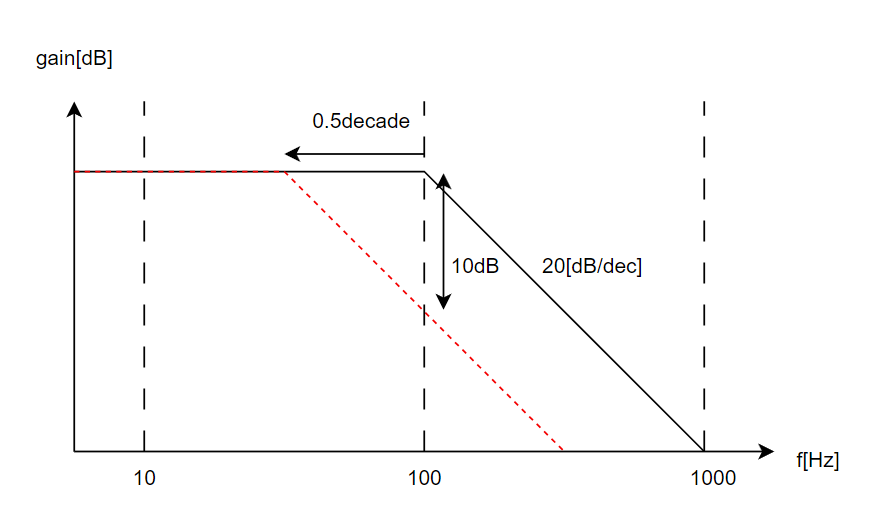
例えばfc=1kHzの-20dB/decで落ちるローパスフィルタで10dB落としたいときは
$$\small{
f_{c狙い}=10 ^{log_{10}(1000) – \frac{10}{20}}\\
f_{c狙い}=10^{3-0.5}=10^{2.5}=316.2[Hz]
}$$
つまり、カットオフ周波数を316.22Hzにしたら、今より10dBほど落とすことが出来ます。
なぜそうなるのか?
一個ずつ考えたら簡単です。
$$\small{
\frac{B}{A}
}$$
これは何decade小さくしたら良いか?を計算してます。先ほどの例だと-20dB/decの傾きに対して10dBずらしたいので、10/20=0.5decadeずらせば良いということです。
$$\small{
log_{10}(f_c)
}$$
この式はカットオフ周波数をdecadeに直しているだけです。先ほどの例だとlog10(1000)=3となります。
つまりdecade単位だと”3から0.5を下げれば良い。”ということなので、狙い値は以下の式になります↓。
$$\small{
log_{10}(f_c)-\frac{B}{A}
}$$
そしてこの数値はdecadeなので、周波数に変換します。
$$\small{
10^{log_{10}(f_c)-\frac{B}{A}}
}$$
逆に数dB上げたいとなると、B/Aを引き算ではなく足し算としたらよいだけです。
はい、本記事は以上になります。誰かの参考になれば幸いです。最後までお読みいただきありがとうございました!!!